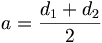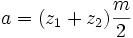Abwälzverfahren

Ein Zahnrad hat an seinem Umfang Zähne und Zahnlücken. Diese greifen in ein weiteres Bauteil (Rad oder Stange) mit dazu passenden Zähnen ein und übertragen die An- oder Abtriebskraft formschlüssig, das heißt ohne Schlupf. Der Eingriffspunkt soll abrollen, damit wenig Reibung und Verschleiß entsteht (Verzahnungsgesetz). Daher gleicht die Form der Zahnflanke entweder einer Evolvente oder einer Zykloide. Am weitesten verbreitet ist die Evolventenverzahnung.

Um eine ruckfreie Drehung beider Zahnräder zu erreichen, müssen immer mindestens zwei Zähne in Eingriff stehen.

Antriebsscheibe und Antriebsritzel mit Pfeilverzahnung der Merkur-Bergbahn von 1913 bis 1967

Animation eines Stirnradgetriebes. Nur eine der beiden Eingriffslinien ist hervorgehoben.

Allgemeines

Veränderung der Drehzahl und des Drehmoments

Zahnräder werden vor allem in Getrieben eingesetzt. Dazu werden sie auf Wellen oder Achsen gelagert bzw. so angebracht, dass ihre Zähne ineinander greifen und so die Drehbewegung des einen Zahnrades auf das andere übertragen werden kann. Dabei kehrt sich die Drehrichtung um, was ein gewünschter Effekt dieser Anordnung sein kann. Sind die Räder unterschiedlich groß, so kann entsprechend die Drehzahl erhöht bzw. verringert werden, wobei das Drehmoment vermindert bzw. erhöht wird. Auf diese Weise können Zahnräder auch der Übersetzung von Kräften und Geschwindigkeiten dienen.

Die Zahneingriffsfrequenz eines Zahnrades ergibt sich aus der Drehzahl mal Anzahl der Zähne.

Geschichte

Bei den altägyptischen Göpeln findet man die älteste Form des Zahnrades, ein Holzrad, in dessen Umfang man Pflöcke hineinstreckte. ^[1] Die Rolle war bereits bei den Assyrern in Gebrauch und wurde von den Ägyptern übernommen, die Verbindung dieser Rollen mittels Seil führte zum bekannten Flaschenzug. ^[2] Eine direkte Verbindung dieser Rollen wurde bereits 330 v. Chr. von Aristoteles erwähnt, gesichert ist die Anwendung von Zahnrädern bei Heron von Alexandria, überliefert durch Vitruv. Ktesibios verwendete um 250 v. Chr. an seiner Wasseruhr einen Stab, der mit Zahnrädchen besetzt war, ebenso Philon von Byzanz um 230 v. Chr. an zwei Apparaten Zahnräder. ^[3] Das heute bedeutendste Artefakt für die Anwendung von Zahnrädern in der Antike ist der Mechanismus von Antikythera von ca. 100 v. Chr.

Seit dem 9. Jahrhundert erfolgte in Europa der Einsatz von Zahnrädern in Wassermühlen, ab dem 12. Jahrhundert auch in Windmühlen. In Manuskripten Leonardo Da Vincis finden sich um 1500 Zahnräder in verschiedenen Anwendungen.

Georgius Agricola gab 1556 in seiner Schrift De re metallica libri XII erstmals den Einsatz von Zahnrädern aus Eisen an. ^[4] Anfangs wurde wenig auf die geeignete Form der Zähne geachtet. Nach Angaben von Christiaan Huygens und Gottfried Wilhelm Leibniz empfahl der dänische Astronom Ole Rømer um 1674 die Epi-Zykloïde als Zahnform. Vermutlich war er beim Bau seiner Planetarien, z.B. Jovilabium an der Pariser Academie des Sciences darauf gekommen. Schriftliche Belege dafür gibt es nicht mehr. Eine erste gründliche mathematische Untersuchung dieser Zahnräder beschrieb das Akademiemitglied Philippe de la Hire (1640-1718) um 1694 Traite des epicycloides (erschienen 1730). Diese epizykloidische Zahnform sichert eine gleichförmige Bewegung der Zahnräder bei gleichmäßiger Gleitreibung. Diese wurden gezielt in Uhrwerken eingebaut. 1759 entwickelte John Smeaton eine eigene Form, gefolgt von Leonhard Euler, der 1760 die Evolvente für die Zahnform vorschlug. Die Entwicklung der Dampfmaschine im 18. Jahrhundert führte zu einem steigenden Bedarf an Zahnrädern, da die zu übertragende Leistung kontinuierlich stieg und Zahnräder aus Metall anstatt wie bisher aus Holz gefertigt werden mussten. 1820 erfand Joseph Woollams die Schrägverzahnung und Pfeilverzahnung (Doppelschrägverzahnung) (englisches Patent Nr. 4477 vom 20. Juni 1820), James White baute 1824 daraus ein Differentialgetriebe. ^[5] 1829 stellte Clavet eine Zahnhobelmaschine her, da der Werkzeugmaschinenbau ab dem 19. Jahrhundert eine steigende Genauigkeit der Verzahnungen erforderte. Die erste brauchbare Maschine zum Fräsen geradverzahnter Stirnräder baute 1887 G. Grant. 1897 entwickelte H. Pfauter daraus eine universale Maschine, mit der sich auch Schnecken- und Schraubräder fertigen ließen. ^[6]

Arten von Zahnrädern

Stirnräder

Stirnräder

Das Stirnrad oder Zylinderrad ist ein einfaches Rad, das eine zylindrische Kontur hat und an seinem Umfang mit einer Verzahnung versehen ist. Die Achsen eines Stirnrades und seines Gegenrades (auch ein Stirnrad oder eine stirnverzahnte Welle) liegen parallel, es entsteht ein Stirnradgetriebe. Man unterscheidet Außen- und Innenzahnrad.

Das Stirnrad dient der Übertragung von Drehmomenten und der Veränderung von Drehzahlen. Die Aufnahme des Drehmomentes kann „von innen“ über den Sitz des Rades mittels der Mitnahme geschehen. Diese Mitnahme kann kraftschlüssig oder formschlüssig sein.

Die Aufnahme und auch Weitergabe des Drehmomentes kann, beispielsweise durch ein weiteres Zahnrad am Umfang erfolgen. In diesem Fall hat die Bohrung des Stirnrades eine reine Lagerungsfunktion. Diese Verwendung ist gelegentlich bei Rennmotoren (als Antrieb für die Nockenwelle) oder bei Zwischenrädern zu finden.

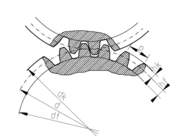
Die Verzahnung kann gerade, d. h. achsparallel, schräg (Schrägverzahnung) oder als Bogenverzahnung ausgeführt sein. Die Größe der Verzahnung wird bestimmt als Modul. Das Gegenrad muss eine Verzahnung von gleichem Modul aufweisen. Das Beispielfoto zeigt eine Pfeilverzahnung.

Kegelräder

Kegelräder

Hauptartikel: Kegelradgetriebe

Die Wellen stehen in einem Winkel (meist 90°) zueinander, müssen sich aber schneiden. Die Grundformen sind Kegel, deren Spitzen zusammenfallen. Nach der Zahnlängsform unterscheidet man geradverzahnte (Bild) und bogenverzahnte Kegelräder, bei letzteren wiederum solche mit Kreisbogen- und Epizykloidenform. Bogenverzahnte Kegelräder werden oft fälschlicherweise als spiralverzahnte Räder bezeichnet.

Hypoidverzahnung

Die Hypoidverzahnung ist Sonderbauart bei Kegelradgetrieben. Der Hypoid ist eine geometrische Kurve mit elliptischem Aussehen. Auf gleicher Zahnradbreite lässt sich so eine längere Zahnflanke unterbringen. Die Zahnflanken berühren sich nicht auf der gesamten Zahnfläche. Dadurch wird der Verschleiß minimiert, und das Getriebe läuft leiser. Nachteil: Höhere Drücke und Temperaturen erfordern ein Spezialöl.

Üblich ist die Hypoidverzahnung bei Kfz mit Hinterradantrieb im Differenzialgetriebe. Vorteil gegenüber spiralverzahnten Getrieberädern: die Achsen der beiden Zahnräder liegen nicht in der gleichen Flucht. Dadurch kann man die Antriebswelle tiefer in das Getriebegehäuse führen, wodurch Bauhöhe am Kardantunnel eingespart wird.

Schraubenräder

Schraubräder sind Schrägstirnräder, die auf sich kreuzenden Wellen sitzen. Normalerweise beträgt der Achswinkel 90°. Beim Abwälzen berühren sich Schraubräder jeweils nur in einem Punkt. Schraubräder können deshalb nur kleine Kräfte übertragen und werden vor allem für Steuerungszwecke verwendet.

Kronräder

Spindelrad (oben) und Kronrad.

Kron- oder Kronenräder sind Zahnräder, deren Lauffläche nicht wie bei den Stirnrädern die Stirnseite ist, sondern die Radfläche. Das Bild zeigt ein Kronrad, das ein Spindelrad (oben) antreibt, diese beiden Zahnräder sind gleichzeitig auch triebstockverzahnte Kammräder, da die Zähne einzeln gefertigt wurden.

Schnecke

Schneckengetriebe

Eine besonders häufig angewandte Form ist die Schnecke und das Schneckenrad, die zusammen das Schneckengetriebe bilden. Die beiden Achsen liegen hierbei windschief im Winkel von 90° zueinander. Die Schnecke ist quasi ein Zahnrad mit sehr kleiner Zähnezahl/Gangzahl (üblich z1 = 1-8), wobei die Zähne/Gänge schraubförmig um den Zylinder gewunden sind. Sie sind daher einer Schraube sehr ähnlich, wobei eine Windung einem Zahn entspricht. Das bedeutet, dass eine Umdrehung der Schneckenachse eine Schneckenradradteilumdrehung von 360°/z1 bewirkt. Daraus resultiert auch das Übersetzungsverhältnis von i=z2: z1. Unter einem bestimmten Steigungswinkelbereich der Schneckengänge werden Schneckengetriebe selbsthemmend, d. h. der Antrieb für die Übertragung einer Drehbewegung kann nur von der Schnecke auf das Zahnrad erfolgen, aber nicht umgekehrt. Ein Drehmoment welches vom Zahnrad auf die Schnecke wirkt, wird durch Reibungskräfte blockiert. In dieser Form werden Schneckengetriebe beispielsweise am Hebeseil von Kränen eingesetzt, so dass bei Ausfall des Antriebs die Last gehalten wird.

Sonderformen

Zahnräder sind im Allgemeinen kreisrund, es gibt jedoch auch Ausnahmen.

Zahnstangen

Leonardo da Vinci, Schloss Clos Lucé bei Amboise

Zahnstangen sind gerade Stangen. Sie ermöglichen eine Umwandlung einer Rotation in eine lineare Bewegung und umgekehrt. Die Bewegungsfreiheit ist jedoch eingeschränkt, da die Stange in der Länge begrenzt ist und somit nur eine abwechselnde Bewegung in die zwei entgegengesetzten Richtungen längs zur Stange zulässt. Eine mögliche Anwendung ist die Zahnradbahn.

Elliptische Zahnräder

Dabei müssen beide Räder zueinander genau abgestimmt werden, damit die beiden Wellen einen konstanten Abstand während der ganzen Drehung haben. Der Sinn ist der, dass sich während einer Umdrehung das Übersetzungsverhältnis ändert. Der Drehmittelpunkt der beiden Räder liegt jeweils genau in der Mitte der beiden Brennpunkte. Ist nur ein Rad elliptisch, so muss ein Rad auf einer Schwingachse laufen. Verwendet wurden solche Zahnräder bei Webmaschinen zum Festschlagen der Gewebe und heute beim vorderen Kettenblatt von einigen Fahrrädern.

Verzahnungsarten bei Stirnrädern

Evolventenverzahnung

L-Verzahnung (keine Evolventenverzahnung)

Hauptartikel: Evolventenverzahnung

• Verwendung: beim Antrieb vom Schnellen ins Langsame oder umgekehrt (z. B. Auto, Maschinenbau)
• leichte Normierung
• Räderpaare können bei gleicher Reibung links- und rechtsherum angetrieben werden
• relativ spielarme Verzahnung
• unempfindlich gegenüber Achsabstandsänderung, da die Eingriffslinie eine Gerade ist
• im Wälzpunkt ausschließlich Rollreibung; vom Wälzpunkt weggehend zunehmend Gleitreibung
• durch die konvexe Zahnform entsteht eine hohe Flächenpressung, was einen Nachteil hinsichtlich der Lebensdauer bedeutet.
• Herstellung der Zahnräder relativ einfach und kostengünstig

Zykloidenverzahnung

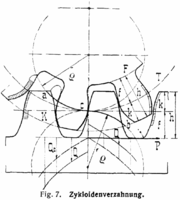
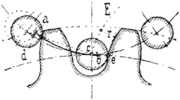
Zykloidenverzahnung

• Verwendung: Beim Antrieb vom Langsamen ins Schnelle (z. B. bei mechanisch angetriebenen Uhren).
• Bei einem Antrieb vom Langsamen ins Schnelle besteht eine geringere Reibung als bei Evolventenverzahnung.
• Größere Übersetzungsverhältnisse auf kleinem Raum sind möglich, da die Zähne am Fuß schmaler sind als bei der Evolventenverzahnung.
• Reine Rollreibung erst ab einer bestimmten Zähnezahl des kleineren angetriebenen Rades möglich.
• Normierung schwierig, da die Zahnform gegenüber der Evolvente zusätzlich von der Zähnezahl des kleineren angetriebenen Rades abhängt. Man muss also um ideale Eingriffs- und Reibungsverhältnisse zu bekommen, die Zähne eines Räderpaares speziell zueinander konstruieren. In der Uhrmacherei wurden Normierungskompromisse unternommen.
• Kein Vorwärts-Rückwärtslauf möglich. Das heißt Drehbewegung nur in einer Richtung sinnvoll möglich.
• Größeres Zahnspiel (staubverträglicher).
• Geschmiert werden nur die Radlager, die Räder selbst werden trocken betrieben um Schmutzansammlung zu vermeiden.
• die Eingriffstiefe ist kritischer als bei der Evolventenverzahnung. In der Uhrmacherei reicht der mathematisch ermittelte Abstand als Ideal nicht aus. Er wird zusätzlich empirisch angepasst (muss erfühlt werden).

Wildhaber-Novikov-Verzahnung

• Verwendung: in Stirnverzahnungen (Laufverzahnungen).
• Konvexe, halbkreisförmige Zähne greifen in gleichartig ausgebildete konkave Lücken ein. Der theoretische Radius von Zahn und Zahnlücke ist gleich, in der Praxis wird der Zahnlückenradius etwas größer ausgeführt.
• Es kann keine Profilüberdeckung realisiert werden, für eine gleichmäßige Bewegungsübertragung ist eine Schrägverzahnung mit einer Sprungüberdeckung >1 erforderlich. Der Eingriffswinkel ist in jeder Zahnstellung konstant, so dass die Zahnkraft ihre Richtung nicht ändert.
• Vorteilhaft wirkt sich die konstruktionsbedingte gute Schmiegung von Zahn und Zahnlücke aus. Weitere Vorteile liegen in der guten Tragfähigkeit (höher als Evolventenverzahnung), im gleichmäßigen Verschleiß (geringe Relativbewegung der Flanken zueinander) und im günstigen Geräusch- und Schwingungsverhalten.
• Kritisch ist diese Verzahnung bei geometrischen Abweichungen wie Teilungs- und Zahnrichtungsfehlern sowie bei Achsabstands- und Achsneigungsabweichungen.
• Der Herstellungsaufwand ist groß, da für Rad und Gegenrad verschiedene Verzahnwerkzeuge erforderlich sind.

Konchoidenverzahnung

Konchoidenverzahnung

• Verwendung: z. B. bei Zahnstangen

Triebstockverzahnung

Ritzel einer Triebstockverzahnung

Triebstockverzahnung

• Verwendung: z. B. alte Mühlenräder, Schwarzwälder Uhren, Zahnstangen, Rollenketten
• Anwendung weitgehend durch die Evolventen- und Zykloidenverzahnung verdrängt. Frühere Vorteile dieser Verzahnung war die leichtere Herstellung von Rädern. Außerdem war eine ausreichend genaue Teilung mittels einer Bohrschablone leicht zu erreichen.

Die Verzahnung kann gerade, d. h. achsparallel, schräg (Schrägverzahnung) oder als Bogenverzahnung ausgeführt sein. Die Größe der Verzahnung wird bestimmt als Modul. Das Gegenrad muss eine Verzahnung von gleichem Modul aufweisen.

Bestimmungsgrößen von Geradstirnrädern

Zahnradpaar im Eingriff, Zahnrad mit 24 Zähnen, Modul = 2 mm, Teilkreisdurchmesser d = 48 mm, Kopfkreisdurchmesser dk = 52 mm

Zwei Durchmesser sind für die Bestimmung eines Zahnrades mit geraden Flanken wichtig: der Außen- und der Arbeitsdurchmesser. Der Außendurchmesser bestimmt den Platzbedarf des Zahnrades. Der Arbeitsdurchmesser bestimmt den Abstand der Zahnradachsen. In der Fachliteratur wird der Außendurchmesser als Kopfkreis-Durchmesser und der Arbeitsdurchmesser als Teilkreis-Durchmesser bezeichnet. Der Teilkreis wird in technischen Zeichnungen mit strichpunktierter Linie dargestellt.

Die Teilung p des Zahnrads ist der Abstand von Zahnmitte zu Zahnmitte auf dem Teilkreisdurchmesser. Der Modul m ist das Verhältnis der Teilung p zur Zahl Pi, m = p/π.

Der Durchmesser des Teilkreises ergibt sich aus dem Produkt von Modul und Zähnezahl z, d = m · z. Rad und Gegenrad müssen immer den gleichen Modul besitzen. Die Kopfhöhe der Zähne ist gleich dem Modul, ha = m. Die Fußhöhe ist gleich dem Modul plus Spiel; üblich sind 25 Prozent vom Modul Spiel, h_f = 1,25 · m. Der Kopfkreisdurchmesser d_a ist gleich d_a = m · (z + 2). Der Fußkreisdurchmesser d_f ist d_f = m · (z - 2.5). (Diese Formeln gelten nur für geradverzahnte Zahnräder ohne Profilverschiebung, d.h. unkorrigierte Zahnräder).

Der Achsabstand a zweier Geradstirnräder 1 und 2 lässt sich mit den folgenden beiden Formeln berechnen:

$a = \frac{d_1 + d_2}{2}$

$a = (z_1 + z_2) \frac{m}{2}$

Der Modul bei Stirnrädern ist gemäß DIN 780-1 zu wählen.

Prüfen von Zahnrädern

Allgemeines

Die Prüfung von Zahnrädern ist sehr umfangreich und richtet sich nach der Art des Zahnrades. Bei der Zahnradprüfung werden die verschiedenen Bestimmungsgrößen von Zahnrädern mittels konventioneller Längen- und Winkelmessverfahren und spezieller Zahnradmessverfahren ermittelt.

Prüfen von Kegelrädern

Die Prüfung von Kegelrädern erfolgt hauptsächlich durch Laufprüfung. Unter Verwendung einer Laufprüfmaschine wird das zu prüfende Kegelrad mit einem Meisterrad in Eingriff gebracht und bei Sollachsabstand, Sollachswinkel und Solldrehzahl abgewälzt. Es wird eigentlich die spätere Funktion im Getriebe simuliert.

Die Qualität des Kegelrades wird durch das entstandene Tragbild, die Geräuschentwicklung während der Laufprüfung und das Verdrehflankenspiel beurteilt.

Bei den Laufprüfungen unterscheidet man zwischen Zweiflankenwälzprüfungen und Einflankenwälzprüfungen.

Ergänzende Prüfungen sind weiterhin die Rundlaufprüfung durch Rundlaufprüfgeräte und die Zahndickenprüfung mit Zahndickenmessgeräten. Die rasante Entwicklung der Prüfmethoden ist auch bei der Kegelradprüfung erkennbar. Die Verwendung von Koordinatenmessgeräten hat inzwischen auch auf die Kegelradprüfung großen Einfluss. Mit entsprechender Software wird die Topografie des Kegelrades ermittelt, das Tragbild und Verdrehflankenspiel berechnet und simuliert. Korrekturwerte werden direkt an die Verzahnmaschine weitergeleitet.

Prüfen von Stirnrädern

Grundlage für die Prüfung von Stirnrädern ist die DIN 3960/3961.

Abhängig von den Qualitätsansprüchen gibt es unterschiedliche Prüfverfahren. Bei der Zweiflankenwälzprüfung wird der Prüfling mit einem beweglich gelagerten Lehrzahnrad spielfrei in Eingriff gebracht und abgewälzt.

Die entstehenden Achsabstandsänderungen werden registriert und als Zweiflankenwälzabweichung und Zweiflankenwälzsprung ausgewertet. Dabei werden nur Summenabweichungen ermittelt, d. h. Fehlerursachen sind teilweise schwer erkennbar. Das Lehrzahnrad muss geometriebezogen mit dem Prüfling übereinstimmen. Für Zahnräder mit hohen Qualitätsanforderungen ist dieses Verfahren weniger geeignet. Die Wälzprüfung kann hervorragend in Fertigungsabläufe integriert werden. Vergleichbar mit der Zweiflankenwälzprüfung ist das Verfahren der Einflankenwälzprüfung. Vorteilhaft bei diesem Prüfverfahren ist die Zuordnung der Abweichungen zur Rechts- bzw. Linksflanke. Die Ermittlung der Einzelfehler eines Stirnrades ist die sicherste und genauste Methode zur Qualitätsbestimmung.

Mit Koordinatenmessmaschinen und entsprechender Software werden die Profil-, Flanken- und Teilungsabweichungen sowie die Zahnweite ermittelt und im Messprotokoll ausgewertet. Dieser Messvorgang erfolgt automatisch. Dabei wird die Qualität des Zahnrades eindeutig definiert. Eine gezielte Korrektur der Bearbeitungsmaschine ist möglich.

Die Zahndickenprüfung erfolgt durch Zahnweitenbügelmessschrauben.

Herstellung

Wälzfräsen an einem horizontalen Zahnrad

Die Herstellung von Zahnrädern kann prinzipiell auf drei Arten erfolgen

• Urformend (Gießen, Sintern)
• Umformend (Schmieden, Pressen, Ziehen, Walzen, Stanzen)
• Spanend (s. u.)

Ur- und umformende Verfahren werden meist für weniger stark belastete Zahnräder eingesetzt, diese Verfahren lassen sich häufig kostengünstig umsetzen (z. B. Gießen oder Ziehen von Kunststoffzahnrädern, Sintern oder Stanzen bei Metallzahnrädern, bei denen es nicht auf große Genauigkeit ankommt). Spanende Verfahren kommen bei hochbelasteten Zahnrädern zum Einsatz, hier lassen sich auch größere Genauigkeiten erzielen (wichtig wenn es z. B. auf geräuscharmen Lauf oder kleines Verdrehflankenspiel ankommt).

Wälzfräsmaschine

Die wichtigsten spanenden Verfahren sind:

• mit geometrisch bestimmter Schneide
  • Wälzhobeln
  • Abwälzfräsen
  • Wälzfräsen, Profilfräsen
  • Wälzstoßen
  • Wälzschälen
  • Profilräumen
  • Schaben
• mit geometrisch unbestimmter Schneide
  • Wälz- oder Profilschleifen
  • Honen
  • Läppen

Beim Profilfräsen oder -schleifen hat schon die Werkzeugschneide die exakte Form der Zahnflanke. Bei Wälzverfahren wird ein Werkzeug mit zumeist gerader Schneide von der Herstellungsmaschine so geführt, dass es mit der herzustellenden Zahnflanke „abwälzt“. Der Materialabtrag erfolgt nur an einem Punkt bzw. auf einer Linie. Hier kann ein Werkzeug für viele verschiedene Verzahnungsgeometrien genutzt werden, die Kinematik und somit die Steuerung der Maschine ist aber relativ kompliziert. Beim Profilverfahren benötigt man eine große Anzahl verschiedener Werkzeuge oder muss die Schleifscheibe vor ihrem Einsatz erst in die Form der Zahnflanke bringen („abrichten“ der Schleifscheibe). Wälzverfahren können kontinuierlich erfolgen, d. h. das ganze Zahnrad kann in einer durchgehenden Bewegung gefertigt werden (z. B. durch einen schneckenförmigen Fräser). Profilverfahren arbeiten immer im Teilverfahren, es kann also nur jeweils eine Zahnlücke gefertigt werden, danach wird das Werkrad um eine Lücke weitergedreht.

Zahnräder werden nach dem Verzahnen i. d. R. gehärtet. Die Oberfläche wird dadurch verschleißfester und das Zahnrad kann höhere Belastungen ertragen. Allerdings entsteht beim Härten Härteverzug, deshalb müssen in der Regel die Flanken nach dem Härten nachbearbeitet werden um die Verzahnungsqualität zu verbessern.

Eine weitere Bearbeitungsmöglichkeit ist das Erodieren. Kleine Zahnräder werden auch geätzt (ähnlich Lithographie) oder galvanisch hergestellt.

Verzahnungsqualitäten

Es existieren 12 Verzahnungsqualitäten, die unterschiedlich gefertigt werden, wobei 1 die feinste und 12 die gröbste Verzahnungsqualität ist.

Fertigungsverfahren:

• Qualität 1-6 gehont
• Qualität 2-7 geschliffen
• Qualität 5-7 geschabt
• Qualität 5-9 wälzgefräst, wälzgehobelt, wälzgestoßen
• Qualität 7-12 formgefräst, formgestoßen
• Qualität 8-12 gestanzt, gepresst, gesintert, gespritzt

Schadensarten

Folgende Schäden können auftreten:

• Grübchenbildung (Pitting)
• Zahnbruch, meist im Bereich des Zahnfußes
• Graufleckigkeit (Micro-Pitting)
• Fressen
• Verschleiß (bei Langsamlauf)

Siehe auch

• Planetenradgetriebe
• Sperrklinke
• Der Hypoidantrieb ist ein spezielles Kegelradgetriebe.
• Als Zahnräder werden auch das Kettenblatt und die Ritzel eines Fahrrades bezeichnet, zu den Besonderheiten dieser Art der Kraftübertragung siehe Kettengetriebe
• Mechanismus von Antikythera
• Duplex-Schnecke, die spieleinstellbare Variante der Schneckenverzahnung
• Evolventenverzahnung
• Trieb (Uhrwerk)

Einzelnachweise

1. ↑ Albert Neuburger: Die Technik des Altertums. R. Voigländer Verlag Leipzig. 4. Auflage 1919. Seite 221
2. ↑ Albert Neuburger: Die Technik des Altertums. R. Voigländer Verlag Leipzig. 4. Auflage 1919. Seite 212
3. ↑ F.M. Feldhaus: Die Technik. R. Löwit Verlag Wiesbaden. 1914. Seite 1341
4. ↑ F.M. Feldhaus: Die Technik. R. Löwit Verlag Wiesbaden. 1914. Seite 1345
5. ↑ F.M. Feldhaus: Die Technik. R. Löwit Verlag Wiesbaden. 1914. Seite 1347
6. ↑ Deutsches Museum: Zahnrad-Wälzfräsmaschine

Literatur

• Linke, Heinz: Stirnradverzahnung. Hanser Verlag, München 1996, ISBN 3-446-18785-5.
• Basler Zeitung vom 1. Dezember 2006, S. 40: High Tech aus der griechischen Antike
• King, Henry C.: Geared to the Stars - planetaries, orreries and clocks , Toronto 1978

Weblinks