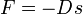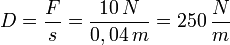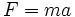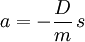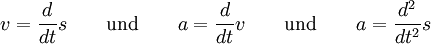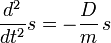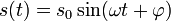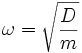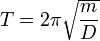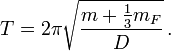Federschwinger

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Ein Federpendel

Ein Federpendel oder Federschwinger ist ein aus einer Feder und einer Masse bestehendes schwingungsfähiges System.

Beim Federpendel hängt ein Massestück an einer Schraubenfeder oder einem Gummiband und führt nach einer entlang der Federachse gerichteten Anregung eine harmonische Schwingung aus. Ist die Feder linear, hat die Schwerkraft keinen Einfluss auf die Resonanzfrequenz.

Die Schraubenfeder erzeugt ihre Federkraft aufgrund der Torsion im Federdraht, dennoch handelt es sich beim Federpendel nicht um ein Torsionspendel - jenes führt eine Drehschwingung aus.

Zu sich drehenden Federschwingern siehe:

• Torsionspendel (Drehpendel): Federkraft entsteht durch Torsion in einem gestreckten Draht oder einem Band
• Unruh (Uhr), Drehschwinger mit Spiralfeder: Federkraft entsteht durch Biegung in der Spiralfeder

Herleitung der Schwingungsgleichung

Bewegung eines Federpendels

Die elastische Auslenkung einer idealen Feder, d. h. einer masselosen und reibungsfreien Feder, ist durch das vereinfachte Hookesche Gesetz beschrieben:

$\, F = -D s$

Eine lineare Torsions- oder Schraubenfeder übt eine entgegen der Auslenkung (Dehnung) s gerichtete, zu s proportionale Kraft F aus. Die Proportionalitätskonstante D wird Federkonstante genannt, das Minuszeichen besagt nur, dass Kraft- und Dehnungsrichtung entgegengesetzt sind. Beispiel: Eine Feder ist zunächst 20 cm lang. Durch Anhängen eines Massenstückes von 1 kg (Gewicht 10 N) wird sie auf 24 cm Länge gedehnt. Daraus errechnet sich der Wert der Federkonstanten

$D=\frac{F}{s}=\frac{10\,N}{0,04\,m}=250\,\frac{N}{m}$

Wenn an der aktuellen Feder eine Masse m befestigt ist, so wirkt die Federkraft nach dem zweiten Newtonschen Gesetz beschleunigend auf diese Masse:

$\, F = m a$

wobei a die Beschleunigung bezeichnet. Sowohl die Kraft als auch die Dehnung ändern sich als Funktion der Zeit t und es geht nun darum, eine dieser beiden Größen zu ersetzen, um eine einzige Gleichung für nur eine Unbekannte zu erhalten. Üblicherweise eliminiert man aus den beiden Gleichungen die Kraft und es ergibt sich die Bewegungsgleichung

$a = -\frac{D}{m} \, s$

mit den beiden unbekannten Funktionen a und s. Beschleunigung, Geschwindigkeit und Weg sind aber nicht unabhängig voneinander, sie sind über folgende Formeln miteinander verknüpft:

$v=\frac{d}{dt}s \qquad \text{und} \qquad a=\frac{d}{dt}v \qquad \text{und} \qquad a=\frac{d^2}{dt^2}s$

Die Geschwindigkeit ist die erste Ableitung der Auslenkung nach der Zeit und die Beschleunigung die zweite Ableitung der Auslenkung nach der Zeit. Damit ergibt sich die Differentialgleichung des harmonischen Oszillators:

$\frac{d^2}{dt^2} s = -\frac{D}{m} \, s$

In Worten: Man sucht eine Funktion s, deren zweite Ableitung das entgegengesetzte Vorzeichen besitzt und sich um den Faktor D/m von der Funktion unterscheidet. Es existiert eine Lösung

$s(t) = s_0 \sin( \omega t + \varphi)$

die als die Schwingungsgleichung (periodische Bewegung) des Massenpunktes um die Ruhelage s=0 bezeichnet wird. Die Ruhelage ist beim Federpendel durch die gegenseitige Aufhebung von Gewichtskraft der Masse und Rückstellkraft der Feder gekennzeichnet (Gleichgewichtslage). Die Lösungsparameter s₀ (Amplitude) und φ (Phase) bestimmen sich aus den Anfangsbedingungen, während sich die Kreisfrequenz ω aus Masse und Federkonstante gemäß

$\omega = \sqrt{\frac{D}{m}}$

herleitet. Sie hängt mit der Schwingungsdauer T des Federpendels über 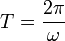$\,T=\frac{2\pi}{\omega}$ zusammen. Somit beträgt die Schwingungsdauer

$T = 2\pi \sqrt{\frac{m}{D}}$

Setzt man das oben begonnene Beispiel fort, erhält man die Ergebnisse ω = 15,8 1/s, T = 0,4 s und s₀ = 4 cm.

Anmerkungen

Die aufgeführten Gleichungen beschreiben das reale Federpendel nur näherungsweise.

1. Die innere Reibung der Feder führt zu einer Abbremsung der Schwingung. Man spricht dann von einem gedämpften harmonischen Oszillator oder einer gedämpften Schwingung.
2. Die Feder selbst besitzt auch eine Masse, die zu beschleunigen ist. Die Schwingungsdauer wird bei Berücksichtigung der Federmasse m_F zu

$T = 2\pi \sqrt{ \frac{m + \frac{1}{3}m_F}{D}} \, .$

Das Gravitationfeld der Erde wirkt sich über die Gewichtskraft der Masse nur auf die Position der Ruhelage aus (bei Näherung g(s) = konst.). Es hat im Übrigen keine Auswirkung auf das Schwingverhalten, welches allein durch die Trägheit der Masse und die Federkonstante bestimmt wird.

Siehe auch

• Mathematisches Pendel (Fadenpendel)
• Magnetisches Pendel
• Torsionspendel
• Unruh (Uhr)
• Spannenergie

Weblinks

• Animiertes Federpendel (Java-Applet) mit Darstellung von allen periodischen Größen