Altersstruktur

Prognostizierte Altersverteilung für Deutschland im Jahr 2050

Als Altersstruktur oder Altersverteilung wird die statistisch altersmäßige Verteilung, in Gruppen von Personen zum Erfassungszeitpunkt, sowie, bei - dazu spezifizierten - Gebrauchsgegenständen, z.B. von Pkws, Waschmaschinen, Computern usw., bezeichnet. Im allgemeinen Sprachgebrauch ist mit Altersstruktur fast immer die Altersverteilung der Bevölkerung gemeint. Die grafische Darstellung dieser Verteilung wird auch als Alterspyramide oder Bevölkerungspyramide bezeichnet, wobei die Altersstruktur getrennt nach Frauen und Männern auf zwei Seiten dargestellt wird. Eine solche Grafik ist wie folgt aufgebaut (siehe Beispiel rechts):

• X-Achse: Anzahl oder Anteil Menschen zu einem Jahrgang (Lebensalter)
• Y-Achse: Lebensalter der Menschen
• Durch die Anordnung der Y-Achse in der Mitte der X-Achse werden in die eine Richtung der X-Achse die Anteile der Frauen und in die andere Richtung der X-Achse die Anteile der Männer dargestellt.

Aus dieser Anordnung der Achsen und Werte entstehen verschiedene grafische Formen, die in ihrer Entstehung und in den sozialen Auswirkungen unterschiedlichste Ursachen und Ergebnisse haben.

Der Begriff Alterspyramide ist aus den ersten derartigen Darstellungen entstanden, die pyramidenförmig aussehen, da hier die jüngsten Jahrgänge, die die Basis der Grafik bilden, die meisten Vertreter stellen und die Zahl der Angehörigen eines Jahrgangs mit zunehmendem Alter abnimmt. Auch wenn sich in den allermeisten Industriestaaten die Altersstruktur aufgrund der verringerten Sterblichkeit (Mortalität oder Sterberate), der gestiegenen Lebenserwartung und der gesunkenen Geburtenrate schon längst von der ursprünglichen Alterspyramide weg entwickelt hat (Begriff der so genannten Überalterung), wird dieser Begriff allgemein verwendet. In Entwicklungs- und Schwellenländern findet sich teilweise noch heute die namensgebende Pyramidenform.

Entsprechend der Geschichte einer Bevölkerung sind bestimmte grafische Formen als Ergebnis zu erwarten. Dabei sorgen unterschiedliche Ereignisse in der Entwicklung der Bevölkerung für erkennbare Veränderungen oder Verformungen. Beispiele hierfür sind Kriege, Naturkatastrophen und Veränderungen im kulturellen und sozialen Verhalten der Menschen (zum Beispiel ‚Pillenknick‘).

Das Durchschnittsalter der Weltbevölkerung im Jahr 2009 beträgt gemäß dem World Factbook der CIA 28,4 Jahre^[1].

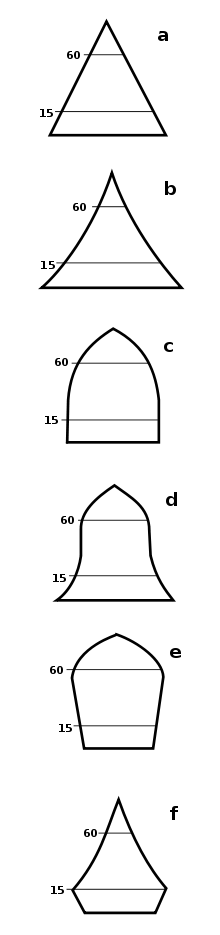
Typische Formen der Altersstrukturen

Die sechs Grundformen der Altersstruktur^[2][3][4]

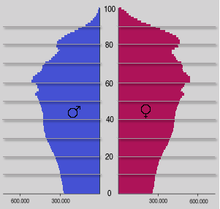
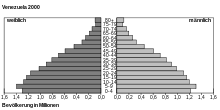Bevölkerungspyramide Venezuelas – klassische Pyramidenform

a) Lineare oder klassische Pyramidenform (gleichschenkelige Dreiecksform)

Ein nahezu lineares Abnehmen der Bevölkerungszahl je Altersgruppe mit steigendem Alter ergibt sich aus vielen geborenen Kindern und einer dauerhaft hohen Sterblichkeit über alle Altersstufen hinweg, das heißt die Lebenserwartung aller Neugeborenen ist niedrig, oder eine nur leicht abnehmende Kinderzahl pro Frau, die aber trotzdem über 2,1 liegt. Diese Form der Pyramide ist verbreitet in Südamerika und Indien, aber auch in christlich-konservativ geprägten Countys der USA (Holmes County, Ohio). Um das Jahr 1890 lag auch in Deutschland und Österreich diese Struktur vor.

b) Verbreiterte bzw. modifizierte Pyramidenform (Pagodenform)

Bei einer konstant sehr hohen oder sogar steigenden Geburtenrate besitzt die Pyramide eine sich nach unten exponentiell verbreitende Basis. Dies geht einher mit einer meist geringen Lebenserwartung und einer früh einsetzenden, hohen Sterberate über alle Lebensalter hinweg, falls diese Pyramide ein Entwicklungsland beschreibt. Solche Pyramidenformen sind üblich in Afrika und anderen ärmsten Staaten.

c) Bienenstockform

Die Bienenstockform entsteht aus einer langsam zusammenlaufenden Altersstruktur, die sich im hohen Alter abrupt zusammenzieht. Sie gilt als Ideal, da die Bevölkerungszahl weder steigt noch sinkt. Voraussetzungen hierfür sind, dass eine höhere Lebenserwartung besteht, eine spät einsetzende, hohe Sterberate vorliegt und die Geburtenrate nahezu konstant auf dem Ersatzniveau von 2,1 Kindern pro Frau ist. Falls die Kinderzahl konstant bleibt, werden die USA diese Form in naher Zukunft erreichen.

d) Glockenform

Diese Form ist charakteristisch für eine Bevölkerung die nach längerer Zeit mit niedrigen Fertilitäts- und Mortalitätsraten wieder mit einer steigenden Geburtenhäufigkeit konfrontiert wird. Ein Beispiel für diesen Alterspyramidentyp wären die Industriestaaten um 1960, zur Zeit des Babybooms.

Bevölkerungspyramide von München – Mischform zwischen Zwiebelform und Tannenbaumform

e) Zwiebelform oder Urnenform (überspitzte Zwiebelform)

Viele Industriestaaten weisen diese Form der Altersstruktur auf, da hier eine niedrige Geburtenrate im Übergang zu einem Überhang älterer Menschen führt. Gleichzeitig nehmen die jüngeren Jahrgänge jeweils von Jahr zu Jahr ab. Dieses Phänomen wird meist als Überalterung bezeichnet. Voraussetzungen sind die bei unter 2,1 Kindern pro Frau liegende Geburtenrate, eine hohe Lebenserwartung mit einer erst spät einsetzenden, hohen Sterberate. Die altersspezifische Mortalität bleibt allerdings gleich. Alterspyramiden ökonomisch hoch entwickelter Staaten, wie jene des heutigen Westeuropas können in der Regel diesem Typ zugeordnet werden.

f) Tannenbaumform

Die Tannenbaumform besteht aus einem sehr schmalen Stamm in den jungen Altersgruppen, der ab den 20-Jährigen massiv breiter wird und ab den etwa 35–40-Jährigen sich langsam zusammenzieht. Die größten Altersgruppen sind die 25–30-Jährigen. Vor allem in Industriestaaten besitzen Großstädte und insbesondere die Innenstädte dieser Großstädte tannenbaumförmige Bevölkerungspyramiden. Das hängt damit zusammen, dass die innerstädtischen Bezirke wenig für Familien und ältere Leute, dafür aber für junge Erwachsene sehr attraktiv sind. Besonders stark ausgeprägt ist die Tannenbaumform in Universitätsstädten oder Szenevierteln, wie Shibuya, Friedrichshain-Kreuzberg oder Manhattan.

Die Übergänge zwischen diesen Formen sind fließend, jedoch können sie aus den kulturellen und sozialen Gegebenheiten der betrachteten Bevölkerung vorhergesagt werden. Auch wenn der Entwicklungsstand eines Landes nicht dem demographischen Stand gleichzusetzen ist, lässt sich durch die Form der Altersstruktur dieser oft erahnen. Ist der prozentuale Anteil der Unter-20-Jährigen größer oder gleich 50 % so spricht man in der Regel von einem Entwicklungsland.

Die typische Reihenfolge ist:  $a) \xrightarrow\ b) \xrightarrow\ f) \xrightarrow\ c) \xrightarrow\ e)$^[4]

Siehe auch Hauptartikel: Demografischer Übergang

Zu beachten ist, dass die Formen e) und f) nicht stabil sind, d. h. auf Dauer können diese Strukturen nicht erhalten sein. Die Struktur entwickelt sich in eine andere, stabile Form weiter; im Extremfall mit einer Geburtenrate von Null.

Abschätzung der Altersverteilungen

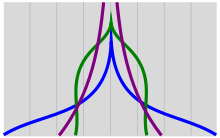
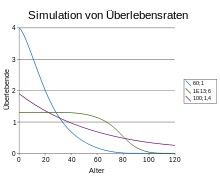Weibull-simulierte Altersverteilungsfunkionen mit auf 100 normiertem Flächeninhalt

Die beobachtete Altersstruktur lässt sich durch unterschiedliche Verteilungsfunktionen annähern.

Ein erster Ansatz, die Altersverteilung mit nur einem Parameter, der Mortalität, zu beschreiben, ist die Exponentialverteilung. Wenn eine Population die Größe von B Personen hat, und F(x) die Zahl der Verstorbenen in Abhängigkeit des Alters angibt, dann ist B − F(x) = S(x) die Zahl der noch Lebenden. Die Altersverteilung S lautet demnach:

$S(x)= const * e^{-m \cdot x}$ mit m: Mortalität.

Die Konstante wird so gewählt, dass die Summe über S(x) gerade die Population B ergibt.

Der Erwartungswert der Exponentialverteilung ist der Kehrwert der Mortalität, der Lebenserwartungswert $\tfrac 1m$. Für die Beispiele oben beträgt er für Deutschland $\tfrac 1{0{,}01044}\approx 96$ Jahre, für Mexiko 211 Jahre, für China 144 Jahre und für Russland 65 Jahre. Die hohen Werte für Mexiko und China resultieren aus dem hohen Anteil junger Menschen aufgrund des Bevölkerungswachstums. Die Exponentialverteilung kennt keine Alterung, weshalb sie unrealistisch hohe Lebensalter zulässt.

Ein verbesserter Ansatz modelliert die Verteilung mit einer altersabhängigen Mortalitätsrate m(x):

$m \rightarrow m(x)= m_0 \cdot x^{b-1}.$

Eingesetzt in die Verteilungsfunktion S(x) ergibt sich die Weibull-Verteilung mit den beiden Parametern m₀ und b:

$S(x)= e^{-m_0 \cdot x^b}.$

Das Diagramm zeigt eine Altersverteilung für die Exponentialverteilung und zwei für die Weibull-Verteilung. Die Parameter sind in der Tabelle zusammengestellt. Die Gesamtzahl (Flächenintegral) beträgt bei allen drei Kurven 100 (beispielsweise 100 Mio. Menschen).

Kurvenparameter des Diagramms

Kurve		$\tfrac 1{m_0}$	b		$\tfrac 1{m(1)}$	$\tfrac 1{m(20)}$	$\tfrac 1{m(50)}$	$\tfrac 1{m(80)}$		S(1)	S(60)	S(90)
1		60	1,0		60	60	60	60		1,9	0,7	0,5
2		100	1,4		100	30	21	17		4,0	0,2	0,04
3		1013	6,8		1013	3·105	1400	91		1,3	1,2	0,2

• Kurve 1 ist eine Exponentialverteilung mit einem Lebenserwartungswert unabhängig von der Zeit. Für die Jahre 1, 20, 50 und 80 beträgt er konstant 60 Jahre. Der Anteil der Einjährigen Personen beträgt 1,9 (also hier 1,9 Millionen), der der 90-Jährigen 0,5.
• Kurve 2 besitzt einen Lebenserwartungswert von $\tfrac 1{m_0}=100$ mit der Konstanten b = 1,4. Daraus folgt eine Altersabhängigkeit von $\tfrac 1{m(x)}$, die von 100 Jahren bei einem Lebensalter von einem Jahr auf 17 Jahre bei einem Alter von achtzig fällt. Die Verteilung ist pyramidenförmig.
• Kurve 3 simuliert eine konstante Verteilung mit einem Abfall bei sechzig Jahren durch einen sehr hohen Lebenserwartungswert von 10¹³ bei einem Lebensalter von einem Jahr, der auf Grund des großen Werts von b = 6,8 mit zunehmenden Alter sehr schnell abfällt.

Kurve um 90° gedreht

Um die Kurven mit einer Alterspyramide zu vergleichen, sind sie um 90° nach links zu drehen, so dass das Lebensalter zur Ordinate wird.

Führt man weitere Parameter ein, lassen sich die beobachteten Werte genauer wiedergeben. Andererseits wird die Interpretation der Bedeutung der Parameter schwieriger.

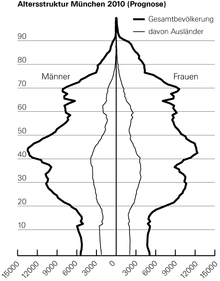
Land	Rohe Sterberate	Mittlere Lebenserwartung bei Geburt	Grundform Alterspyramide
Deutschland (2008)	10,80/1000	79,01 Jahre	Urnenform
Mexiko (2008)	4,78/1000	75,84 Jahre	Pyramidenform
China (2008)	7,03/1000	73,18 Jahre	Bienenstockform
Russland (2008)	14,62/1000	67,88 Jahre	Urnenform

Siehe auch

• Demografie
• Bevölkerungsentwicklung
• Lebenserwartung
• In den
   Commons: Alterspyramiden – Sammlung von Bildern, Videos und Audiodateien
  finden sich die nationalen Alterspyramiden vieler Länder für 2005 und die Deutsche für 1975 („Pillenknick“).

Weblinks

 Commons: Alterspyramiden – Sammlung von Bildern, Videos und Audiodateien

• Berlin-Institut für Bevölkerung und Entwicklung
• Statistisches Bundesamt Deutschland - Alterspyramide 1950-2060, 12. koord. Bevölkerungsvorausberechnung
• Statistik Österreich - Bevölkerungspyramiden (Excel)
• Österreich 1991 - dynamische Excel-Bevölkerungspyramide der Uni Klagenfurt

Einzelnachweise

1. ↑ Median age online beim World Factbook der CIA; Stand: 17. Mai 2010. (englisch)
2. ↑ Bähr, J., C. Jentsch, W. Kuls, 1992, Bevölkerungsgeographie. (= Lehrbuch der Allgemeinen Geographie, Bd. 9). – New York, Stuttgart, S. 177–181. online bei Google Book Search. Stand: 30. Januar 2009
3. ↑ Kuls, W., 1980, Bevölkerungsgeographie. Eine Einführung. – Stuttgart. S. 65.
4. ↑ ^{a b} Husa K. und H. Wohlschlägel, 2007, Proseminar Grundzüge der Bevölkerungsgeographie. Lehrbehelf zur Lehrveranstaltung, Universität Wien, Institut für Geographie und Regionalforschung, S. 42.