Weibull-Verteilung

Die Weibull-Verteilung ist eine statistische Verteilung, die beispielsweise zur Untersuchung von Lebensdauern in der Qualitätssicherung verwendet wird. Man verwendet sie vor allem bei Fragestellungen wie Materialermüdungen von spröden Werkstoffen oder Ausfällen von elektronischen Bauteilen, ebenso bei statistischen Untersuchungen von Windgeschwindigkeiten. Benannt ist sie nach dem Schweden Waloddi Weibull (1887-1979).

Ein anschauliches Beispiel für die Anwendung der Weibull-Statistik ist die Ausfallwahrscheinlichkeit einer Kette. Das Versagen eines Glieds führt zum Festigkeitsverlust der ganzen Kette. Spröde Werkstoffe zeigen ein ähnliches Bruchverhalten. Es genügt ein Riss, der die kritische Risslänge überschreitet, um das Bauteil zu zerstören.

So erklärt sich auch die Abhängigkeit der Festigkeit spröder Werkstoffe von der Geometrie. Das Verlängern einer Kette (bzw. eines spröden Bauteils) reduziert die Festigkeit, eine Verstärkung der Kettenglieder erhöht sie.

Die Weibull-Verteilung kann zur Beschreibung steigender, konstanter und fallender Ausfallraten technischer Systeme verwendet werden.

In der Praxis ist die Weibull-Verteilung neben der Exponentialverteilung die am häufigsten verwendete Lebensdauerverteilung.

Definition

Dichten der Weibullverteilung

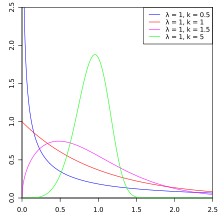
Die Dichtefunktion der Weibull-Verteilung $\operatorname{Wei}(\alpha,\beta)$ ist

$f(x)=\lambda \cdot k \cdot ( \lambda \cdot x )^{k - 1} \mathrm{e}^{- ( \lambda \cdot x)^ k}$

und ihre Verteilungsfunktion lautet

$F(x)=1-\mathrm{e}^{- \lambda \cdot x^ k}$

für x > 0, λ > 0 und k > 0.

Die Grafik zeigt die Dichtefunktionen der Weibull-Verteilung für verschiedene Werte von k.

Spezialfälle der Weibull-Verteilung

Einige Verteilungen lassen sich als Spezialfall der Weibull-Verteilung beschreiben:

• Für k = 1 ergibt sich die Exponentialverteilung mit einer streng monoton fallenden Ausfallrate.
• Für k = 2 ergibt sich die Rayleigh-Verteilung
• Für k = 3,4 ergibt sich eine Verteilung ähnlich der Normalverteilung

Bei Systemen mit unterschiedlichen Ausfallursachen lassen sich diese mit drei Weibull-Verteilungen so abbilden, dass sich die bekannte Badewannen-Kurve darstellen lässt.^[1]. Die Verteilungen decken dann diese drei Bereiche^[2] ab:

• Frühausfälle mit β < 1, beispielsweise in der Einlaufphase
• Zufällige Ausfälle mit β = 1 in der Betriebsphase
• Ermüdungs- und Verschleißausfälle am Ende der Produktlebensdauer mit β > 1

Verbreitete Darstellung

Weibullnetz

Die Verteilungsdichte lautet hierbei

$f(t)=\frac{b}{T} \cdot \left(\frac{t}{T}\right)^{b-1} \cdot \mathrm{e}^{-\left(\displaystyle\frac{t}{T}\right)^{\displaystyle b}}$

mit der Verteilungsfunktion

$F(t)=1-\mathrm{e}^{-\left(\displaystyle\frac{ t}{T}\right)^{\displaystyle b}}$

für t > 0, T > 0 und b > 0. Dabei ist t die Zeit (oder Festigkeit, ...), T die charakteristische Lebensdauer (d.h. Lebensdauer bei einer Ausfallwahrscheinlichkeit von 63,2 %, Festigkeitsniveau bei einer Ausfallwahrscheinlichkeit von 63,2 %, ...). Der Weibull-Modul b beschreibt die Streuung von Defekten in einer Probe. Je größer b, desto geringer die Streuung und damit auch die Streuung der Festigkeiten.

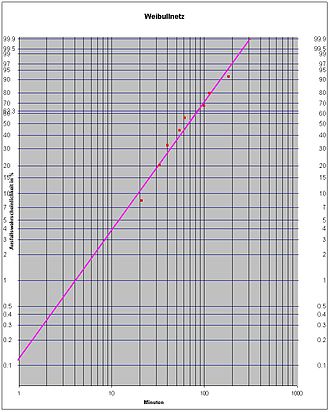
Trägt man die Verteilung in der Form

$\ln{(\ln{\frac{1}{1-F(t)})}}=b \cdot \ln(t) - b \cdot \ln(T)$

auf, ergibt sich eine Gerade, bei der man den Parameter b leicht als Steigung ablesen kann. Der Parameter T kann dann folgendermaßen berechnet werden:

$T=\mathrm{e}^{-\left(\displaystyle\frac{a}{b}\right)}$

Hierbei bezeichnet a den y-Achsenabschnitt.

Oft kommt es vor, dass trotz Beanspruchung erst nach einer Betriebszeit t₀ Ausfälle überhaupt eintreten (Bremsbelag verschlissen, ...). Auch dies kann in der Weibull-Verteilungsfunktion berücksichtigt werden. Sie hat dann folgendes Aussehen:

$F(t)=1-\mathrm{e}^{-\left(\displaystyle\frac{t-t_0}{T-t_0}\right)^{\displaystyle b}}$

Trägt man die Funktion wieder auf, ergibt sich keine Gerade, sondern eine nach oben konvexe Kurve. Verschiebt man alle Punkte um den Wert t₀, so geht die Kurve in eine Gerade über.

Eigenschaften

Erwartungswert

Den Erwartungswert erhält man zu

$\operatorname{E}(X)=\alpha^{-1/ \beta} \cdot \Gamma\left(\frac{1}{\beta}+1\right)$.

Varianz

Die Varianz bestimmt sich zu

$\operatorname{Var}(X)=\alpha^{-2/ \beta} \cdot \left(\Gamma\left(\frac{2}{\beta}+1\right)- \Gamma \left(\frac{1}{\beta}+1\right)^2\right)$,

wobei Γ die Gammafunktion bezeichnet.

Schiefe

Die Schiefe ergibt sich zu

$\operatorname{v}(X)=\frac{\left(\frac{1}{\beta}+1\right)\left[\frac{2}{\beta}+1-\Gamma\left(\frac{1}{\beta}+1\right)\right]} {\left(\frac{1}{\beta}+1-\Gamma\left(\frac{1}{\beta}+1\right)\right)^{\frac{3}{2}}\Gamma^{\frac{1}{2}}\left(\frac{1}{\beta}+1\right)}-2\frac{\Gamma^{\frac{1}{2}}\left(\frac{1}{\beta}+1\right)} {\left(\frac{1}{\beta}+1-\Gamma\left(\frac{1}{\alpha}+1\right)\right)^{\frac{1}{2}}}$

Beziehung zu anderen Verteilungen

Beziehung zur Exponentialverteilung

• Man sieht, dass der Fall β = 1 die Exponentialverteilung $\operatorname{Exp}(\alpha)$ ergibt. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate α. Untersucht man jedoch Fragestellungen mit steigender (β > 1) oder fallender (β < 1) Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über.
• Ist der Parameter β > 1, dann wird ein System mit einer mit der Zeit ansteigenden Ausfallrate, also ein alterndes System, beschrieben.
• Besitzt X eine Exponentialverteilung $\operatorname{Exp}(\alpha)$ mit Parameter α, dann besitzt die Zufallsvariable $Y := X^c ~(c>0)$ eine Weibull-Verteilung $\operatorname{Wei}(\alpha, 1/c)$. Zum Beweis betrachte man die Verteilungsfunktion von Y:
  $F_Y(y) = P(Y \le y) = P(X^c \le y) = P(X \le y^{1/c}) = 1 - e^{-\alpha \cdot y^{1/c}},~y > 0$.
  Das ist die Verteilungsfunktion einer Weibull-Verteilung.

Gestreckte Exponentialfunktion

Die Funktion

$1-F(x)=\mathrm{e}^{- \alpha x^ \beta}$

ist als gestreckte Exponentialfunktion bekannt.

Siehe auch

• Mortalität
• Extremwerttheorie

Literatur

• Bernard W. Lindgren: Statistical Theory. Chapman & Hall, New York u. a. 1993, ISBN 0-412-04181-2.
• Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. Deutscher Verlag der Wissenschaften, Berlin 1970.
• Joachim Hartung, Bärbel Elpelt, Karl-Heinz Klösener: Statistik. Oldenbourg, München 2002, ISBN 3-486-25905-9.
• Horst Rinne, Hans-Joachim Mittag: Statistische Methoden der Qualitätssicherung. Hanser, München/Wien 2002, ISBN 3-446-15503-1.
• Holger Wilker: Weibull-Statistik in der Praxis, Leitfaden zur Zuverlässigkeitsermittlung technischer Produkte. BoD, Norderstedt 2004.

Weblinks

 Commons: Weibull-Verteilung – Sammlung von Bildern, Videos und Audiodateien

• Weibull-Verteilung in der Zuverlässigkeitsanalyse
• Weibull-Verteilung und deren Anwendung bei Keramiken
• Praktikumsanleitung zur Bestimmung der Weibull-Verteilung bei Keramiken

Quellen

1. ↑ Siehe auch:en:Exponentiated Weibull distribution
2. ↑ Zuverlässigkeitssicherung bei Automobilherstellern und Lieferanten. 3. Auflage. VDA, Frankfurt a. M. 2000, ISSN 0943-9412, Abschnitt 2.4.3. (Qualitätsmanagement in der Automobilindustrie 3)

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta