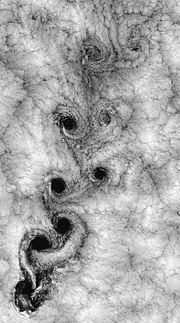
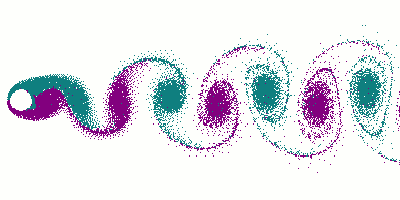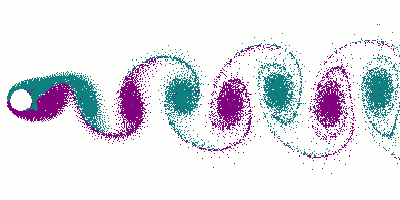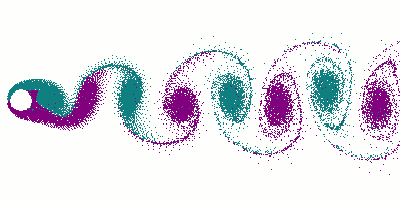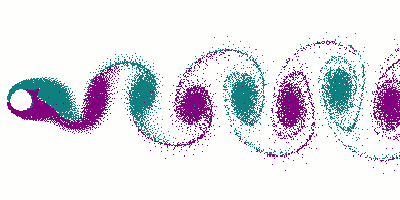Karmansche Wirbelstraße

Animation zur Ausbildung einer Wirbelstraße

Als Kármánsche Wirbelstraße bezeichnet man ein Phänomen in der Strömungsmechanik, bei der sich hinter einem umströmten Körper gegenläufige Wirbel ausbilden. Die Wirbelstraßen wurden von Theodore von Kármán erstmals 1911 nachgewiesen und berechnet.

Wirbelbildung

Wird ein Körper mit niedriger Geschwindigkeit angeströmt, fließt die Strömung bei einer kleinen Reynolds-Zahl Re laminar - beispielsweise für eine Rohrströmung bis Re < Re_krit ≈ 2300. Bei zunehmender Geschwindigkeit (höherer Reynoldszahl) bilden sich zunächst stationäre Wirbel aus. Bei weiterer Zunahme der Strömungsgeschwindigkeit lösen sich die Wirbel ab und bilden ein mehr oder weniger periodisch verlaufendes Wirbelsystem aus. Die Frequenz der Wirbelablösungen wird durch die Strouhal-Zahl charakterisiert. Die "Schleppe" aus sich am umströmten Körper bildenden, von der Strömung fortgetriebenen und schließlich dissipierten Wirbeln bildet die sog. Kármánsche Wirbelstraße. Die Wirbel entstehen an der linken und rechten Seite des umströmten Körpers. Ihr Drehsinn ist entgegengesetzt zueinander. Die Strömung zwischen ihnen verläuft in Richtung zum umströmten Körper, also gegenläufig zur äußeren Strömung. Dieses Muster ist noch stabil bis zu Reynoldszahlen von rund 10.000. Danach wird das Strömungsfeld turbulent. Außerhalb der turbulenten Zone kann die Strömung laminar abfließen. Dadurch verringert die Zone den Strömungswiderstand des Körpers.

Beispiele

Satellitenaufnahme der Juan-Fernández-Inseln

Mit Pfeilen markiert sind die Wasserwirbel in einem kleinen Bach. Bei einem kleineren Stein würden sich die Wirbel auf beiden Seiten vereinigen.

Wirbel und Wirbelstraßen sind ein häufiges Phänomen. Ihre Beobachtung ist jedoch nicht ganz einfach. Luftströmungen lassen sich nicht ohne weiteres erkennen. Wasserwirbel sind genauso durchscheinend wie Wasser selbst. Bei genauer Beobachtung wird man sie in der Badewanne entdecken, wenn man mit dem Finger durch das Wasser fährt. Versetzt man eine Flüssigkeit hoher Viskosität, z. B. ein Wasser-Glyzeringemisch, teilweise mit Lebensmittelfarbe, lassen die Farbfäden die Rotationsrichtungen erkennen.

Die

Kármánsche Wirbelstraßen können sich beispielsweise hinter Inselgruppen bilden, die hoch aus dem Meer ragen. Die Turbulenzen sind dann auf Luftaufnahmen als riesige Wolkenstrukturen erkennbar, siehe die Satellitenaufnahme rechts.

Ablösefrequenz

Die Ablösefrequenz f der Wirbel kann über die Strouhalzahl Sr bestimmt werden. Es gilt:

$f = Sr \cdot \frac{v}{d}$ ,

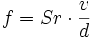wobei v für die Anströmgeschwindigkeit und d für eine charakteristische Abmessung des umströmten Körpers steht. Die Strouhalzahl Sr ist von der Form des Körpers abhängig. Für zylindrische Körper beträgt sie 0,2; als charakteristische Abmessung wird hier der Durchmesser eingesetzt. Somit erzeugt z. B. eine 4 mm dicke Radioantenne auf dem Dach eines 90 km/h (25 m/s) schnell fahrenden Fahrzeugs einen oft deutlich hörbaren Ton mit der Frequenz

$f = 0{,}2 \cdot \frac{25}{0{,}004}\ \mathrm{Hz} = 1250\ \mathrm{Hz}$.

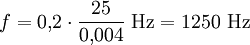Ein weiteres Beispiel ist das Pfeifen singender Stromdrähte im Wind.

Aufgrund des linearen Zusammenhangs von Ablösefrequenz und Strömungsgeschwindigkeit wird der physikalische Effekt für die Durchfluss-Messung („Vortex-Durchflussmesser“) bei nicht-abrasiven (siehe: Verschleiß), niederviskosen Medien genutzt.

Resonanzfall

Entspricht die Ablösefrequenz der Wirbel der Eigenfrequenz des umströmten Körpers, wird er in Schwingung versetzt. Ein bekanntes Beispiel sind Aeolsharfen.

Im Extremfall zerstören die Schwingungen Bauwerke. So stürzte am 7. November 1940 die Tacoma Narrows Bridge, eine 850 m lange Hängebrücke im Bundesstaat Washington ein. Ein leichter Sturm mit einer Windgeschwindigkeit von ca. 70 km/h führte zur Ausbildung einer Kármánschen Wirbelstraße, deren Wirbel sich an den Rändern der Brücke mit einer Frequenz ablösten, die der Eigenfrequenz der Brücke entsprachen. Durch die auftretende Resonanzschwingung schaukelte sich die Brücke immer weiter auf, bis sie nach ca. einer Stunde auseinander brach.

Siehe auch

• Aeroakustik