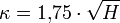Kimmlinie

Horizontlinie (Computergrafik)

Der Horizont (griech. ορίζοντας „der Gesichtskreis“) ist die Grenzlinie zwischen der sichtbaren Erde und dem Himmel. Der Begriff Horizont wurde von Philipp von Zesen durch den Ausdruck Gesichtskreis eingedeutscht. Die vom Horizont aufgespannte Ebene ist die Horizontebene oder Horizontalebene; sie steht rechtwinklig zur Zenit- oder Lotrichtung.

Präzise Definitionen

Genauer betrachtet sind einige Bedeutungen zu unterscheiden, die sich alle durch unterschiedliche Sichtweiten und scheinbare Entfernungen zum Horizont unterscheiden:

• Geometrischer Horizont: Er ist die Schnittlinie der Himmelskugel mit einer Ebene, die im Beobachtungsort senkrecht zur – um die Lotabweichung korrigierte – Lotrichtung ist (Transversalebene) – das ist im allgemeinen nicht die Richtung vom Standpunkt des Beobachters zum Erdmittelpunkt, die gilt nur bei einem exakt kugelförmigen Erdmodell
• Optischer Horizont: Durch die Lichtbrechung erscheint der Horizont weiter entfernt und die Erde größer.
• Radiohorizont: Radiowellen verhalten sich ähnlich wie Licht. Auch hier wird die Brechung durch einen größeren scheinbaren Erddurchmesser berücksichtigt.
• Nautischer Horizont, Kimmung, Kimmlinie: der natürliche Horizont am Meer.
• Natürlicher oder Landschaftshorizont: die Grenzlinie zwischen Himmel und Erde, wie sie von den örtlichen Bedingungen (der Landschaft) abhängt.

Horizontebene ist die Ebene des geometrischen Horizonts. Die Vertikale auf diese Ebene schneidet die Himmelssphäre in Zenit und Nadir.

Horizont in der Nautik, Kimmlinie

Die Kimm ist die auf offenem Meer sichtbare Grenzlinie zwischen Wasser und Himmel. Auf sie beziehen sich Messungen von Höhenwinkeln z. B. mit einem Sextanten.

Wegen der Erdkrümmung (mittlerer Erdradius 6371 km) erscheint die Kimm umso tiefer unter dem mathematischen Horizont, je höher sich der Beobachter über dem Meeresspiegel befindet.

Daher müssen die Höhenwinkel um die Kimmtiefe verkleinert werden. Diese Beschickung beträgt

$\kappa=1{,}75\cdot\sqrt{H}$

(in Bogenminuten; Höhe H in Metern; Details siehe Artikel Sichtweite.)

Nach der DIN 13312 "Navigation; Begriffe, Abkürzungen, ..." soll für die Kimmtiefe in der Seefahrt die Abkürzung Kt, im Englischen die Abkürzung D (von "dip of horizon"), in der Luftfahrt die Abkürzung Dip verwendet werden; als Formelzeichen wird für die Seefahrt k empfohlen.

Horizont in Mathematik, Astronomie und Geodäsie

Blick auf den Erdhorizont (Space Shuttle Endeavour, 2002)

Der Horizont im mathematischen Sinn ist ein Großkreis, der die Sphäre oder Himmelskugel in zwei gleiche Hälften teilt und dessen Pol der Zenit ist.

Geometrischer Horizont

ein Großkreis im o.e. Sinn, der in der Astronomie zwei Bezugspunkte kennt:

• Geozentrischer (Wahrer) Horizont: die horizontale Ebene geht durch den Erdmittelpunkt
• Topozentrischer (Scheinbarer) Horizont (häufiger verwendet): durch einen Ort an der Erdoberfläche, beziehungsweise durch den Standpunkt des Beobachters. Der Unterschied im Höhenwinkel eines Gestirns entspricht der Parallaxe, während die Azimute dieselben sind.

Er ist die Basis des Horizontsystems - ein Koordinatensystem, in dem Gestirne und terrestrische Messpunkte durch Richtung (Azimut, Kurs) und Höhenwinkel angegeben werden. Senkrecht zum Horizont - also durch den Zenit - verlaufen die Vertikalkreise, von denen der Meridian genau in Nord-Süd-Richtung liegt.

Siehe auch

• Dämmerung, Sonnenaufgang, Sonnenuntergang
• Künstlicher Horizont – Messinstrument zur Ermittlung der Horizontalen