Kreisteilungsgleichung

Das Problem der Kreisteilung ist eine schon in der Antike untersuchte Konstruktionsaufgabe der Geometrie. Es geht darum, für eine gegebene natürliche Zahl n einen Kreis unter ausschließlicher Verwendung von Zirkel und Lineal in n gleich große Kreisbögen zu zerlegen. Diese Aufgabe ist gleichwertig zur Konstruktion eines regelmäßigen Polygons (Vielecks) mit n Ecken.

Das Problem ist in einigen Fällen einfach zu lösen, etwa für n=3 (gleichseitiges Dreieck), n=4 (Quadrat) oder n=6 (regelmäßiges Sechseck). Die Kreisteilung für n=5, also die Konstruktion eines regelmäßigen Fünfecks bzw. eines 72°-Winkels ist eng verknüpft mit dem Begriff des Goldenen Schnittes. Allerdings ist die Kreisteilung mit Zirkel und Lineal in vielen Fällen unmöglich, beispielsweise schon für n=7 oder n=9. Als es 1796 dem Mathematiker Carl Friedrich Gauß unter Anwendung algebraischer Methoden gelang, ein regelmäßiges 17-Eck zu konstruieren, war dies für seine Zeitgenossen eine Sensation.

Algebraisch betrachtet, lässt sich die Konstruktion des regelmäßigen n-Ecks zurückführen auf die Kreisteilungsgleichung

$z^n \, = \, 1$.

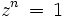Die Variable z in dieser Gleichung ist eine komplexe Zahl. Das geometrische Kreisteilungsproblem ist genau dann lösbar, wenn die Kreisteilungsgleichung eine Lösung hat, die sich durch rationale Zahlen, die vier Grundrechenarten, Klammern, Quadratwurzeln sowie die imaginäre Einheit i ausdrücken lässt. In welchen Fällen dieses Kriterium erfüllt ist, lässt sich mit der Galoistheorie untersuchen. Eine entscheidende Rolle dabei spielen die Kreisteilungspolynome. Ergebnis dieser Überlegungen ist der folgende Satz:

Ein regelmäßiges Vieleck mit n Ecken lässt sich genau dann mit Zirkel und Lineal konstruieren, wenn sich n in der Form

$n \, = \, 2^k \cdot p_1 \cdot \ldots \cdot p_m$

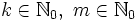mit $k\in\mathbb{N}_0, \; m\in\mathbb{N}_0$ schreiben lässt, wobei die Faktoren $p_1,\;\ldots,\;p_m$ paarweise verschiedene fermatsche Primzahlen, also Primzahlen der Form 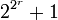$2^{2^r}+1$ sind.