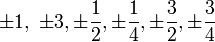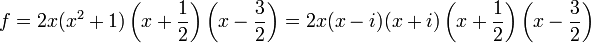- Lemma von Gauß
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Als Inhalt (engl. content) eines Polynoms bezeichnet man die Zahl, durch die man ein Polynom aus dem Quotientenkörper eines Ringes dividieren muss, sodass der größte gemeinsame Teiler seiner Koeffizienten eine Einheit im Ring ist. Die Abhängigkeit vom Ring ist dabei essenziell.
Seine Anwendung hat dieser Begriff im Satz von Gauß. Dieser stellt den Inhalt eines Produktes von zwei Polynomen in Bezug zum Inhalt seiner Faktoren. Dieses Resultat ist theoretisch sehr interessant, da man damit nachweisen kann, dass Polynomringe in endlich vielen Variablen über faktoriellen Ringen insbesondere über Körpern faktoriell sind. Praktisch kann man den Satz auch nutzen um Einschränkungen von rationalen Nullstellen eines Polynoms mit ganzen Koeffizienten zu erhalten (Insbesondere lassen sich die Kandidaten für rationale Nullstellen auf endlich viele reduzieren). Dies kann bei der Faktorisierung von Polynomen nützlich sein.
Inhaltsverzeichnis
Definition (für einen faktoriellen Ring)
Sei
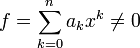 ein Polynom mit Koeffizienten aus einem beliebigen faktoriellen Ring R. Dann ist
ein Polynom mit Koeffizienten aus einem beliebigen faktoriellen Ring R. Dann ist 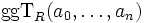 der Inhalt von f und wird im Folgenden mit inhaltR(f) bezeichnet, wobei in der Literatur teilweise auch die englische Bezeichnung contR(f) verwendet wird. Der Inhalt ist bis auf eine Einheit eindeutig bestimmt. Weiter ist festgelegt.
der Inhalt von f und wird im Folgenden mit inhaltR(f) bezeichnet, wobei in der Literatur teilweise auch die englische Bezeichnung contR(f) verwendet wird. Der Inhalt ist bis auf eine Einheit eindeutig bestimmt. Weiter ist festgelegt.- inhaltR(0): = 0
Weiter ergibt sich mit dieser Definition eine sinnlose Beschränkung im Lemma von Gauß auf Polynome aus dem Ring.
Definition (für den Quotientenkörper über einem faktoriellen Ring)
Es sei R ein faktorieller Ring und K der Quotientenkörper. Die Elemente des Quotientenkörpers kann man mit Hilfe der Primelemente wie folgt schreiben.
Die auftretenden Exponenten sind eindeutig bestimmt und man kann definieren
Damit lässt sich nun die Ordnung für ein Polynom mit Koeffizienten aus dem Körper K bestimmen.
Weiter lässt sich nun der Inhalt definieren über
Dabei sei P eine maximale Menge paarweise nicht assoziierter Primelemente aus R und
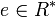 eine beliebige Einheit. Zur Vollständigkeit gilt noch
eine beliebige Einheit. Zur Vollständigkeit gilt nochWie im Falle eines Quotientenkörpers ist der Inhalt bis auf Assoziiertheit eindeutig bestimmt. Es ist klar, dass die beiden Definitionen für Polynome über dem Ring gleich sind.
Beispiel
Beispiel 1 (Zur 1. Definition):
Der Inhalt von f = 6x3 + 9x + 12 als Polynom mit Koeffizienten aus
 ist
istoder auch − 3. Fassen wir f dagegen als Polynom mit Koeffizienten aus
 auf, so erhalten wir
auf, so erhalten wiroder jede andere rationale Zahl außer der Null.
Beispiel 2 (Zur 2. Definition):Der Inhalt von
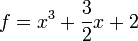 als Polynom mit Koeffizienten aus
als Polynom mit Koeffizienten aus 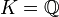 als Quotientenkörper von
als Quotientenkörper von 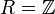 ist
istoder auch − 0,5. Fassen wir f benutzt man dagegen
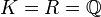 , so erhalten wir
, so erhalten wiroder jede andere rationale Zahl außer der Null.
Unterschiede machen die beiden Definitionen für Polynome mit Koeffizienten aus R nicht, wie man aber auch an den Definitionen erkennt.Falls klar ist, aus welchem Ring die Koeffizienten von f stammen, schreiben wir einfach inhalt(f).
Bemerkungen
Polynome, deren Inhalt eine Einheit ist heißen primitiv. Mit
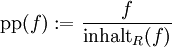 wird der primitive Anteil (engl. primitive part) bezeichnet.
wird der primitive Anteil (engl. primitive part) bezeichnet.Ein Polynom mit Koeffizienten aus dem Quotientenkörper von einem faktoriellen Ring ist genau dann aus dem Polynomring über dem faktoriellen Ring, wenn der Inhalt im Ring selbst liegt.
Lemma von Gauß
Inhalt
Es sei R ein faktorieller Ring und K sein Quotientenkörper, dann gilt für
![f,g\in K[X]](/pictures/dewiki/97/a4399c4d7400b86cb17fa08c9e1b3ca3.png)
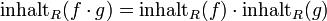 ,
,
insbesondere ist das Produkt zweier primitiver Polynome wieder primitiv.
Korollare
Als „Lemma von Gauß“ werden oft auch die vier folgenden Korollare aus dieser Aussage bezeichnet:
- Der Polynomring R[X] über einem faktoriellen Ring R ist faktoriell.
- Wenn ein nicht-konstantes Polynom (in einer Variablen) über einem faktoriellen Ring irreduzibel ist, dann ist es auch über seinem Quotientenkörper irreduzibel.
- Wenn ein normiertes Polynom eine Nullstelle im Quotientenkörper hat, dann liegt diese bereits im Ring selbst.
- Das Produkt zweier normierter Polynome f,g mit rationalen Koeffizienten hat nur dann ganzzahlige Koeffizienten, wenn bereits die Koeffizienten von f und g ganzzahlig sind.
Weitere Korollare sind:
- Ist ein Polynom aus dem Ring gegeben, so kann jede Nullstelle im Quotientenkörper der Art als Bruch dargestellt werden, dass der Nenner ein Teiler des höchsten Koeffizienten und der Zähler ein Teiler des absolut Gliedes ist.
- Die Primelemente in dem Polynomring R[X] über einem faktoriellen Ring R sind genau die Primelemente des Ringes zusammen mit den primitiven Primelementen des Polynomringes K[X] über dem Quotientenkörper K von R.
- Ist R ein faktorieller Ring, dann ist der Polynomring in endlich vielen Variablen R[X1,...,Xn] faktoriell.
- Ist K ein Körper, dann ist der Polynomring in endlich vielen Variablen K[X1,...,Xn] faktoriell, aber für n > 1 kein Hauptidealring, aber noch noethersch.
Beweisidee
Zuerst überzeugt man sich, dass dies für
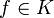 gilt. Man kann also annehmen, dass f,g primitiv (also
gilt. Man kann also annehmen, dass f,g primitiv (also ![f,g,fg\in R[X]](/pictures/dewiki/50/269be7aa73b415998c8149865646cf6e.png) ) sind und muss somit nur diesen Spezialfall des Satzes zeigen . Man erkennt auch leicht, dass
) sind und muss somit nur diesen Spezialfall des Satzes zeigen . Man erkennt auch leicht, dassDann ist der Satz aber trivial, denn R / pR und damit (R / pR)[X] ist ein Integritätsbereich, weil pR ein Primideal ist.
Zum ersten Korollar:
Man beweist, dass alle Primelemente des Ringes und alle primitiven Primelemente von K[X] prim in R[X] sind. Wenn man den Fakt ausnutzt, dass K[X] als Euklidischer Ring faktoriell ist, kann man jedes Element aus R[X] als Produkt dieser Primelemente schreiben (dies musste man zeigen). Die anderen Korollare benötigen keine Beweisidee. Man muss einfach die Aussagen direkt nachweisen.
Historisch
Gauß selbst zeigt in den Disquisitiones Arithmeticae (art. 42) die Variante:
- Das Produkt zweier normierter Polynome f,g mit rationalen Koeffizienten hat nur dann ganzzahlige Koeffizienten, wenn bereits die Koeffizienten von f und g ganzzahlig sind.
Anwendung
- f = 6x7 + 23x3 + 9x2 − 12x + 24 ist nicht durch g = 6x4 + 9x3 + 3x2 + 3x + 3 teilbar in
![\mathbb Z[X]](/pictures/dewiki/101/ef616d0b1baef82f69bc42b50836f19a.png) , denn der Inhalt von f ist 1 und von g 3.
, denn der Inhalt von f ist 1 und von g 3. - f = 2x7 + x3 + x2 + 3x + 1 hat keine rationalen Nullstellen, denn die einzig möglichen rationalen Nullstellen wären nach Gauß
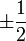 und
und 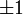 .
. - f = 2x3 + 2x + 3 ist irreduzibel als Polynom in
 , denn es hat Grad 3 und keine rationale Nullstellen (Mit Gauß muss man nur endlich viele überprüfen).
, denn es hat Grad 3 und keine rationale Nullstellen (Mit Gauß muss man nur endlich viele überprüfen). - f = 8x5 − 8x4 + 2x3 − 8x2 − 6x ist als Polynom in
 zu faktorisieren. Dabei nimmt man zuerst folgende triviale Faktorisierungen vor (primitiv machen und x mit maximaler Potenz ausklammern!):
zu faktorisieren. Dabei nimmt man zuerst folgende triviale Faktorisierungen vor (primitiv machen und x mit maximaler Potenz ausklammern!):
-
- f = 8x5 − 8x4 + 2x3 − 8x2 − 6x = 2x(4x4 − 4x3 + x2 − 4x − 3)
- Und damit hat das verbleibende Polynom die möglichen rationalen Nullstellen nach Gauß
- Durch Einsetzen erkennt man, dass nur − 0,5 und 1,5 die rationalen Nullstellen sind. Und durch Polynomdivision ergibt sich
Literatur
- Serge Lang: Algebra. Springer-Verlag.
- Van der Waerdens: Moderne Algebra. Springer-Verlag (aus Vorlesungen von Emil Artin und Emmy Noether).
- Siegfried Bosch: Algebra. Springer.
- Michael Artin: Algebra. Birkhäuser-Verlag.
- Atilla Pethö; Michael Pohst (Hrsg.): Algebraische Algorithmen. Vieweg, 1999, ISBN 9783528065980.
- Michael Kaplan: Computeralgebra. Springer-Verlag, 2005, ISBN 3540213791.
Wikimedia Foundation.

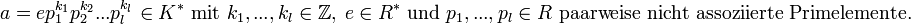
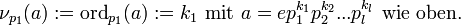
![\mathrm{ord}_p(f):=\nu_p(f):=\min\limits _{i=0,...,n}\nu_p(a_i)\text{, wobei }f = \sum_{k=0}^n a_k x^k\in K[X]\backslash\{0\}](/pictures/dewiki/52/43a7d9fe546bd85bdf48529d93d5829e.png)
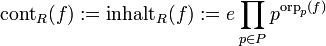
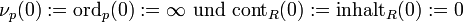
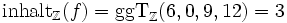
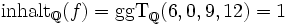
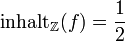
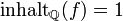
![\mathrm{inhalt_R}(f)=1\Leftrightarrow\forall p\text{ Primelement}:\ f+pR[X]\neq 0\in R[X]/pR[X]\cong (R/pR)[X]](/pictures/dewiki/101/e3f462bcf091d210dd82deb55a2f289e.png)