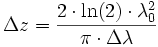Optische Koheränztomographie

Optische Kohärenztomografie (engl. optical coherence tomography, OCT) ist ein Untersuchungsverfahren, bei dem Licht geringer Kohärenzlänge mit Hilfe eines Interferometers zur Entfernungsmessung reflektiver Materialien eingesetzt wird. Vorteile gegenüber konkurrierenden Verfahren sind die relativ hohe Eindringtiefe (1–3 mm) in streuendes Gewebe und gleichzeitige hohe axiale Auflösung (0,5–15 µm) bei hoher Messgeschwindigkeit (20–300 kvoxel/s). Das entsprechende akustische Verfahren ist die Ultraschalldiagnostik (Sonografie). Es unterscheidet sich von den winkelabhängigen 3D-Messverfahren (wie sie auch das menschliche Auge verwendet) durch seine rein axiale Tiefenbestimmung unter Ausnutzung eines Spektralbereiches (statt eines Winkelbereichs) und der damit einhergehenden Unabhängigkeit von der numerischen Apertur des Instruments.

Optische Kohärenztomographie der Fingerkuppe (Leistenhaut) mit Schweißdrüsengängen, Seitenlänge 1 × 1 mm², Tiefe ca. 600 µm

Prinzip

Weißlichtinterferometrie und TD-OCT

Das Grundprinzip der OCT basiert auf der Weißlichtinterferometrie, dieses Verfahren vergleicht die Laufzeit eines Signals mit Hilfe eines Interferometers (meist Michelson-Interferometer). Dabei wird der eine Arm mit bekannter optischer Weglänge (= Referenzarm des Interferometers) als Referenz zum Messarm herangezogen.

Die Interferenz der Signale (optische Kreuzkorrelation) aus beiden Armen ergibt ein Muster, aus dem man die relative optische Weglänge innerhalb eines Tiefenprofils (amplitude-mode scan) herauslesen kann. In den eindimensionalen Rasterverfahren wird der Strahl dann transversal in einer oder zwei Richtungen geführt, womit sich ein flächiges Tomogram (Brightness-mode scan oder ein dreidimensionales Volumen (c-mode scan) aufnehmen lässt.

transversale und axiale Auflösung in der OCT

Die herausragende Eigenschaft der OCT ist die Entkoppelung der transversalen von der longitudinalen Auflösung. In der konventionellen Lichtmikroskopie hängt sowohl die axiale Auflösung (in der Tiefe) als auch die transversale (seitliche) Auflösung von der Fokussierung des Lichtstrahles ab. Der Parameter für die Fokussierbarkeit ist die Numerische Apertur. Bei der OCT ist die Auflösung nur durch die Bandbreite des verwendeten Lichtes begrenzt, das heißt, hohe Auflösung – kleine Details können aufgelöst werden – wird mit großen Bandbreiten (weiten Spektren) erreicht.

Anwendung

Anwendungsbereiche liegen primär in der Medizin, dort vor allem in der Augenheilkunde, sowie zur frühzeitigen Krebsdiagnose und zur Hautuntersuchung. Hier werden Reflexionen an Grenzflächen (siehe auch Fresnelsche Formeln) von Materialien mit unterschiedlichen Brechzahlen (z. B. zwischen Membranen, Zellschichten, Organgrenzen etc. …) ausgemessen und so ein dreidimensionales Bild rekonstruiert. Eine solche Rekonstruktion wird als Tomografie bezeichnet.

In vivo OCT Scan einer Retina bei 800 nm und einer axialen Auflösung von 3 µm

Der Haupteinsatz liegt derzeit bei der Untersuchung des Augenhintergrundes, bzw. des hinteren Augenabschnittes, da konkurrierende Techniken wie z. B. das Konfokalmikroskop die feine Schichtstruktur der ca. 250–300 µm dicken Netzhaut aufgrund der geringen Pupillengröße und des großen Abstandes von Hornhaut zur Netzhaut nur unzureichend abbilden können. Andere Verfahren wiederum eignen sich nicht aufgrund ihrer hohen Belastung des menschlichen Auges, bzw. werden vom Glaskörper des Auges zu stark beeinträchtigt (z. B. hochauflösendes Ultraschall). Gerade hier ist das berührungslose Messen ein unschätzbarer Vorteil, da damit Infektionsrisiken und die psychische Belastung weitgehend vermieden werden.

Ein neues Einsatzgebiet des OCT ist die kardiovaskuläre Bildgebung. Die intravaskuläre optische Kohärenztomografie (OCT) ist eine neue, auf Infrarotlicht basierende Technik, die Arterien mit einer Auflösung von 10–20 µm darstellen kann. Verschiedene präklinische sowie klinische Serien zeigten, das OCT eine sichere Identifikation intramuraler sowie luminaler Morphologien ermöglicht, z. B. Plaques, Thromben, Dissektionen sowie Informationen über Lumen und Stentdimensionen. Studien zum Vergleich von IVUS und OCT zeigten, dass OCT zusätzliche morphologische Informationen erbringt, welche eine verbesserte Plaquecharakterisierung erlauben.

Axiale Auflösung und Bandbreite

Nach anfänglichen Versuchen mit Lichtquellen beschränkter Bandbreite (einige Nanometer) wurden relativ breitbandige Lichtquellen mit hoher räumlicher Kohärenz verfügbar und eingesetzt. Zumeist basierten die Systeme auf Superlumineszenzdioden mit einigen zehn Nanometer Bandbreite (typ. 30 nm, entspricht mehr als 30 µm Auflösung.). Erst im Jahre 1997 wurde erfolgreich der Sprung von dieser Standardauflösung bis zur „Ultrahochauflösung“ gewagt (>100 nm, entspricht weniger als 3 µm axialer Auflösung), die Tomogramme vergleichbar mit histologischen Schnitten ermöglicht.

Axiale Auflösung in der OCT bei variierender Bandbreite und zentraler Wellenlänge für unterschiedliche Lichtquellen

Folgende Formel (hergeleitet aus dem Fourierverhältnis zwischen Korrelationsbreite und spektraler Breite, gemessen bei voller Breite auf halber Höhe) erlaubt es bei einem Spektrum mit Gauß-Verteilung die zugehörige axiale Auflösung zu berechnen:

${\Delta z} = {{2 \cdot \ln(2) \cdot \lambda_0^2} \over {\pi \cdot \Delta \lambda}}$

Δz = axiale Auflösung

λ₀ = zentrale Wellenlänge

Δλ = volle spektrale Bandbreite bei halber Höhe des Spektrums (FWHM) Annahme: gaußförmiges Spektrum

Die Dispersion im menschlichen Gewebe, und vor allem im Glaskörper des Auges zerstört die Kohärenz der beiden Arme. Geschicktes Ausbalancieren der Dispersion in beiden Armen ermöglicht aber ein Restituieren der Kohärenz. Die Präzision der ultrahochauflösenden OCT haben zu einem Umdenken in der Augenheilkunde geführt, da Augenärzte plötzlich Informationen erhalten können, die sie nur aus dem Lehrbuch kannten. Dies ermöglicht bereits kleinste Veränderungen in Frühstadien zu erkennen, was mit anderen Methoden nur schwer oder gar nicht möglich war.

Neueste Entwicklungen der nichtlinearen Optik erlauben Lichtquellen für andere Wellenlängenregionen und mit noch größerer Bandbreite zu entwickeln (siehe Bild).

Abtastrate

In der Zeitdomäne wird das Interferenzsignal auf beliebig kleinen Intervallen abgetastet (engl. sampled). Die Abtastrate hat allerdings keinen Einfluss auf die Auflösung, die Kurve wird deshalb zwar genauer gemessen, die geringste Breite eines Einzelsignals wird aber nicht schmäler. Unterschreitet die Abtastrate allerdings die doppelte Trägerfrequenz des Signals kommt es zu Aliasing-Artefakten, gemäß dem Abtasttheorem.

Messmethoden

Signale der TD- und FD-OCT

Aufgrund der Verknüpfung der Autokorrelation (Kreuzkorrelation eines zeitlichen Signales mit sich selbst) mit dem Frequenzspektrum einer Funktion über die Fourier-Transformation, gilt im optischen Bereich die analoge Beziehung zwischen dem optischen Spektrum und dem Interferenzsignal. Deshalb spricht man einerseits vom Signal in der Zeitdomäne (englisch time domain) und andererseits vom Signal in der Frequenzdomäne (englisch frequency domain). Einfach ausgedrückt bedeutet dies, dass man entweder den Referenzarm in der Länge verändert und kontinuierlich die Intensität der Interferenz misst, ohne auf das Spektrum Rücksicht zu nehmen (time domain), oder die Interferenz der einzelnen spektralen Komponenten erfasst (frequency domain). Dieses Verfahren wurde erst durch die Verfügbarkeit von schnellen, empfindlichen Kameras und schnellen Rechnern ermöglicht.

„spatially encoded frequency domain“-OCT–Prinzip

Der Vorteil der FD-Verfahren liegt in der einfachen und schnellen simultanen Messung. Hier kann simultan die vollständige Information über die Tiefe akquiriert werden, ohne ein bewegliches Teil zu benötigen. Dies erhöht die Stabilität und die Geschwindigkeit. Man kann den Unterschied der Verfahren auch darin sehen, dass TD-OCT in jedem Messpunkt die Gesamtleistung des Referenz- und des Messarmes aufnehmen muss, dabei aber der Interferenzanteil nur einen extrem kleinen Teil ausmacht, wodurch das Rauschen des Gesamtsignals gegenüber dem Nutzanteil überwiegt. Bei Aufnahme im Frequenzbereich (FD-OCT) wird in jedem spektralen Kanal nur die entsprechende spektrale Leistung als Hintergrund gemessen. Somit gehen alle Störungen aus den anderen spektralen Bereichen verloren. Die notwendige Dynamik des Detektors sinkt mit der Gesamtleistung pro Kanal. Folglich benötigen bei gleicher Sensitivität (=Empfindlichkeit zur Messung kleinster Reflektivitäten) Frequenzdomänenmessungen nur einen Bruchteil der Leistung. FD-OCT ist meist sogar insensitiver, aber weitaus effektiver als TD-OCT.^[1] Prinzipiell ist auch eine simultane Messung in der Zeitdomäne möglich, sie erfordert aber nichtlineare Prozesse, die nur bei relativ hohen Lichtintensitäten funktionieren. Dies widerspricht aber der hochsensitiven Messung bei Messsignalleistungen unterhalb des Nanowattbereichs.

Die Fourier-Transformation arbeitet allerdings im komplexen Zahlenraum, deshalb sind beide Verfahren nur gleichwertig, wenn die komplexwertigen Funktionen bekannt sind. Das endgültige Messsignal soll aber den zeitlichen Verlauf der Reflektivität (=Absolutbetrag der Intensität in der Zeit) wiedergeben, weshalb es bei Intensitätsaufnahmen in der Frequenzdomäne und dem Fehlen der komplexwertigen Information zu Doppeldeutigkeiten kommt. Das Ergebnis ist das „Umklappen des Bildes“ beim konventionellen FD-Verfahren. Da der imaginäre Anteil einer Funktion aber einem Phasensprung um 90° entspricht, kann man durch zusätzliche Messung mit einem um 90° in der Laufzeit (also einem Viertel der Wellenlänge) verschobenen Referenzarm die komplexwertige Funktion herstellen und damit die vollständige zeitliche Funktion rekonstruieren.

Abtastrate, Linienbreite und Messtiefe

Die Abtastrate in der Frequenzdomäne ist über die Fourier-Transformation mit der Messtiefe verknüpft. Eine höhere Abtastrate, bzw. Pixelanzahl eines Detektors innerhalb des gleichen Spektralbereiches erhöht also den Bereich in dem mehrere Objekte eindeutig voneinander unterschieden werden können. Hier gilt aber wieder dieselbe Einschränkung wie in der Zeitdomäne: Wenn die Linienbreite, also die geringst mögliche spektrale Einzellinie unterschritten wird, gibt es keine zusätzliche Information beim Überabtasten mehr. (Die Linienbreite ist entweder durch die Lichtquelle beim temporal encoding, oder durch die Abbildungsgeometrie und Streueffekte im Spektrometer beim spatial encoding beschränkt). Eine größere Linienbreite als Abtastdichte führt nach der Fourier-Transformation zu einem Abfall der Objektintensität gegen den Rand des Ortsraumes. Beim Unterabtasten wiederum kommt es zur Ausbildung von Mehrfachbildern auch abseits der nullten Ordnung des Ortsbereichs, also dem Bereich, in dessen Mitte der Messarm und der Referenzarm gleich lang sind. Beim Unterabtasten werden folglich Objekte außerhalb des Messbereichs hereingespiegelt.

OCT-Messmethoden

In der letzten Zeit wurden viele unterschiedliche Methoden zur Signalerfassung entwickelt – im Folgenden ein systematischer Überblick über alle möglichen Verfahren. Die holografischen Verfahren sind das räumliche, transversale Pendant zur longitudinalen, zeitlichen Frequenzdomäne der optischen Laufzeit. Es besteht also eine Fourier-Beziehung zwischen longitudinaler Laufzeit und zeitlicher Frequenz, sowie zwischen transversaler Auslenkung und transversaler Ortsfrequenz. Prinzipiell unterscheidet man zwei Untergruppen, bei denen einerseits das Signal zeitlich kodiert wird (time encoded), also sequentiell aufgenommen wird, oder räumlich kodiert (spatially encoded), also räumlich aufgespalten, aber simultan aufgezeichnet wird. Oft werden unsystematische Bezeichnungen wie „Fourier Domain OCT“ oder „Spectral OCT“ verwendet, die aber meist verwirrend (Verwechslung mit spectroscopic OCT und ungenau – die Frequenz steht mit der Zeit in Korrelation, nicht die Wellenlänge) oder manchmal sinnentleert sind (es existiert keine Fourier-Domäne), sie sind in der Tabelle unten dennoch zur Orientierung als alternative Bezeichnungen angegeben.

Alternative Bezeichnungen im Bereich der optischen Kohärenztomografie (Übersicht)

	Time Domain (TD)		Frequency Domain (FD)
Tiefenscan	sequentiell	simultan	sequentiell	simultan
Aufwand	mechanisch hoch	elektronisch + optisch hoch	optisch + Nachverarbeitung hoch	optisch + Nachverarbeitung hoch
Lichtquelle	breitbandig	breitbandig	veränderliche Wellenlänge	breitbandig
Interferometer	Strahlteiler	aufgeweiteter Messstrahl	Strahlteiler	Strahlteiler
Scanner	verschiebbarer Referenzarmspiegel	statisch	statisch	statisch
Detektor	einfach, hochempfindlich (Diode)	Feld (Dioden, CCD oder CMOS line-array)	einfach, hochempfindlich (Diode)	komplex, Prisma oder Gitter + Feld
1D-OCT
systematische Bezeichnung	1D-teTD OCT	1D-seTD OCT	1D-teFD OCT	1D-seFD OCT
alternative Bezeichnung	scanning TD OCT	–	swept source OCT, spectral Domain OCT	'Frequency Domain OCT, Fourier (Transform) OCT, spectral Domain OCT
2D-OCT
systematische Bezeichnung	2D-teTD OCT	2D-seTD OCT	2D-teFD OCT	2D-seFD OCT
alternative Bezeichnung	–	–	–	parallel spectral Domain OCT
Parallelisierbarkeit	einfach	mittel	einfach	schwer
2D-Orientierung	en-face (normal zum Strahl)	Querschnitt (eine Achse in Strahlrichtung)	en-face	Querschnitt
3D-OCT
systematische Bezeichnung	3D-teTD OCT	3D-seTD OCT	3D-teFD OCT	3D-seFD OCT
alternative Bezeichnung	en-face OCT, full field/frame OCT	time encoded Frequency Domain OCT	–	–
Parallelisierbarkeit	einfach	–	einfach	extrem komplex
Holografische Abbildung
systematische Bezeichnung	holo-teTD-OCT	–	holo-teFD-OCT	–
alternative Bezeichnung	holographic OCT	–	holographic teFD OCT	–

Die Verfahren unterscheiden sich in ihrer Abbildungsqualität und Anwendbarkeit, bedingt durch die Verwendung verschiedener Komponenten. Speziell die FD-Verfahren haben den Vorteil kein Licht zu vergeuden und besitzen eine vielfach höhere Empfindlichkeit. Das Ziel ist eine hohe Sensitivität, bei Einsatz möglichst weniger beweglicher Komponenten und damit eine hohe Geschwindigkeit, beispielsweise 3D-teFD- und holographische Verfahren. Andererseits ist die Phasenkohärenz besser bei den potenziell langsameren Verfahren. Darüber hinaus kommt es auf die Ausrichtung der Rastermethode und deren Rasterdichte an; so wird in geschichteten biologischen Geweben üblicherweise eine hohe Rasterdichte im Tiefenquerschnitt gewünscht, die von den schnellen, einfachen on-face-Methoden nur schwer geliefert wird.

Erweiterungen

Zusätzlich zur rein topografischen Information können weitere Daten aus dem Ursprungssignal ausgewertet werden. So kann über Messung mehrerer aufeinanderfolgender Tomogramme an der gleichen Stelle die lokale Dopplerverschiebung zur Geschwindigkeitsmessung herangezogen werden (Doppler-OCT). Darüber hinaus können verschiedene Materialeigenschaften wie Streuung, Absorption, Polarisationveränderung (englisch polarisation sensitive OCT) und Dispersion ermittelt und dargestellt werden. Darüber hinaus versucht man Gewebe zu markieren oder nur selektiv nach bestimmten Molekülen zu durchsuchen (englisch molecular contrast OCT).

Vorteile

Der große technologische Vorteil der OCT ist die Entkopplung der Tiefenauflösung von der transversalen Auflösung. Im Gegensatz zur Mikroskopie kann dadurch die dreidimensionale Struktur des zu untersuchenden Gegenstandes erfasst werden. Die rein reflektive und damit berührungslose Messung erlaubt den Wegfall der in der Mikroskopie angewandten Dünnschnitte, wodurch das Verfahren mikroskopische Bilder im lebenden Gewebe (in vivo) erlaubt.

Aufgrund der hohen Selektivität des Wirkungsprinzipes können sehr kleine Signale (unterhalb von Nanowatt) detektiert und einer bestimmten Tiefe zugeordnet werden, bei geringen Eingangsleistungen. Damit eignet sich dieses Verfahren auch gut um lichtempfindliche Gewebe zu untersuchen.

Der Einsatz von OCT wird durch die wellenlängenabhängige Eindringtiefe elektromagnetischer Strahlung in das Untersuchungsobjekt sowie durch die bandbreitenabhängige Auflösung beschränkt. Hochentwickelte Breitband-Laser ermöglichen seit 1996 ^[2] die Entwicklung der UHR-OCT (UltraHigh Resolution OCT), die die Tiefenauflösung von mehreren Mikrometern bis zu Bruchteilen von Mikrometern vorangetrieben hat. Subzelluläre Strukturen in menschlichen Krebszellen können auf diese Weise dargestellt werden.

Ähnliche Verfahren

OCT ist verwandt mit anderen interferometrischen profilgebenden Verfahren (sie erlauben allerdings nur die Darstellung der Oberfläche) wie der Holografie und dem optischen Kohärenzradar, welches zur hochpräzisen dreidimensionalen Darstellung von Oberflächen im Flugzeugbau und der Autoindustrie dient. Außerdem überlappt die digitale Holographie mit dem Bereich der OCT. Hier wird das physikalische Bild in der Fourier-ebene aufgenommen und das Interferenzmuster mittels mathematischer Rückrechnung auf das gesamte Volumen erweitert. Der Vorteil hier ist die Unabhängigkeit von der Fokussierung (die numerisch kompensiert wird) nur einen Abfall in der Intensität, aber nicht durch Unschärfe. Numerische Holographie hat den Nachteil, dass sie sehr empfindlich bezüglich Speckle ist, die bei streuenden Materialien ist. Zudem kann die Holographie, so wie die „Full-Field“-OCT-Varianten nicht von dem konfokalen Vorteil zur Unterdrückung des Übersprechens profitieren. Überlapp gibt es auch bei den Phasenmodulationsverfahren, bei denen primär die Phase im Interferenzarm moduliert wird.

Ausblick

OCT ist ein relativ junges Verfahren (ursprünglich entwickelt in den späten 1980ern) und beginnt sich derzeit auf verschiedenen Gebieten zu etablieren. Auch sind noch nicht alle technischen Möglichkeiten ausgeschöpft. Die geringe Belastung des Untersuchungsobjekts, die hohe Auflösung und zunehmende Geschwindigkeit machen das Verfahren extrem attraktiv. Neue Lichtquellen, Detektoren und Scanner werden es künftig erlauben hochaufgelöste dreidimensionale Mikroskopie am Lebenden in Videogeschwindigkeit durchzuführen. Die Datenmenge für solche Aufnahmen hoher Qualität würde einige Gigavoxel pro Sekunde erreichen; derzeitige hochauflösende OCT-Verfahren erreichen bis zu 250 Megavoxel pro Sekunde, wobei der Stand im Jahre 2000 noch unterhalb von 100 Kilovoxel pro Sekunde gelegen hat. Ultrahochgeschwindigkeits-OCT mit geringerer Empfindlichkeit erreicht durch parallele Detektion bereits bis zu 60 Gigavoxel pro Sekunde.

Siehe auch

• Mikroskop
• Lichtmikroskopie
• Weißlichtinterferometer

Referenzen

1. ↑ B. Liu, M. E. Brezinski: Theoretical and practical considerations on detection performance of time domain, Fourier domain, and swept source optical coherence tomography. In: Journal of Biomedical Optics. 12, 2007, S. 044007 (doi:10.1117/1.2753410). 
2. ↑ Wolfgang Drexler, Uwe Morgner, Ravi K. Ghanta, Franz X. Kärtner, Joel S. Schuman, James G. Fujimoto: Ultrahigh-resolution ophthalmic optical coherence tomography.[erratum appears in Nat Med May 2001; 7 (5): 636.]. In: Nature Medicine. 7, Nr. 4, 2001, S. 502-507 (doi:10.1038/86589).