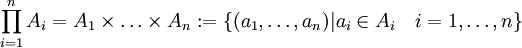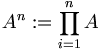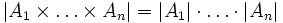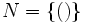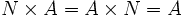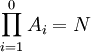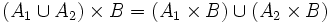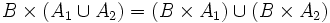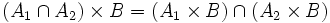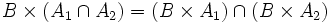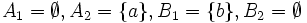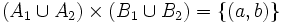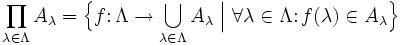- Produktmenge
-
In der Mathematik bezeichnet man als kartesisches Produkt (nach René Descartes) zweier Mengen A und B die Menge aller geordneten Paare (a,b), wobei a aus A und b aus B ist. (Kombination: „Jedes mit jedem“) Geschrieben wird es als
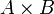 , gelesen als A kreuz B:
, gelesen als A kreuz B: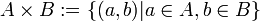 .
.
Eine Verallgemeinerung ist das kartesische Produkt von n Mengen
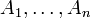 , es besteht aus allen n-Tupeln (
, es besteht aus allen n-Tupeln (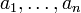 ) mit ai aus Ai, man schreibt es als
) mit ai aus Ai, man schreibt es als 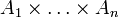 , oder als
, oder alsIst eine der Mengen Ai leer, dann ist auch das kartesische Produkt die leere Menge.
Das n-fache kartesische Produkt, bei dem alle Ai' gleich A sind, schreibt man auch als An.
Inhaltsverzeichnis
Beispiele
Sei
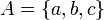 und
und 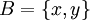 . Dann ist:
. Dann ist: 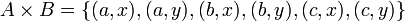 .
.Sei A = {0,1}, dann ist
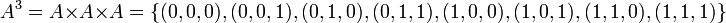 .
.Der dreidimensionale Vektorraum
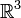 besteht aus dem dreifachen kartesischen Produkt von
besteht aus dem dreifachen kartesischen Produkt von  . Die 3-Tupel nennt man auch kartesische Koordinaten.
. Die 3-Tupel nennt man auch kartesische Koordinaten.November/Dezember 2004 W Mo Di Mi Do Fr Sa So 45 1 2 3 4 5 6 7 46 8 9 10 11 12 13 14 47 15 16 17 18 19 20 21 48 22 23 24 25 26 27 28 49 29 30 1 2 3 4 5 Ein sehr elementares nichtmathematisches Beispiel ist unser Kalender, in dem die Wochentage waagerecht nebeneinander angeordnet sind und die Wochen untereinander. Jeder einzelne Tag ist durch die Angabe seiner Kalenderwoche und des Wochentages bestimmt: Alle untereinander in einer Spalte stehenden Tage haben denselben Wochentag, alle nebeneinander in einer Zeile stehenden Tage liegen in derselben Kalenderwoche.
So ist durch die Angabe (47. Kalenderwoche 2004, Montag) der 15. November 2004 bestimmt; der 1. Dezember 2004 hat die Koordinaten (49. Kalenderwoche 2004, Mittwoch).
Eigenschaften
Anzahl der Elemente
Sind
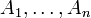 endlich viele Mengen, die alle endlich sind, dann ist auch ihr kartesisches Produkt eine endliche Menge, und die Anzahl seiner Elemente ist gleich dem Produkt der Elementanzahlen der Ai:
endlich viele Mengen, die alle endlich sind, dann ist auch ihr kartesisches Produkt eine endliche Menge, und die Anzahl seiner Elemente ist gleich dem Produkt der Elementanzahlen der Ai:Neutrales Element
Das Neutrale Element ist eine Menge, die als einziges Element das leere oder 0-Tupel enthält.
- | N | = 1
Leeres Produkt
Das kartesische Produkt von 0 Mengen ist das neutrale Element N.
Assoziativgesetz
Das kartesische Produkt ist nicht assoziativ;
enthält Paare, deren erstes Element aus A1 und deren zweites Element ein Paar aus
 ist;
ist;enthält hingegen Paare, deren erstes Element ein Paar aus
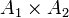 und deren zweites Element aus A3 ist. Da es aber eine kanonische Bijektion zwischen diesen Mengen gibt, kann der Unterschied zwischen
und deren zweites Element aus A3 ist. Da es aber eine kanonische Bijektion zwischen diesen Mengen gibt, kann der Unterschied zwischen 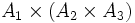 und
und 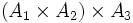 in vielen Fällen vernachlässigt werden, da er lediglich einer Notationsänderung entspricht.
in vielen Fällen vernachlässigt werden, da er lediglich einer Notationsänderung entspricht.Kommutativgesetz
Das kartesische Produkt ist auch nicht kommutativ; bei
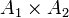 ist das erste Element aus A1 und das zweite aus A2; bei
ist das erste Element aus A1 und das zweite aus A2; bei  hingegen ist das zweite Element aus A1 und das erste aus A2. Auch hier gibt es eine kanonische Bijektion zwischen
hingegen ist das zweite Element aus A1 und das erste aus A2. Auch hier gibt es eine kanonische Bijektion zwischen 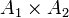 und
und  .
.Distributivgesetze
Es gelten folgende Distributivgesetze:
Sonstige Rechenregeln
Es gilt zwar
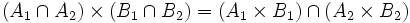 ,
,
aber es kann durchaus sein, dass
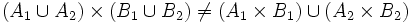 ,
,
wie z. B. am Beispiel
ersichtlich:
aber
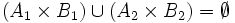 .
.
Unendliches kartesisches Produkt
Die obige Definition eines kartesischen Produkts von endlich vielen Mengen ist für viele Zwecke ausreichend. Es ist jedoch möglich, das kartesische Produkt beliebig vieler (z. B. überabzählbar vieler) Mengen zu definieren.
Ist Λ eine Menge (eine so genannte Indexmenge) und
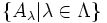 ein System von Mengen (eine so genannte Mengenfamilie), dann definiert man das kartesische Produkt der Mengen Aλ so:
ein System von Mengen (eine so genannte Mengenfamilie), dann definiert man das kartesische Produkt der Mengen Aλ so:Dies ist die Menge aller Abbildungen von Λ in die Vereinigung der Aλ, für die das Bild von λ in Aλ liegt. Für endliche Indexmengen
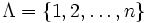 lässt sich diese Menge bijektiv auf das oben definierte Produkt abbilden, denn jedes n-Tupel
lässt sich diese Menge bijektiv auf das oben definierte Produkt abbilden, denn jedes n-Tupel 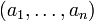 definiert eine Funktion f mit
definiert eine Funktion f mit  und umgekehrt lässt sich jede solche Funktion als Tupel
und umgekehrt lässt sich jede solche Funktion als Tupel  schreiben.
schreiben.Sind alle Aλ gleich einer Menge A, dann ist das kartesische Produkt
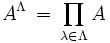 die Menge aller Funktionen von Λ nach A.
die Menge aller Funktionen von Λ nach A.
Ein besonders wichtiger und bekannter Fall ist die Indexmenge
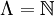 (die Menge der natürlichen Zahlen). In diesem Fall erhält man als kartesisches Produkt die Menge aller Folgen, deren i-tes Glied in der Menge Ai liegt. Sind z. B. alle
(die Menge der natürlichen Zahlen). In diesem Fall erhält man als kartesisches Produkt die Menge aller Folgen, deren i-tes Glied in der Menge Ai liegt. Sind z. B. alle 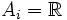 (die Menge der reellen Zahlen), dann ist
(die Menge der reellen Zahlen), dann ist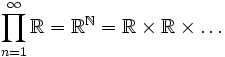 die Menge aller reellen Zahlenfolgen.
die Menge aller reellen Zahlenfolgen.
Für andere unendliche Indexmengen als N und unterschiedliche Mengen Aλ ist das kartesische Produkt weit weniger anschaulich: Bereits die Frage, ob ein beliebiges kartesisches Produkt nichtleerer Mengen nichtleer ist, ist mit der Zermelo-Fraenkel-Mengenlehre ZF nicht entscheidbar; die Behauptung, dass es nichtleer ist, ist eine Formulierung des Auswahlaxioms, welches zu ZF hinzugefügt wird, um die Mengenlehre ZFC („Zermelo-Fraenkel + Choice“) zu erhalten.
Verwandte Begriffe
Ein direktes Produkt ist ein kartesisches Produkt algebraischer Strukturen wie z. B. Gruppen, das zusätzlich mit einer komponentenweisen Verknüpfung versehen ist.
Eine direkte Summe ist eine Teilmenge des direkten Produkts, die sich nur für Produkte unendlich vieler Mengen vom direkten Produkt unterscheidet: Es besteht aus allen Tupeln, die nur an endlich vielen Stellen von einem bestimmten Element (meist dem neutralen Element einer Verknüpfung) verschieden sind.
Der Artikel Produkt (Mathematik) enthält weitere Produkt-Begriffe.
Jede Relation ist eine Teilmenge eines kartesischen Produkts.
Wikimedia Foundation.