Zentillion

In diesem Artikel geht es um den Aufbau von Zahlennamen und die Benennung von Zahlen im Dezimalsystem.

Der Aufbau von Zahlennamen

Am Beispiel der Zahl vierhundertsiebenundzwanzigtausendfünfhundertvierunddreißig (427.534) kann man den abgestuften Aufbau der Zahlennamen ersehen. Auffällig ist dabei in der deutschen Sprache die systematische Umkehrung der Zehner- und der Einerstelle, die zum Beispiel im Englischen nur von der 13 bis zur 19 vorkommt.

Null bis Neun

Die Werte der Dezimalziffern sind: Null, Eins, Zwei, Drei, Vier, Fünf, Sechs, Sieben, Acht, Neun. Der Name Null steht immer alleine; auf den anderen neun Zahlennamen baut das gesamte Namenssystem auf.

Zehn

Aus dem urgermanischen Wort tehun, das unter anderem mit griechisch deka (δεκα) und lateinisch decem verwandt ist, hat sich über althochdeutsch zehan das heutige Wort zehn entwickelt.

Elf und Zwölf als Ausnahmen

Elf und zwölf von gotisch^[1] ainlif und twalif mit der Nachsilbe -lif (= „das übrig bleibende“ oder „das darüber hinausgehende“). Auch in allen anderen germanischen Sprachen, beispielsweise im Englischen (eleven, twelve) oder Niederländischen (elf, twaalf), gibt es diese Ausnahmen. Im Französischen (onze, douze) ist dieses auf den fränkischen Einfluss zurückzuführen. Hier merkt man den früheren Ansatz für ein auf zwölf Zahlen basierendes Zahlensystem. Siehe auch Dutzend (= 12), Schock (fünf Dutzend = 60) und das Gros (zwölf Dutzend = 144).

Dreizehn bis Neunzehn

Im Gegensatz zu den Zahlen über Zwanzig, bei denen die Einerstelle und die Zehnerstelle mit einem „und“ verknüpft werden (siebenundzwanzig), entfällt dies bei den Zahlen von dreizehn bis neunzehn. Bei den Zahlen sechzehn und siebzehn wird die Einerstelle verkürzt ausgesprochen („sechzehn“ statt „sechszehn“ und „siebzehn“ statt „siebenzehn“).

Zwanzig bis Neunzig

Zwanzig: von gotisch^[1] twai tigjus (= „zwei zehn-Einheiten“), später twai tig. Diese Bildungsform setzt sich bis neunzig fort, wobei auch hier die Endsilben der sechs und der sieben verkürzt sind („sechzig“ statt „sechszig“ und „siebzig“ statt „siebenzig“).

In manchen Sprachen sind noch Reste eines Vigesimalsystems erhalten: Zum Beispiel ist im Französischen (in Frankreich und Kanada) diese Reihe nur bis 60 nach diesem Muster aufgebaut. Danach folgen „sechzig-und-zehn“ (soixante-dix), „vier-mal-zwanzig“ (quatre-vingts) und „vier-mal-zwanzig-und-zehn“ (quatre-vingt-dix). Allerdings gibt es im belgischen Französisch abweichend für 70 und 90 die Zahlworte septante und nonante und im Schweizer Französisch zusätzlich huitante und octante für 80.

Die deutsche Sprache schert, im Gegensatz zu anderen Sprachen wie der russischen, ukrainischen, englischen oder französischen, in der Reihenfolge der Zehner- und Einer-Namen aus. Wo z. B. im Englischen die Zehnereinheit zuerst kommt (twenty-five), wird im Deutschen die Einereinheit zuerst genannt (fünfundzwanzig). Weitere Sprachen, in denen Einer- und Zehnernamen wie im Deutschen gereiht werden, sind das Niederländische, das Dänische, das Luxemburgische, das Slowenische und das Arabische. Im Tschechischen sind beide Varianten möglich, d. h. „Zwanzig und eins“ oder „Einundzwanzig“.

Hunderter

Hundert: von gotisch^[1] hunda und lateinisch centum. Ursprünglich nur als Mehrzahlwort verwendet, das heißt, erst ab zweihundert. Das erste Hundert wurde noch bis ins Mittelhochdeutsche durch das Zahlwort zehan tig („zehnzig“) abgeschlossen. Heutzutage wird entweder die Hundert, oder die einfache Hundert, also Einhundert verwendet. Um ein Mehrfaches von Hundert auszudrücken, wird eine einstellige Zahl vor die Hundert angehängt. So ist der Zahlname für das dreifache von Hundert Dreihundert. Wenn das Mehrfache von Hundert größer als 9 ist, dann wechselt man meistens zum Tausender.

Für den speziellen Zahlenbereich von 1100 bis 1999, also eigentlich schon im nachfolgenden Tausenderbereich, gibt es jedoch im Deutschen – und ähnlich in diversen anderen Sprachen – die Bezeichnungen Elfhundert, Zwölfhundert bis Neunzehnhundert. Abweichend vom Deutschen wird dies im Englischen auch oft entsprechend bis zu Zahlenwerten von 9999 fortgesetzt.

Tausender

Tausend: von gotisch^[1] thusundi. Für Zahlen über Einhundert hat sich im indogermanischen Sprachraum keine einheitliche Bezeichnung entwickelt. Der Wortstamm „Tausend“ kommt nur im germanischen, slawischen und baltischen Sprachraum vor, während im romanischen die Bezeichnung von lateinisch mille hergeleitet ist und im griechischen von χιλιοι.

Million und Milliarde

Million: von lateinisch mille (= tausend) und -one (vergrößerndes Suffix); also eigentlich „Großtausend“. Die Million ist das Quadrat der Tausend.

Die Milliarde ist die dritte Potenz zur Tausend oder auch tausend Millionen.

Unterschied Europa/USA

Hauptartikel: Lange und kurze Leiter

Seit dem 17. Jahrhundert gibt es zwei unterschiedliche Konventionen für Namen großer Zahlen oberhalb der Million, die auch noch identische Zahlennamen für völlig verschiedene Zahlen verwenden. Das führt in der Praxis oft zu Missverständnissen:

• Das in diesem Artikel im Folgenden beschriebene (seit dem 15. Jahrhundert attestierte) ursprüngliche System der langen Leiter ist das anerkannte Referenzsystem. Es wird weltweit verwendet. Nur sehr wenige Länder weichen davon ab.
• Das System der kurzen Leiter, bei dem die Billion nur das 1000-fache einer Million ist. Das Tausendfache einer Billion ist dann die Trillion und so weiter. Dieses System wird in den USA, Puerto Rico, Brasilien und der Türkei verwendet, wobei aber im Sprachgebrauch der Türkei das Wort milyar für Milliarde (10⁹) fest verankert ist. Deswegen entspricht der europäischen Milliarde die US-amerikanische billion, der europäischen Billion die US-amerikanische trillion und so weiter. Das britische Englisch gleicht sich zunehmend dem US-amerikanischen Sprachgebrauch an. Im US-Englisch fehlen die Bezeichnungen auf die Endung -arde (Milliarde, Billiarde, ...); im britischen Englisch werden sie nur noch selten verwendet. Mehr zur Entstehung dieses Systems ist im Artikel Billion zu finden. Vielleicht auch wegen der möglichen Missverständnisse sind diese großen Zahlennamen jenseits der billion im täglichen Sprachgebrauch im englischen Sprachraum auch eher selten, meist greift man lieber zu Konstruktionen wie a thousand million millions.

Im veränderten System der kurzen Leiter entsprechen die Vorsilben den Potenzen der Zahl 1000, jedoch ist die lateinische Bedeutung der Vorsilbe stets um 1 zu klein – eine Billion sind also 1000³, eine Trillion 1000⁴.

Nomenklatur für Zahlen ab 1.000.000

Zahlwörter mit einem Wert von über 999.999 werden nach dem System von Nicolas Chuquet nach lateinischen Präfixen benannt. Eine Ausnahme stellt dafür das Zahlwort Million dar. Dieses leitet sich vom lateinischen mille (1000) ab. Die Nicht-Kombinationspräfixe, also Präfixe, die nicht in Kombinationen mit anderen Präfixen auftauchen (abgesehen bei der Bildung der Präfixe mit einem Wert von über 999), leiten sich von lateinischen Ordinalzahlen ab. Die Kombinationspräfixe leiten sich von lateinischen Kardinalzahlen ab.

Einer (Nicht-Kombinationspräfixe):
1 - mi
2 - bi
3 - tri
4 - quadri
5 - quinti
6 - sexti
7 - septi
8 - okti
9 - noni

Einer (Kombinations-Präfixe):
1 - un
2 - duo
3 - tre(s)
4 - quattuor
5 - quinqua
6 - se(s)(x)
7 - septe(m)(n)
8 - okto
9 - nove(m)(n)

Zehner:
10 - (n)dezi
20 - (m)(s)viginti
30 - (n)(s)triginta
40 - (n)(s)quadraginta
50 - (n)(s)quinquaginta
60 - (n)sexaginta
70 - (n)septuaginta
80 - (m)(x)oktoginta
90 - nonaginta

Hunderter:
100 - (n)(x)zenti
200 - (n)duzenti
300 - (n)(s)trezenti
400 - (n)(s)quadringenti
500 - (n)(s)quingenti
600 - (n)seszenti
700 - (n)septingenti
800 - (m)(x)oktingenti
900 - nongenti

Kombinieren lassen sich die Präfixe nach dieser Reihenfolge: Einer+Zehner+Hunderter.

Steht vor einem Zehner- oder Hunderter-Präfix z. B. ein eingeklammertes M, bedeutet das, dass man dieses M bei der Kombination mit einem Einer-Präfix, bei welchem auch dieses eingeklammerte M dabei ist, zu dem Einer-Präfix anfügen soll (das eingeklammerte M im Zehner- oder Hunderter-Präfix kommt weg). - Dies gilt auch für alle anderen eingeklammerten Buchstaben.

Beispiele:

• Tres-zenti
• Septem-oktoginta-zenti
• Sex-zenti

Dabei gibt es eine Ausnahme:

• Es heißt nicht Quinquadezillion, sondern Quindezillion.

Um aus diesen Präfixen ein Zahlwort zu bilden, muss man die Endung -llion anfügen. Die gebildete Zahl entspricht 10ⁿ⁶ (n steht dabei für den Wert des gebildeten Präfixes; z.B. treszenti- = 103). Hängt man zu dem Präfix die Endung -lliarde dran (nach Jacques Pelletier du Mans), wird die Nullenanzahl um 3 Nullen größer, als die Nullenanzahl des Zahlwortes mit der Endung -llion.

Beispiel:

• Zentillion = 10^100*6 = 10⁶⁰⁰
• Zentilliarde = 10⁶⁰⁰⁺³

Falls man ein Zehner-Präfix nimmt, ohne diesen mit einem Hunderter-Präfix zu kombinieren, muss man die Endung -a (falls vorhanden) durch -i ersetzen.

Beispiel:

• Triginta → triginti- → Trigintillion (10^30*6 = 10¹⁸⁰).

Die Bildung der Präfixe mit einem Wert von über 999 funktioniert so:

Falls man ein z.B. Zahlwort mit dem Wert 10⁶⁰⁰⁰ bilden will, teilt man die Hochzahl der Potenz durch 6: 1000.

Nun trennt man die Zahl in 3er-Gruppen: 1_000

Das Zahlwort dafür lautet folglich: Millinillion.

Erklärung: Mi- ist ein Nicht-Kombinationspräfix und steht für 1. lli- gilt als Abstand für die nächste 3er-Gruppe. ni- steht für Tausender (falls es allein steht, dann ohne eine bestimmte Anzahl). -llion ist die Endung die man dranfügen soll, damit aus dem Präfix ein Zahlwort wird. Folglich lautet das Zahlwort: Mi-lli-ni-llion.

Weitere Beispiele:

• Noni-lli-nove-nonaginta-nongenti-llion = 10⁵⁹⁹⁹⁴
• Okti-lli-okto-oktoginta-oktingenti-llion = 10⁵³³²⁸
• Quinti-lli-quinqua-quinquaginta-quingenti-llion = 10³³³³⁰

Dieses System geht auf John Horton Conway und Allan Wechsler zurück.^[2]

Synonyme

• Sexdezillion ^[3] = Sedezillion
• Novemdezillion ^[4] = Novendezillion
• Quinquillion ^[5] = Quintillion

Nach dem System von Nicolas Chuquet kann man von (spät)lateinischen Zahlwörtern folgende Präfixe herleiten:

18 - duodeviginti
19 - undeviginti
28 - duodetriginta
29 - undetriginta
38 - duodequadraginta
39 - undequadraginta
48 - duodequinquaginta
49 - undequinquaginta
58 - duodesexaginta
59 - undesexaginta
68 - duodeseptuaginta
69 - undeseptuaginta
78 - duodeoctoginta
79 - undeoctoginta
88 - duodenonaginta
89 - undenonaginta
98 - duodecenti
99 - undecenti^[6]

Das amerikanische System

Im amerikanischen System werden Zahlwörter mit der Endung -lliarde (oder in der engl. Form -lliard) übersprungen. Eine Milliarde ist im amerikanischen System daher eine Billion. Eine Billion ist im amerikanischen System eine Trillion, eine Billiarde ist im amerikanischen System eine Quadrillion und so weiter.

In ganz Europa funktioniert das System genau so, wie oben bereits beschrieben.

Abkürzungen

Die folgenden Abkürzungen sind in der deutschen Sprache gültig:

• Mio. = Million
• Mill. = Million/Millionär
• Mrd./Mia./Md. = Milliarde
• Bio./Bill. = Billion^[7]

Zusammenstellung der Unregelmäßigkeiten

Zahlen bis 1.000.000

• Es heißt elf, zwölf anstatt einszehn, zweizehn (bzw. zehneins, zehnzwei).
• Bei sechzehn und siebzehn sowie sechzig und siebzig ist die Einersilbe verkürzt.
• Es heißt zwanzig anstatt zweizig.
• Zahlen wie z. B. einundzwanzig sind mit „und“ verknüpft.
• Bei einer Zahlenzusammensetzung mit eins-, also eins und zwanzig, muss das s gestrichen werden. Für Zahlenzusammensetzungen mit sechs- gilt dies nicht.
• Man verwendet die Nachsilbe -zig anstatt -zehn.
• Die Nachsilbe -ßig bei dreißig anstelle von -zig stellt eine Ausnahme dar.
• Es wird erst die Hunderter-, dann die Einer- und dann die Zehnersilbe genannt.
• Es wird das Dezimalsystem^[8] verwendet.

Zahlen ab 1.000.000

• Es heißt Quindezillion anstatt Quinquadezillion.
• 10 hoch 100 heißt Googol.

Brüche

Bruchzahlen werden mit den Ordinalzahlen und dem Suffix –el gebildet (drittel, viertel, fünftel, usw.).

Die Begriffe eintel (anstatt ganz) und zweitel (anstatt halb) sind oft nur in mathematischen Ausdrücken gebräuchlich.

Bruchzahlen als Adjektive können auch substantiviert werden. Beispiel: zwei Zweitel sind gleich ein Eintel

Siehe auch

• Zahlensystem
• Römische Ziffern
• Numerologie
• Vorsätze für Maßeinheiten
• Zahlwort
• Schreibweise von Zahlen
• Zahlen in unterschiedlichen Sprachen
• Liste besonderer Zahlen
• Verein Zwanzigeins

Weblinks

• Wandelt Zahlen (in Ziffern) in Zahlwörter um (französisch)
• Informatikjahr 2006, 4. Algorithmus der Woche: Zahlen auf Deutsch aussprechen
• Zahlennahmen in USA und Europa

Einzelnachweise

1. ↑ ^{a b c d} Die Formulierung „von gotisch ...“ ist hier als Kurzform von „aus dem Germanischen, verwandt mit gotisch ...“ zu verstehen.
2. ↑ The Book of Numbers
3. ↑ http://www.merriam-webster.com/dictionary/sexdecillion
4. ↑ http://www.merriam-webster.com/dictionary/novemdecillion
5. ↑ Duden - Deutsches Universalwörterbuch + Ableitung von lateinischen Kardinalzahlen
6. ↑ http://www.arndt-bruenner.de/mathe/scripts/numeraliatab.htm
7. ↑ Duden - Deutsches Universalwörterbuch
8. ↑ Ein Computer verwendet bei seinen internen Berechnungen nicht das Dezimalsystem, sondern das Dualsystem. Das Zweiersystem hat aber den Nachteil, dass für die Darstellung einer Zahl viele Ziffern benötigt werden. Je größer die Basis b des b-adischen Stellenwertsystems ist, desto weniger Ziffern benötigt man zur Darstellung einer Zahl. Unter diesem Aspekt wäre es sinnvoll, b möglichst groß zu wählen. Wichtiger für die Frage, wie schnell man damit rechnen kann, ist allerdings, ob b viele Teiler hat oder nicht. Das Dezimalsystem mit 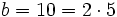$b=10=2\cdot 5$ stellt somit einen Kompromiss dar, welcher nicht unbedingt für alle Fälle der beste sein muss.