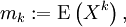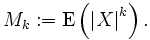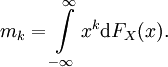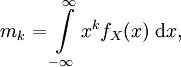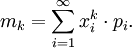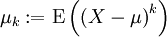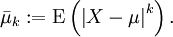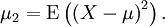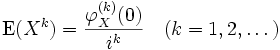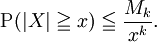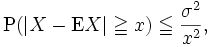- Zentrales Moment
-
Momente sind Kenngrößen von Zufallsvariablen. Sie sind Parameter der deskriptiven Statistik und spielen eine theoretische Rolle in der Stochastik. Die Begriffe Erwartungswert, Varianz, Schiefe und Wölbung zur Beschreibung einer Zufallsvariablen hängen eng mit deren Momenten zusammen.
Eine Verteilungsfunktion ist durch Angabe aller ihrer Momente bestimmt, falls diese existieren und die Reihe der momenterzeugenden Funktion konvergiert. Es gibt Verteilungen, deren Momente nur bis zu einer bestimmten Ordnung existieren. Dazu gehören die t-Verteilungen, deren Momente nur für Ordnungen existieren, die kleiner als der Freiheitsgrad sind. Im Spezialfall der Cauchy-Verteilung existiert also nicht einmal das erste Moment (der Erwartungswert), das ist auch bei der Lévy-Verteilung der Fall.
Inhaltsverzeichnis
Definition
Es sei X eine Zufallsvariable und k eine natürliche Zahl. Dann bezeichnet man als Moment der Ordnung k von X oder kürzer als k-tes Moment von X den Erwartungswert der k-ten Potenz von X (unter der Voraussetzung, dass dieser existiert):
und als k-tes absolutes Moment von X wird der Erwartungswert der k-ten Potenz des Absolutbetrages | X | von X bezeichnet:
In theoretischen Untersuchungen werden mitunter auch Momente nichtganzzahliger Ordnung κ betrachtet.
Die Existenz von Momenten einer bestimmten Ordnung liefert allgemein Aussagen über die Verteilung der Wahrscheinlichkeitsmasse.
Das erste Moment ist der Erwartungswert. Er wird meist mit μ bezeichnet und kann als Mittelwert oder „Zentralwert“ angesehen werden.
Darstellung für reelle Zufallsvariable
Ist X eine reelle Zufallsvariable mit der Verteilungsfunktion FX, dann folgt aus der Definition des Erwartungswertes
Ist X eine stetige Zufallsvariable mit der Dichtefunktion fX, dann gilt
und für eine diskrete Zufallsvariable mit Sprungpunkten xi und den Einzelwahrscheinlichkeiten pi ist
Zentrale Momente
Neben den oben definierten Momenten werden die zentralen Momente definiert, bei denen die Verteilung der Wahrscheinlichkeitsmasse um den Erwartungswert μ = E(X) der Zufallsvariablen X betrachtet wird:
und
Das zweite zentrale Moment ist die Varianz:
Das dritte zentrale Moment ist nach Normierung die Schiefe. Das vierte zentrale Moment ist nach Normierung die Wölbung (Kurtosis und Exzess). Schiefe und Wölbung werden zusammen als höhere Momente bezeichnet und oft als Maß der Abweichung von der Normalverteilung benutzt.
Momente und charakteristische Funktion
Durch mehrfaches Ableiten der Formel für die charakteristische Funktion erhält man eine Darstellung der gewöhnlichen Momente durch die charakteristische Funktion als
Das k-te Moment kann auch mit der momenterzeugenden Funktion ermittelt werden.
Markow-Ungleichung
Die Bedeutung der Momente wird durch folgenden Satz deutlich:
Wenn das k-te absolute Moment Mk der Zufallsvariablen X existiert, dann gilt
Das ist die Markow-Ungleichung, die eine Aussage über die Wahrscheinlichkeit betragsmäßig großer Werte von X liefert. Im Spezialfall k = 2 folgt daraus mit der Varianz σ2 von X die bekannte Tschebyschow-Ungleichung
die eine Aussage über die Wahrscheinlichkeit großer Abweichungen der Zufallsvariablen X von ihrem Erwartungswert macht.
Verbundmomente
Der Momentenbegriff lässt sich auch auf mehrere Zufallsvariablen erweitern. Im Falle zweier Zufallsvariablen X und Y sind die zentralen gemeinsamen Momente (engl. joint moments) von X − ηX und Y − ηY
mit
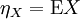 und
und 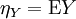 .
.Insbesondere ist μ11 die Kovarianz von X und Y.
Literatur
- Athanasios Papoulis, S. Unnikrishna Pillai: Probability, Random Variables, and Stochastic Processes. McGraw-Hill Publishing Co.; 4Rev Ed edition (2002), ISBN 0-07-366011-6.
Wikimedia Foundation.