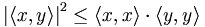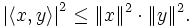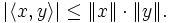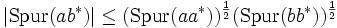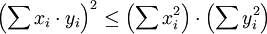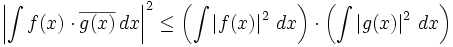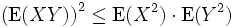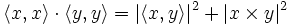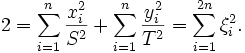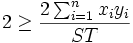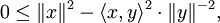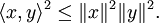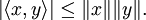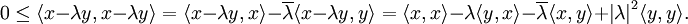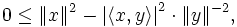- Cauchy-Schwarz Abschätzung
-
Die Cauchy-Schwarz-Ungleichung, auch bekannt als schwarzsche Ungleichung oder Cauchy-Bunjakowski-Schwarz-Ungleichung, ist eine nützliche Ungleichung, die in vielen Bereichen der Mathematik verwendet wird, z. B. in der Linearen Algebra (Vektoren), in der Analysis (unendliche Reihen), in der Wahrscheinlichkeitstheorie sowie bei Integration von Produkten. Außerdem spielt sie in der Quantenmechanik eine wichtige Rolle, wie etwa beim Beweis der Unschärferelation.
Inhaltsverzeichnis
Allgemeiner Fall
Die Ungleichung sagt aus: Wenn x und y Elemente eines reellen oder komplexen Vektorraums mit innerem Produkt sind, dann gilt für das Skalarprodukt bzw. das innere Produkt
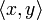 die Beziehung
die BeziehungUnter Verwendung der Norm
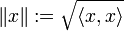 ergibt sich daraus
ergibt sich darausEs kann auch auf beiden Seiten die Wurzel gezogen werden. Man erhält, da Norm und Betrag nicht negativ sind:
Beide Seiten sind genau dann gleich, wenn x und y linear abhängig sind.
Spezialfälle
Auf quadratische Matrizen angewandt, erhält man für die Spur:
Auf euklidische Räume
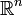 angewandt, erhält man:
angewandt, erhält man:Im Fall quadratisch integrierbarer komplexwertiger Funktionen erhält man:
Für quadratisch integrierbare Zufallsvariablen erhält man:
Die letzten drei Ungleichungen werden durch die Hölder-Ungleichung verallgemeinert.
Im
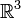 lässt sich die Cauchy-Schwarzsche Ungleichung zu einer Gleichung verschärfen:
lässt sich die Cauchy-Schwarzsche Ungleichung zu einer Gleichung verschärfen:Geschichte
Benannt ist die Ungleichung nach Augustin Louis Cauchy, Wiktor Jakowlewitsch Bunjakowski und Hermann Amandus Schwarz. Bei Cauchy findet sich die Summenform der Ungleichung in seiner Analyse algébrique (1821)[1]. Die Integralform der Ungleichung wurde historisch erstmals 1859 von Bunjakowski in einer Arbeit über Ungleichungen zwischen Integralen veröffentlicht; Schwarz veröffentlichte seine Arbeit erst 50 Jahre später.
Anwendungen
In einem Vektorraum mit innerem Produkt lässt sich aus der Cauchy-Schwarzschen Ungleichung die Dreiecksungleichung für
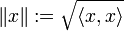 ableiten, und damit in weiterer Folge zeigen, dass durch das innere Produkt eine Norm definiert wird.
ableiten, und damit in weiterer Folge zeigen, dass durch das innere Produkt eine Norm definiert wird.Eine weitere Folgerung der Cauchy-Schwarz-Ungleichung ist, dass das innere Produkt eine stetige Funktion ist.
Die Cauchy-Schwarz-Ungleichung stellt sicher, dass im Ausdruck
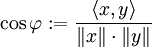 der Betrag des Bruches stets kleiner oder gleich eins ist, sodass also
der Betrag des Bruches stets kleiner oder gleich eins ist, sodass also 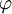 wohldefiniert ist und damit der Winkel auf beliebige Räume mit innerem Produkt verallgemeinert werden kann.
wohldefiniert ist und damit der Winkel auf beliebige Räume mit innerem Produkt verallgemeinert werden kann.In der Physik wird die Cauchy-Schwarzsche Ungleichung bei der Herleitung der Heisenbergschen Unschärferelation verwendet.
Beweis der Ungleichung
Beweis aus der Ungleichung vom arithmetischen und geometrischen Mittel
Ein Beweis der Cauchy-Schwarzschen Ungleichung kann beispielsweise mit Hilfe der Ungleichung vom arithmetischen und geometrischen Mittel erfolgen:
Definiert man für
 die Werte
die Werte  und
und  , so ergibt sich aus der Ungleichung vom arithmetischen und geometrischen Mittel die Beziehung
, so ergibt sich aus der Ungleichung vom arithmetischen und geometrischen Mittel die BeziehungDaraus folgt unmittelbar die Cauchy-Schwarzsche Ungleichung.
Beweis aus der Umordnungs-Ungleichung
Ein anderer Beweis der Cauchy-Schwarzschen Ungleichung ergibt sich aus der Umordnungs-Ungleichung. Setzt man
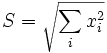 und
und 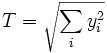 sowie
sowie 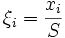 und
und 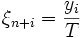 so gilt
so giltWegen der Umordnungs-Ungleichung ist nun
Zusammengefasst erhält man also
wobei dieses Ergebnis der Cauchy-Schwarzschen Ungleichung entspricht.
Beweis für das Skalarprodukt
Die oben angegebenen Beweise beweisen nur den Spezialfall der Cauchy-Schwarzsche Ungleichung in euklidischen Räumen. Der Beweis für den allgemeinen Fall des Skalarprodukts in einem Vektorraum mit innerem Produkt ist aber simpel.
Reeller Fall
Der Fall y = 0 ist einfach zu behandeln, es sei also
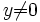 und damit
und damit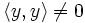 . Für jedes
. Für jedes 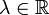 gilt
giltWählt man nun speziell
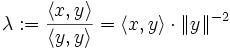 so ergibt sich
so ergibt sichalso
Ziehen der Quadratwurzel ergibt nun genau die Cauchy-Schwarzsche Ungleichung
Komplexer Fall
Der Beweis im komplexen Fall verläuft ähnlich, allerdings ist zu beachten, dass das Skalarprodukt in diesem Fall keine Linearform, sondern eine Hermitesche Form ist. Der Beweis wird für die Variante linear im ersten und semilinear im zweiten Argument geführt; wird die umgekehrte Variante gewählt, so ist an den entsprechenden Stellen die komplex Konjugierte zu nehmen.
Für jedes
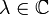 gilt
giltHier führt nun die spezielle Wahl
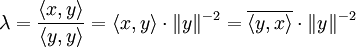 auf
aufalso
Quellen
Weblinks
Literatur
- Peter Schreiber: The Cauchy-Bunyakovsky-Schwarz inequality, in: Ders.: Hermann Grassmann, Werk und Wirkung. Internationale Fachtagung anläßlich des 150. Jahrestages des ersten Erscheinens der "linearen Ausdehnungslehre", Universität Greifswald, 1995, S. 64-70
Wikimedia Foundation.