Spiel mit perfekter Information

In der Spieltheorie ist ein Spiel mit perfekter Information ein Spiel mit vollständiger Information. Bei letzterem gibt es keine verdeckten Elemente wie unquantifizierbare Zufälle, unbekannte Karten des Gegners, gleichzeitige Züge beider Seiten o. Ä.. Zusätzlich wird bei ersterem gefordert, dass es überhaupt keine Zufallselemente gibt und alle Spieler alle Spielzüge kennen, die stattgefunden haben.

Solche Spiele sind glückselementlose Spiele wie etwa Go, Schach, Dame, Mühle, Nim und Mancala als Zweipersonenspiele oder auch Solitär und SameGame als Solitairespiel. Wenn diese Spiele endlich sind, gibt es – zumindest theoretisch – für einen der beiden Spieler immer eine Remisstrategie, die unentschiedene Endstellungen herbeiführt oder Spielsituationen beliebig oft wiederholt, oder eine Gewinnstrategie, falls die Regeln ein Unentschieden nicht zulassen.

Spiele, die nicht endlich sind oder nicht terminieren, sprengen den Rahmen dieses Artikels.

Je nach Komplexität des Spiels kann die tatsächliche Ermittlung des besten oder auch nur eines guten Zuges sehr schwierig sein. Zahlreiche Spiele, darunter Dame, Mühle und Vier gewinnt, sind mittlerweile vollständig gelöst und die entsprechenden Strategien sind bekannt.

Abgrenzung

Im Gegensatz zu oben genannten Spielen sind etwa Schiffe versenken, Mastermind und die meisten Kartenspiele keine Spiele mit perfekter Information. Auch ein Spiel wie Schere, Stein, Papier ist kein Spiel mit perfekter Information, da der zentrale gleichzeitige Zug des Mitspielers für den Spieler nicht bekannt ist. In diesen Fällen lässt sich lediglich eine „riskante“ Entscheidung zum Beispiel aufgrund von Wahrscheinlichkeiten treffen, weil nicht alle erforderlichen Informationen verfügbar sind.

Auch die Spiele mit vollständiger Information und Zufallselementen wie (Mensch ärgere Dich nicht und Backgammon) rechnet man zu den Spielen mit perfekter Information, obwohl das konkret eintreffende Ergebnis vom Zufall abhängt.

Bei Problemen der Wirtschaft, die vielfach mit spieltheoretischen Ansätzen untersucht wurden und werden, begegnet man fast ausschließlich Spielen ohne perfekte, ja nicht einmal vollständige Information, da zum Beispiel wirtschaftliche Eckdaten und Planungen von konkurrierenden Unternehmen im Allgemeinen nicht bekannt sind.

Beispiele für Spiele mit 2 Spielern ohne Unentschieden

Eins oder zwei

Das folgende Streichholzspiel ist eines der einfachsten:

Zwischen zwei Spielern liegt ein Haufen Streichhölzer. Beide Spieler nehmen abwechselnd ein Holz oder zwei Hölzer. Wer das letzte Holz nimmt, gewinnt (siehe Eins oder zwei).

Das Spiel von Professeur Rufus Isaacs

Im Spiel von Professeur Rufus Isaacs (zitiert aus Berge^[1]) markieren die Spieler im I. Quadranten der Ebene mit ganzzahligem Gitter (in Formeln $\mathbb{N}_0 \times \mathbb{N}_0$) abwechselnd einen Knoten, wobei sich der Nachfolgeknoten vom Vorgängerknoten aus gesehen auf einer gleichen Koordinate (waagerecht oder senkrecht) oder der Winkelhalbierenden jeweils in Richtung Ursprung befinden muss. Der Spieler, der als Erster den Ursprung erreicht, hat gewonnen. Die Anfangsstellung wird ausgelost.

Nim

Beim Nim-Spiel sind mehrere Reihen mit Streichhölzern vorhanden. Zwei Spieler nehmen abwechselnd Streichhölzer aus einer der Reihen weg. Wie viele sie nehmen, spielt keine Rolle; es muss mindestens ein Streichholz sein und es dürfen bei einem Zug nur Streichhölzer einer einzigen Reihe genommen werden. Derjenige Spieler, der den letzten Zug macht – also die letzten Streichhölzer wegnimmt – gewinnt.

→ Hauptartikel: Nim-Spiel

Andere Gewinnregel

Der Spieler, der den letzten Zug macht (das letzte Streichholz nimmt), hat nicht gewonnen, sondern verloren. Diese Regel heißt Misère-Regel.

Das Nim-Spiel Marienbad, das durch den Film Letztes Jahr in Marienbad von Alain Resnais bekannt wurde, ist eine Misère-Variante.

Strategie

Wie bei allen schrumpfenden Spielen mit perfekter Information ohne Unentschieden für zwei Spieler gibt es zwei Kategorien von Spielstellungen (wenn man von einer Endstellung des Spiels zunächst absieht):

1. die Z-Stellung (von „Zwang“): Aus einer Z-Stellung muss immer eine C-Stellung gemacht werden.
2. die C-Stellung (von „Chance“): Aus einer C-Stellung kann immer eine Z-Stellung gemacht werden.

Graphentheoretische Charakterisierung

Die Stellungen lassen sich in einem gerichteten Graphen darstellen mit Knoten für die Stellungen und Bögen (gerichteten Kanten) für die möglichen Züge. D. h. ein einzelner möglicher Zug wird durch einen Bogen repräsentiert, der von einer direkten Vorgänger-Stellung $u \,$ zu einer direkten Nachfolger-Stellung $v \,$ führt, in Zeichen $u\rightarrow v$. (Z. B. bettet man bei Nim in naheliegender Weise diesen Graphen in das $\, n$-dimensionale ${ \color{Blue} \big( [0, r_1] \times [0, r_2] \times ... \times [0, r_n] \big)}$-Intervall der Stellungen ein, wo $n \,$ die Anzahl der Reihen ist und $r_i \,$ die Anzahl der Streichhölzer in der $\, i$-ten Reihe. Eine Spielstellung entspricht dann einem Knoten mit den momentanen Anzahlen von Streichhölzern als seinen Koordinaten. Die möglichen Züge (Bögen) sind parallel zu genau 1 Koordinate mit Richtung auf den Ursprung zu.)

Die eingangs aufgestellte Forderung nach Endlichkeit ist nur durch die Zyklenfreiheit des Stellungsgraphen erfüllbar. (Regelungen etwa für dreimalige Zugwiederholung können durch entsprechende Expansion des Graphen gelöst werden.) Seine transitive Hülle ist somit eine Halbordnung $\lessdot$, wo $u\lessdot v$ bedeutet, dass es einen gerichteten Weg von $u \,$ nach $v \,$ gibt,d. h. $m \; (\ge 0)$ Zwischenknoten $w_1, ... , w_m \,$ und Zwischenzüge mit $u\rightarrow w_1\rightarrow ... \rightarrow w_m\rightarrow v$.

Die Strategie beruht nun auf folgender These:

Die Knoten im Graphen lassen sich entsprechend ihrer Kategorie in genau 2 Farben einfärben, z. B. die Z-Knoten grün und die C-Knoten rot. Und es gibt von einem C-Knoten immer und von einem Z-Knoten nie einen Bogen zu einem Z-Knoten.

Bevor wir den von dieser These nahe gelegten Algorithmus formulieren, nehmen wir an dem Graphen noch folgende Änderung vor:

• Das Spiel soll zu Ende sein, wenn ein Spieler nicht mehr ziehen kann. Dieser soll dann auch der Verlierer sein. Eine Misère-Endstellung (bei der der Spieler, der nicht mehr ziehen kann, gewinnt) lösen wir, indem wir an sie genau einen Bogen zu einem zusätzlichen Knoten hinzufügen, welchen Zug der Gewinner abschließend virtuell noch auszuführen hat.

Wir betten die Halbordnung $\lessdot$ in eine lineare (totale) Ordnung ein und benennen diese wieder mit $\lessdot$. (Wegen des Einbettens siehe lineare Erweiterung einer Halbordnung in der englischen Wikipedia.) Wenn also $v \,$ eine Stellung ist, die nach einer gewesenen Stellung $u \,$ entstehen kann, dann gilt $u \lessdot v$ sowohl in der Halbordnung wie in der Totalordnung.

Wir beginnen beim Maximum der Totalordnung (es muss eine Senke und Endstellung sein – die bei Nim, aber auch sonst häufig mit dem Ursprung zusammenfällt) und arbeiten den Stellungsraum (quasi „kausal rückwärts“) die gewählte Totalordnung absteigend und schrittweise in Richtung Minimum ab. Dadurch ist sichergestellt, dass wir den ganzen Raum absuchen und in keine Schleife geraten. Schon eingefärbte Knoten bleiben ungeändert, und auch sonst ist bei ihnen keine Aktion erforderlich.

Kommen wir zu einem ungefärbten Knoten $v \,$, dann müssen seine direkten Nachfolger $w \; (\leftarrow v)$ alle rot sein. Wäre nämlich ein grüner $w \,$ dabei, hätte $v \,$ von $w \,$ aus wegen $w \leftarrow v$ schon rot gefärbt worden sein müssen (s. u.); und ein ungefärbtes $w \,$ wäre in der absteigenden Totalordnung wegen $w \gtrdot v$ vor $v \,$ an der Reihe gewesen. Das Ergebnis: Der Z-Knoten $v \,$ hat nur C-Knoten $w \,$ als direkte Nachfolger.

Die direkten Vorgänger $u \,$ (also $v \leftarrow u$) können nur ungefärbt oder rot sein, denn ein grünes $u \,$ wäre vor $v \; (\gtrdot u)$ gefärbt worden entgegen der absteigenden Totalordnung. Der Knoten $v \,$ wird nun grün gefärbt und alle seine direkten Vorgänger $u \,$ werden rot gefärbt. Das Ergebnis: Da die Umfärbung von $u \,$ auf rot immer nur von einem grünen Knoten $v \,$ aus geschieht, können wir von einem C-Knoten $u \,$ immer in einem Zug zu einem Z-Knoten $v \,$ kommen.

Gibt es keinen ungefärbten Knoten mehr, terminiert der Algorithmus.

Aus Sicht des Graphentheoretikers haben wir zu einem Graphen einen Kern konstruiert, d. i. eine stabile Untermenge von Knoten, die gleichzeitig dominierend ist.^[2] Der Kern ist die Menge der Z-Knoten. Die Stabilität steht für den Zwang, von einem Z-Knoten zu einem C-Knoten gehen zu müssen, und die Dominanz für die Chance, von einem C-Knoten zu einem Z-Knoten gehen zu können.

Eins oder zwei

Auch das triviale Spiel Eins oder zwei, dessen optimale Strategie auch ohne viel Mathematik sofort zu verstehen ist, lässt sich mit dem obigen Algorithmus behandeln: Der Stellungsraum ist $\mathbb{N}_0$, die Halbgerade der nicht-negativen ganzen Zahlen.

„Kern“ des Spiels von Professeur Rufus Isaacs

Spiel von Professeur Rufus Isaacs

Beim Spiel von Professeur Rufus Isaacs kommen die Eigenschaften des Kerns gut heraus. Die Skizze der Spielregel in schwarz in der unteren rechten Ecke symbolisiert eine Art „Zukunftslichtkegel“, dem die „Vergangenheitslichtkegel“ entsprechen, die von den Z-Knoten (grün) ausgehen. Wird ein C-Knoten (rot) als Anfangsstellung ausgelost, kann der anziehende Spieler den Sieg erzwingen. Bei einem Z-Knoten (grün) als Anfangsstellung kann der Anziehende nur einen C-Knoten erreichen, wonach sein Gegenspieler den Sieg erzwingen kann.

2 kolorierte Stellungsräume des Nim-Spiels mit 3 Reihen

Nim

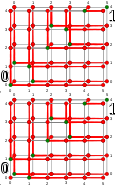
Die Graphik rechts zeigt in 2 Diagrammen die Z-Stellungen (grüne Knoten) und die C-Stellungen (rote Knoten) für die Standard- (oben) und die Misère-Regel (unten) des Nim-Spiels – jeweils der Einfachheit halber bei einem Definitionsbereich von 3 Reihen (Achsen) zu 5, 4 und 1 Streichhölzern. In beiden Diagrammen ist die Reihe mit 1 Streichholz durch 2 übereinanderliegende Ebenen, die 0- und die 1-Ebene dargestellt, so dass die 0-Ebene effektiv dem Fehlen der dritten Reihe und die 1-Ebene dem Vorhandensein 1 Streichholzes in dieser Reihe entspricht.

Der Ursprung (0,0,0) befindet sich jeweils links unten vorn.

Gültige Züge sind im Graphen Bewegungen auf genau einer der Koordinatenachsen, d. h. entweder waagerecht oder senkrecht oder auch in der dritten Richtung von der 1-Ebene auf die 0-Ebene, jeweils näher zum Ursprung hin.

Der Algorithmus beginnt am Ursprung, der bei der Standard-Regel grün, bei der Misère-Regel rot eingefärbt wird.

Es fällt auf, dass zwischen den 2 Nim-Varianten sich die Farben nur bei den Knoten ganz nahe am Ursprung unterscheiden.

Die Gewinnstrategie bei 2 Reihen für die Standard-Regel lautet: Ziehe mit deinem Gegenspieler gleich. Bei 3 und mehr Reihen wird es komplizierter, wie schon die 1-Ebenen andeutungsweise zeigen. Die allgemeineren Fälle sind noch schwieriger darzustellen.

Numerische Charakterisierung

Eins oder zwei

Die Z-Knoten beim Spiel Eins oder zwei sind genau die Knoten, deren Abszisse durch 3 teilbar ist.

Spiel von Professeur Rufus Isaacs

Beim Spiel von Professeur Rufus Isaacs sind die Z-Knoten symmetrisch zur Winkelhalbierenden angeordnet und liegen für $n \ge 0 \,$ auf den Koordinaten $\big( \lfloor n \Phi^2 \rfloor,\lfloor n \Phi \rfloor \big)$ mit $\Phi:=(1+\sqrt 5)/2$  (Zahl des goldenen Schnitts).

Durch die Irrationalität von $\Phi \,$ ergibt sich eine aperiodische unregelmäßige Verteilung.

Nim

Bezgl. der Formeln für die Nim-Summen des Nim-Spiels und des Beweises ihrer Optimalität sei auf den Hauptartikel Nim-Spiel verwiesen. Die Z-Knoten des Graphen entsprechen allesamt Z-Stellungen, wie sie mit den Nim-Summen berechnet werden können. Letztere kommen erst bei einer Anzahl > 2 von Reihen, d. h. der Komposition mehrerer „Spiele“, richtig zur Geltung. In einer 2-dimensionalen Graphik ist das jedoch nur sehr schwer deutlich zu machen.

Fazit

Die Beispiele zeigen, dass derselbe graphentheoretische Algorithmus sehr unterschiedliche formelmäßige Ergebnisse zeitigen kann. Die Graphen sind naturgemäß stets endlich und damit zwar für den „Hausgebrauch“ des Spielers ggf. ausreichend. Sie liefern auch gute Anhaltspunkte für die numerischen Formeln. Von der mathematischen Warte aus sind die Formeln aber auf höheren Rängen anzusiedeln und bedürfen auch eines speziell auf sie zugeschnittenen Beweises.

Offensichtlich ist es nicht interessant, eines dieser Spiele zu spielen, wenn beide Spieler die optimale Strategie kennen, da dann Sieger und Verlierer von vornherein feststehen. Tatsächlich steht der Gewinner genau dann von vornherein fest, wenn einer der beiden Spieler die optimale Strategie spielt und an eine C-Stellung gerät.

Da bei einer vorliegenden C-Stellung die Z-Stellungen unter den Nachfolgestellungen eine verschwindende Minderheit darstellen, hat ein perfekter Spieler, der bei einer Z-Stellung beginnen – also seinem Gegenspieler eine C-Stellung überlassen – muss, umso größere Gewinnchancen je größer das Ausgangstableau ist und je mehr „Fehler“möglichkeiten damit für den Gegenspieler bestehen. Und nach dem ersten Fehlgriff von dessen Seite ist er von der Straße des Sieges nicht mehr abzubringen.

Literatur

G.H. Hardy, E. M. Wright: An introduction to the theory of numbers. Fifth edition. The Clarendon Press, Oxford University Press, New York, 1979. p.117-120.

Einzelnachweise

1. ↑ Claude Berge: Graphs et hypergraphes. Dunod, Paris 1970, Chapitre 14 Noyaux et fonctions de Grundy, S. 308.
2. ↑ Claude Berge, a. a. O., S. 290-313: