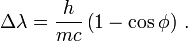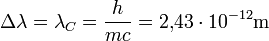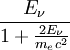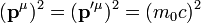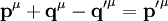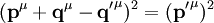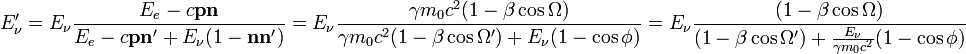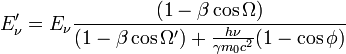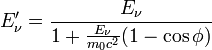Compton-Kante

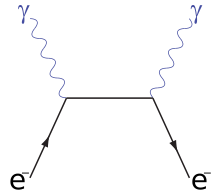
Feynman-Diagramme
s-Kanal
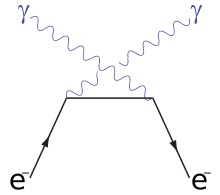
u-Kanal

Als Compton-Effekt bezeichnet man die Vergrößerung der Wellenlänge eines Photons bei der Streuung an einem Elektron oder einem anderen geladenen Teilchen. Dieser Streuprozess ist nach Arthur Compton benannt und heißt Compton-Streuung.

Geschichte

Bis zur Entdeckung des Compton-Effekts war der Photoeffekt der einzige Befund, dass Licht sich nicht nur wie eine Welle, sondern auch, wie von Albert Einstein 1905 postuliert, wie ein Strom von Teilchen verhält (siehe auch Welle-Teilchen-Dualismus).

Als Arthur Compton im Jahre 1922 die Streuung von hochenergetischen Röntgenstrahlen an Graphit untersuchte, machte er zwei Beobachtungen: Zum einen war die Streuwinkelverteilung in Vorwärts- und Rückwärtsrichtung nicht gleich, und zum anderen war die Wellenlänge der gestreuten Strahlung länger als die der einfallenden Strahlung. Beide Beobachtungen waren mit der Vorstellung unverträglich, eine elektromagnetische Welle werde an freien Elektronen (Thomson-Streuung) oder an gebundenen Elektronen (Rayleigh-Streuung) gestreut.

Stattdessen zeigten Comptons Messungen, dass sich die Wellenlänge der gestreuten Strahlung je nach Streuwinkel wie bei einem Stoß von Teilchen, dem Photon und dem Elektron, verhält (Herleitung siehe unten). Damit bewies Compton den Teilchencharakter von Licht oder den Wellencharakter der Elektronen. Behandelt man Elektronen als Materiewellen und Licht als elektromagnetische Welle, so ergibt sich wie in den obigen Feynmangraphen wiederum der Compton-Effekt. ^{[1] [2]}

Compton-Formel

Energien von Elektron und Photon bei der Compton-Streuung eines Photons mit 500 keV

Nach der Streuung an einem freien Elektron hat sich die Wellenlänge des Photons um

$\Delta \lambda=\frac{h}{m c}\left(1- \cos \phi \right)\,.$

vergrößert. Dabei bezeichnet h das plancksche Wirkungsquantum, m die Masse des Elektrons, c die Lichtgeschwindigkeit und φ den Winkel, um den sich die Bewegungsrichtung des Photons durch die Streuung geändert hat. Die Frequenz und die Energie des Photons vermindern sich entsprechend mit der Wellenlänge, wohingegen die Energie des Elektrons um diesen Betrag zunimmt.

Die Wellenlängenänderung des Photons hängt nur vom Streuwinkel φ und nicht etwa von seiner ursprünglichen Wellenlänge ab.

Da der Kosinus bei einer Streuung um 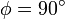$\phi = 90^\circ$ verschwindet, ist

$\Delta \lambda = \lambda_C = \frac{h}{m c}=2{,}43 \cdot 10^{-12}\rm{m}$

Diese Wellenlängenänderung wird als „Compton-Wellenlänge des Elektrons“ bezeichnet und ist wegen ihrer geringen Größe der Grund dafür, dass der Compton-Effekt nur bei solch hochfrequenter Strahlung wie Röntgen- oder Gammastrahlung beobachtet werden kann.

Bei einem Winkel von 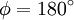$\phi = 180^\circ$ wird der negative Kosinus hingegen maximal, sodass sich die Wellenlänge des Photons höchstens um

Δλ = 2λ_C

vergrößern kann. In diesem Fall wird es in die ursprüngliche Richtung zurückgestreut (Rückstoß).

Compton-Streuung

Compton-Streuung ist der dominierende Wechselwirkungsprozess von Photonen mit Materie für Photonenenergien zwischen etwa 100 keV bis 10 MeV. Der Wirkungsquerschnitt für die Comptonstreuung ist (in der Näherung freier Elektronen) durch die Klein-Nishina-Formel gegeben.

Ist das Elektron an ein Atom gebunden, so gibt die Compton-Formel die Wellenlängenverschiebung nur noch näherungsweise an, da der Impuls des Elektrons in der Atomhülle zufallsverteilt ist. Den Einfluss des Impulses auf die Winkelabhängigkeit der Energie des gestreuten Photons wird als Dopplerverbreiterung bezeichnet. Sie ist bei niedrigen Energien, großen Streuwinkeln und Atomen mit hoher Kernladungszahl besonders stark ausgeprägt.

Bei der Compton-Streuung in Materie wird ein Elektron aus der Atomhülle geschlagen. Somit ist dies ein wichtiger Ionisationsprozess.

Beim inversen Compton-Effekt streut ein hochenergetisches Elektron (oder ein anderes geladenes Teilchen, etwa ein Proton) an einem niederenergetischen Photon und überträgt Energie auf das Photon. Der inverse Compton-Effekt tritt in Teilchenbeschleunigern auf und kann in der Astrophysik bei Ausströmungen in den Koronen von Akkretionsscheiben aktiver Galaxienkerne und bei Supernovae beobachtet werden (siehe auch Sunjajew-Seldowitsch-Effekt). Inverse Compton-Streuung an der Hintergrundstrahlung beschränkt die Maximalenergie von Protonen in der kosmischen Strahlung.

Der Compton-Effekt kann nicht mit der Vorstellung der klassischen Physik erklärt werden, dass Licht eine elektromagnetische Welle sei, die ein geladenes Teilchen in Schwingungen versetzt. Es würde mit der Frequenz der einfallenden Welle schwingen und eine Welle mit unveränderter Frequenz aussenden. In Übereinstimmung mit den Messungen wird die Compton-Streuung als Stoß zweier Teilchen, Photon und Elektron, beschrieben. Dies zeigt, dass Licht Teilcheneigenschaften hat (siehe Welle-Teilchen-Dualismus) oder dass Elektronen Welleneigenschaften haben. Denn wenn man Elektronen durch Materiewellen und Licht durch eine elektromagnetische Welle beschreibt, ergibt sich bei ihrer Wechselwirkung ebenfalls der Compton-Effekt.

Anwendungen

Da es sehr schwierig ist, Gammastrahlung mittels Linsen zu fokussieren, spielt der Compton-Effekt eine wichtige Rolle bei der Abbildung mittels Gammastrahlen im Energiebereich von einigen hundert Kiloelektronenvolt bis zu einigen zehn Megaelektronenvolt. In sogenannten Compton-Teleskopen (auch Compton-Kameras genannt) misst man Energie und Richtung des gestreuten Photons sowie Energie und (manchmal) auch Richtung des Elektrons. So können Energie, Ursprungsrichtung und unter Umständen die Polarisation des einfallenden Photons bestimmt werden. In der Realität wird dies durch Messunsicherheiten und nicht gemessene Größen wie die Richtung des Elektrons jedoch stark erschwert, so dass komplexe Ereignis- und Bildrekonstruktionsmethoden angewandt werden müssen.

Das wohl bekannteste Compton-Teleskop war COMPTEL, das an Bord des NASA-Satelliten CGRO von 1991 bis 2000 als erstes Teleskop den Sternenhimmel im Energiebereich zwischen 0,75 und 30 MeV erforschte. Zu den Erfolgen von COMPTEL zählen u. a. die Erstellung der ersten Himmelskarten in diesem Energiebereich, die Erforschung der Nukleosynthese z. B. von radioaktivem ²⁶Al (massereiche Sterne und Supernovae) und ⁴⁴Ti sowie Fortschritte bei der Erforschung von Pulsaren, Aktiven Galaxien (AGNs) etc.

Es laufen Entwicklungsarbeiten zum Einsatz von Compton-Kameras im Bereich der Medizin oder Nukleartechnik. In der Medizin könnten sie gegenüber den heute verwendeten Szintigraphie-Gammakameras Bilder mit besserer räumlicher Auflösung liefern, also Tumore und Metastasen exakter lokalisieren. In der Nukleartechnik könnten in Zukunft mittels Compton-Kameras z. B. Nuklearanlagen oder nukleare Abfälle überwacht werden.

Im Bereich der Flugsicherung wurden Scanner-Geräte entwickelt, welche die Compton-Rückstreuung (engl. Backscatter) von Röntgenstrahlung an Oberflächen nutzen. Diese werden zur Zeit in den USA getestet.

Compton-Kontinuum und Compton-Kante

Energieverteilung der Compton-Elektronen bei einfallenden monochromatischen γ-Quanten mit der Energie hν

γ-Spektrum einer Am-Be-Quelle, aufgenommen mit einem Germanium-Detektor.

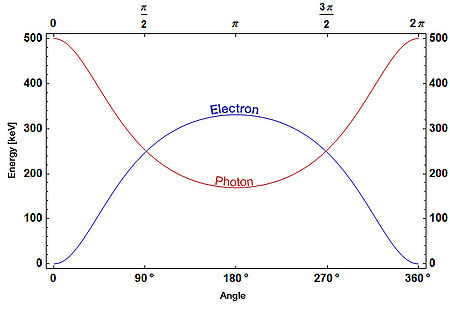
Aus den unten hergeleiteten Formeln errechnet man leicht einen Ausdruck für die Energie des Photons E_ν' und die kinetische Energie des Elektrons E_e' nach der Streuung:

• Photon: $E_{\nu}'(\phi)=\frac{E_{\nu}}{1+\frac{E_{\nu}}{m_ec^2}(1-\cos\phi)}$

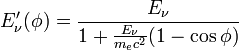
• Elektron: E_e'(φ) = E_ν − E_ν'(φ) $=E_{\nu}\left(1-\frac{1}{1+\frac{E_{\nu}}{m_ec^2}(1-\cos(\phi))}\right)$

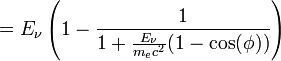
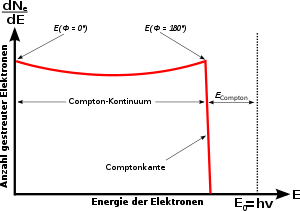
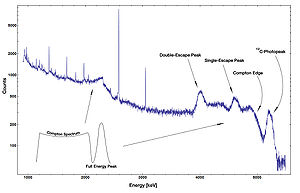
Werden viele Photonen der Energie E_ν = hν nach Compton gestreut (etwa in einem Szintillator), so ergibt sich ein charakteristisches Energiespektrum der gestreuten Elektronen, wie es die nebenstehende Grafik zeigt. Die hierbei auf die Elektronen übertragene Energie ist ob der Abhängigkeit vom Streuwinkel φ kontinuierlich (Compton-Kontinuum), hat jedoch eine scharfe obere Schranke. Diese sogenannte Compton-Kante ergibt sich, weil die gestreuten Photonen bei φ = 180° die größt mögliche Energie an die Elektronen übertragen. Somit liegt die Kante im Spektrum bei

$E_{\rm e}'(180^\circ)=E_{\nu}\left(1-\frac{1}{1+\frac{2 E_{\nu}}{m_ec^2}}\right) = \frac{2 E_{\nu}^2}{m_ec^2+2 E_{\nu}}$.

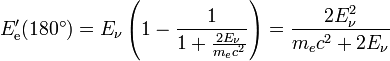Zusätzlich erhält man im Elektronenspektrum einen „Photopeak“ (Spektrallinie) bei der Energie E_ν. In diesem Fall wird die gesamte Energie des Photons auf das Elektron übertragen. Dies geschieht nicht aufgrund des Compton-Effekts, sondern ist das Resultat des Photoeffekts. Aus der obigen Formel lässt sich ablesen, dass sich die zu einem solchen Peak gehörige Compton-Kante um

$\frac{E_{\nu}}{1+\frac{2 E_{\nu}}{m_ec^2}}$

links von diesem Peak befindet.

Die Abbildung rechts zeigt ein mit einem Halbleiterdetektor aufgenommenes γ-Spektrum. Bei etwa 4.4 MeV findet sich der Photopeak von ¹²C, welcher ob relativistischer Geschwindigkeiten der Kohlenstoff-Kerne dopplerverbreitert ist. Da beim Photoeffekt die gesamte Energie des Photons von den Kernen absorbiert wird, entsprechen diese 4.4 MeV der Energie E_ν. Mit der obigen Gleichung folgt daraus, dass die zugehörige Compton-Kante bei etwa 4.2 MeV liegen muss, wo wir sie in der Abbildung auch leicht erkennen.

Weiter links zeigt sich das in der obigen Abbildung skizzierte Kontinuum. Aufgrund eines anderen Effektes, der Paarerzeugung finden sich dort noch zwei weitere Peaks, die allerdings nichts mit dem Compton-Effekt zu tun haben.

Herleitung der Compton-Formel

Bei den unterschiedlichen Herleitungen wird immer ein freies Elektron angenommen. Ist das Elektron in einem Atom gebunden, muss man die Bindungsenergie von der kinetischen Energie des Elektrons nach dem Stoß abziehen.

Ruhendes Elektron

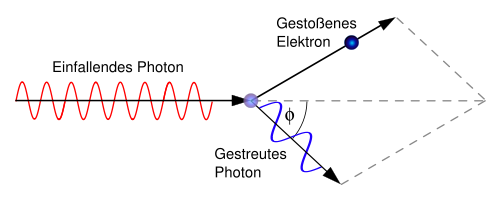
Im Folgenden berechnen wir die Compton-Formel, indem wir das Teilchen als zu Beginn ruhend annehmen. Bei der Streuung überträgt das Photon einen Teil seiner Energie auf das Elektron, sodass sich die beiden Teilchen nach der Streuung in verschiedenen Richtungen auseinander bewegen.

Zunächst betrachten wir, welche Energie und welchen Impuls die jeweiligen Teilchen vor sowie nach der Streueung tragen:

Energie des Elektrons vorher	Energie des Photons vorher	Impuls des Photons vorher	Impuls des Elektrons vorher
Ee = m0c2	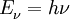$E_\nu^{}=h\nu$	pν = hν / c	pe = 0
Energie des Elektrons nachher	Energie des Photons nachher	Impuls des Photons nachher	Impuls des Elektrons nachher
Ee'	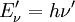$E_\nu^{\prime }=h\nu'$	p'ν = hν' / c	p'e

Die beiden Teilchen müssen vor und nach der Streuung den Energie- und Impulserhaltungssatz erfüllen.

Energieerhaltungssatz	Impulserhaltungssatz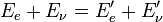
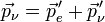
$E_e+E_\nu = E_e'+E_\nu^{\prime}$	$\vec p_\nu=\vec p^{\,\prime}_e+\vec p^{\,\prime}_\nu$

Da wir noch einen Ausdruck für E_e' benötigen, stellen wir den Energieerhaltungssatz danach um und setzen die entsprechenden Größen ein.

E_e' = hν − hν' + m₀c²

In der speziellen Relativitätstheorie stehen die Energie und der Impuls eines Teilchens über die sogenannte Energie-Impuls-Beziehung miteinander in Zusammenhang. Weiterhin benötigen wir den Kosinussatz aus der Trigonometrie, da sich die Teilchen auf den Seiten eines Dreiecks bewegen, die ihrem jeweiligen Impuls entsprechen. Wir benutzen ihn dafür, um den uns unbekannten Impuls des Elektrons p'_e durch den Impuls des Photons p_ν auszudrücken.

Energie-Impuls-Beziehung	Kosinussatz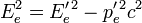
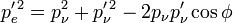
$E_e^2=E_e^{\prime\,2}-p_e^{\prime\,2} c^2$	$p_e^{\prime\,2} = p_\nu^2+p_\nu^{\prime\,2}-2p_\nu p'_\nu \cos \phi$

Nun setzen wir unsere Ausdrücke für E_e' und p'_e in die Energie-Impuls-Beziehung ein, multiplizieren alle Klammern aus und fassen die vielen Terme zusammen

$\left(h\nu-h\nu'+m_0c^2\right)^2-\left(p_\nu^2+p^{\prime 2}_\nu-2p_\nu p'_\nu \cos \phi\right)c^2=m_0^2c^4$

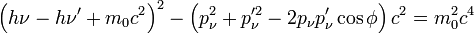
$\left(h\nu-h\nu'+m_0c^2\right)^2-\left[\left(\frac{h\nu}{c}\right)^2+\left(\frac{h\nu'}{c}\right)^2-2\left(\frac{h\nu}{c}\right)\left(\frac{h\nu'}{c}\right) \cos \phi\right]c^2=m_0^2c^4$

$\left(h\nu\right)^2-h^2\nu\nu'+h\nu m_0c^2-h^2\nu\nu'+\left(h\nu'\right)^2-h\nu'm_0c^2+h\nu m_0c^2-h\nu 'm_0c^2+\left(m_0c^2\right)^2$ $-\left(h\nu\right)^2-\left(h\nu'\right)^2+2h^2\nu\nu' \cos \phi = m_0^2c^4$

$\left(h\nu\right)^2-2h^2\nu\nu'+2h\nu m_0c^2+\left(h\nu' \right)^2-2h\nu'm_0c^2-\left(h\nu \right)^2-\left(h\nu'\right)^2+2h^2\nu\nu' \cos \phi=0$

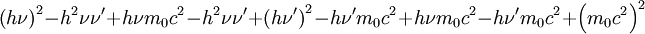
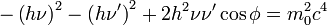
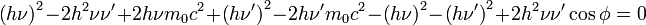
2hνm₀c² − 2hν'm₀c² − 2h²νν' + 2h²νν'cosφ = 0

$2h\nu m_0c^2-2h\nu'm_0c^2-2h^2\nu\nu'\left(1- \cos \phi \right)=0$

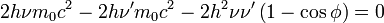
$2h\left[m_0c^2\left(\nu-\nu'\right)\right]=2h^2\nu\nu'\left(1- \cos \phi \right)$

$m_0c^2\left(\nu-\nu'\right)=h\nu\nu'\left(1- \cos \phi \right)$

$\frac{\nu-\nu'}{\nu\nu'}=\frac{h}{m_0c^2}\left(1- \cos \phi \right)$

$\frac{1}{\nu'}-\frac{1}{\nu}=\frac{h}{m_0c^2}\left(1- \cos \phi \right)$

$\frac{c}{\nu'}-\frac{c}{\nu}=\lambda'-\lambda=\frac{h}{m_0c}\left(1- \cos \phi \right)$

$\Delta \lambda=\frac{h}{m_0c}\left(1- \cos \phi \right)$

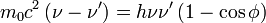
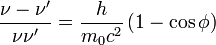
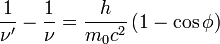
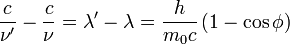
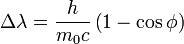
Im letzten Schritt haben wir verwendet, dass die Wellenlänge und die Frequenz über c = λν miteinander zusammenhängen (Wellengleichung).

Beliebiges Bezugssystem

Während sich der Compton-Effekt im Falle eines ruhenden Elektrons leicht triogonometrisch berechnen lässt, stellt sich die Situation schwieriger dar, wenn wir sie aus einem beliebigen Bezugssystem betrachten. In diesem Fall bewegt sich das Elektron vor dem Stoß mit der Geschwindigkeit v, wobei es die Gesamtenergie E_e = γm₀c² und den Impuls 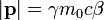$|\mathbf p|=\gamma m_{0}c\mathbf{\beta}$ trägt,

mit 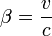$\beta=\frac{v}{c}$ und $\gamma=\frac{1}{\sqrt{1-\beta^2}}$.

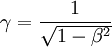Um den Compton-Effekt im nun betrachteten Fall zu berechnen, verwenden wir den Vierervektor-Formalismus.

Die Viererimpulse, welche die beteiligten Teilchen vor und nach dem Streuprozess besitzen, sind

Elektron vorher	Photon vorher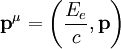
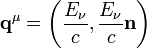
$\mathbf{p}^{\mu}= \left(\frac{E_{e}}{c}, \mathbf {p}\right)$	$\mathbf{q}^{\mu} = \left(\frac{E_\nu}{c}, \frac{E_\nu}{c}\mathbf {n}\right)$
Elektron nachher	Photon nachher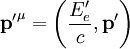
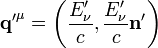
$\mathbf{p'}^{\mu} = \left(\frac{E'_{e}}{c}, \mathbf {p}'\right)$	$\mathbf{q'}^{\mu} = \left(\frac{E'_\nu}{c}, \frac{E'_\nu}{c}\mathbf {n}'\right)$

Hierbei bezeichnet 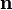$\mathbf{n}$ einen Einheitsvektor, der in Bewegungsrichtung des Photons zeigt.

Da wir die Produkte von jeweils zwei der einzelnen Impulse benötigen werden, wollen wir diese nun berechnen. Für die Quadrate gilt stets

$(\mathbf{p}^{\mu})^2 = (\mathbf{p'^{\mu}})^2 = (m_{0}c)^2$

$(\mathbf{q}^{\mu})^2 = (\mathbf{q'}^{\mu})^2 = \frac{E^2_\nu}{c^2}- \frac{E^2_\nu}{c^2}\mathbf{n}^2 = 0$,

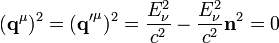wobei zu beachten ist, dass 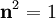$\mathbf n^2 = 1$ gilt, da es sich bei 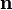$\mathbf{n}$ um einen Vektor mit der Länge 1 handelt.

Nun fehlen uns noch die gemischten Produkte:

$\mathbf{p}_{\mu} \mathbf{q}^{\mu} = E_\nu\left(\frac{E_e}{c^2} - \frac{1}{c} \mathbf p \mathbf n\right) = E_\nu\left(\frac{\gamma m_{0}c^2}{c^2} - \frac{1}{c}|\mathbf p| |\mathbf n| \cos \Omega\right) = E_\nu\left(\frac{\gamma m_{0}c^2}{c^2} - \frac{1}{c}\gamma m_{0}c \beta \cos \Omega\right) = \gamma m_{0}E_\nu (1- \beta \cos \Omega)$.

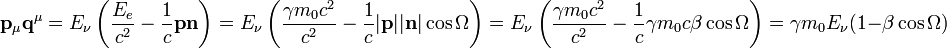Bei Ω handelt es sich um den Winkel zwischen Elektron und Photon vor der Streuung.

Analog erhält man

$\mathbf{p}_{\mu} \mathbf{q'}^{\mu} = E'_\nu\left(\frac{E_e}{c^2} - \frac{1}{c} \mathbf p \mathbf n'\right) = \gamma m_{0}E'_\nu (1- \beta \cos \Omega')$,

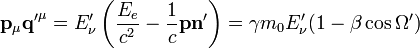wobei Ω' der Winkel zwischen dem Elektron vor der Streuung und dem Photon nach der Streuung ist.

$\mathbf q_{\mu} \mathbf q'^{\mu} = \frac{E_\nu E'_\nu}{c^2}(1-\mathbf n \mathbf n') = \frac{E_\nu E'_\nu}{c^2}(1-\cos\phi)$,

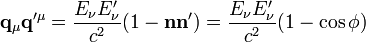wobei φ der Winkel zwischen dem Photon vor der Streuung und dem Photon nach der Streuung ist.

Wird ein Photon an einem Elektron gestreut, so muss die Energie- und Impulserhaltung erfüllt sein. Da die Energie die Nullkomponente des Vierimpulses ist und die restlichen Komponenten den Impuls repräsentieren, folgt

$\mathbf{p}^{\mu} + \mathbf{q}^{\mu} -\mathbf{q'}^{\mu} = \mathbf{p'}^{\mu}$

$(\mathbf{p}^{\mu} + \mathbf{q}^{\mu} -\mathbf{q'}^{\mu})^2 = (\mathbf{p'}^{\mu})^2$

$(\mathbf p^{\mu})^2 + 2 \mathbf p_{\mu} \mathbf q^{\mu} - 2 \mathbf{q}_{\mu} \mathbf{q'}^{\mu} - 2 \mathbf{p}_{\mu} \mathbf{q'}^{\mu} + (\mathbf{q}^{\mu})^2 +(\mathbf{q'}^{\mu})^2 = (\mathbf{p'}^{\mu})^2$.

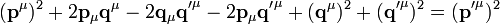Unter Verwendung von 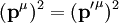$(\mathbf{p}^{\mu})^2 = (\mathbf{p'}^{\mu})^2$, sowie 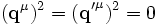$(\mathbf{q}^{\mu})^2 = (\mathbf{q'}^{\mu})^2 = 0$ vereinfacht sich dies zu

$\mathbf{p}_{\mu} \mathbf{q}^{\mu} - \mathbf{q}_{\mu} \mathbf{q'}^{\mu} - \mathbf{p}_{\mu} \mathbf{q'}^{\mu} = 0$.

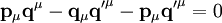Nach Einsetzen der zuvor berechneten Komponenten erhalten wir

$E'_\nu = E_\nu \frac{E_e - c\mathbf p \mathbf n}{E_e - c\mathbf p \mathbf n'+E_\nu(1-\mathbf n\mathbf n')}= E_\nu \frac{\gamma m_{0}c^2(1-\beta\cos\Omega)}{\gamma m_{0}c^2(1-\beta\cos\Omega')+E_\nu(1-\cos\phi)}= E_\nu \frac{(1-\beta\cos\Omega)}{(1-\beta\cos\Omega')+\frac{E_\nu}{\gamma m_{0}c^2}(1-\cos\phi)}$

$E'_\nu = E_\nu \frac{(1-\beta\cos\Omega)}{(1-\beta\cos\Omega')+\frac{h\nu}{\gamma m_{0}c^2}(1-\cos\phi)}$

Je nach Einfallswinkel und kinetischer Energie kann das Elektron eine gewisse Energie an das Photon übertragen (inverse Compton-Streuung). Im Ruhesystem des Elektrons war die Geschwindigkeit desselben vor dem Stoß gleich Null. Demnach ist

γ = 1 und β = 0,

womit sich die bereits bekannte Formel

$E'_\nu = \frac{E_\nu}{1+ \frac {E_\nu}{m_{0} c^2}(1-\cos\phi)}$

ergibt.

Einzelnachweise

1. ↑ Arthur H. Compton: . In: Bull. Nat. Research Council. 20, 1922, S. 10. 
2. ↑ Arthur H. Compton: A Quantum Theory of the Scattering of X-rays by Light Elements. In: Physical Review. 21, Nr. 5, 1923, S. 483-502 (doi:10.1103/PhysRev.21.483). 

Weblinks

• Verschiedene Versuche und Animationen (bei Leifiphysik)
• Animation zur Richtungsverteilung von Photon und Elektron (bei BIGS)