Erdschwerefeld

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Das Erdschwerefeld ist das Kraftfeld der Schwerebeschleunigung (anders gesagt: der Schwerefeldstärke) im Einflussbereich der Erde. Es wird verursacht und beeinflusst durch:

1. die Gravitationswirkung der Erdmasse,
2. die aus der Erdrotation resultierende Zentrifugalkraft (Fliehkraft),
3. Unregelmäßigkeiten im Aufbau und in der Form der Erde

und gestört durch die Gezeiten, d. h. die Gravitationswirkung von Mond und Sonne.

Den weitaus größten Einfluss auf das Schwerefeld der Erde hat die Gravitation der Erdmasse sowie die Höhe bzw. der Abstand vom Erdmittelpunkt. Die anderen Faktoren führen nur zu kleinen Abweichungen.

Zonen

Da die Erde annähernd Kugelgestalt hat, ist das Vektorfeld der Gravitation, von kleinen Schwankungen abgesehen, kugelsymmetrisch. Die Richtung seiner Vektoren ist überall im Raum annähernd auf den Erdmittelpunkt ausgerichtet. Die Feldstärke hängt vor allem von der Entfernung vom Erdmittelpunkt ab. Im Folgenden werden drei Zonen unterschieden:

Erdoberfläche

Schwerefeld der Erde im Südpolarmeer

An der Erdoberfläche hat die Schwerebeschleunigung einen Betrag von etwa 9,81 m/s². Sie ist dort jedoch nicht einheitlich, da die Erde keine exakte Kugelform hat (siehe Geoid) und außerdem rotiert, so dass die Schwerkraft am Äquator durch die Fliehkraft etwas abgeschwächt wird. An den Erdpolen entfällt der Einfluss der Fliehkraft dagegen.

Durch die Summe beider Effekte ist auf der Erdoberfläche die Anziehung am Pol um ca. 0,5 % größer als am Äquator. Die Schwerebeschleunigung beträgt 9,832 m/s² an den Polen und 9,745 m/s² am Äquator. Man spricht hier auch von der Schwereabplattung der Erde. Ein Mensch, der am Äquator ein Gewicht von 800 N hat, wiegt an den Erdpolen 804,24 N. Mit einer Normalschwereformel kann die Schwerebeschleunigung an einem Punkt auf der Erdoberfläche abgeschätzt werden.

Weiterhin weist das Schwerefeld kleinere Schwereanomalien auf, d. h. globale, regionale und lokale Unregelmäßigkeiten, da die Masse sowohl in der Erdkruste (Gebirge, Kontinentalplatten) als auch tiefer (in Erdmantel und -Kern) nicht gleichmäßig verteilt ist. Diese zusätzlichen Abweichungen wirken sich auf den Betrag der Schwerkraft mit bis zu 0,01 % aus, und auch die Lotrichtung wird um bis zu 0,01° von der Richtung zum Erdmittelpunkt abgelenkt (Lotabweichung). Als Folge davon weicht das Geoid - das heute vorwiegend durch Satellitengeodäsie bestimmt wird - vertikal bis zu 100 m vom mittleren Erdellipsoid ab.

Mit den Schwankungen der Schwerkraft auf der Erdoberfläche befassen sich die Artikel Schweregradient und Vertikalgradient genauer.

Im Erdinneren

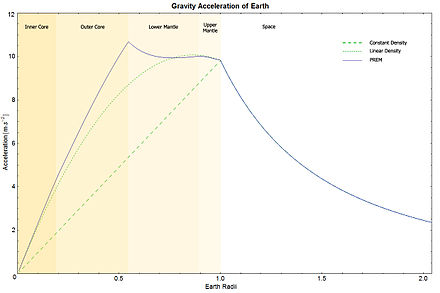Gravitation im Erdinnern nach dem seismischen PREM-Erdmodell, sowie Näherungen durch konstante und linear nach innen zunehmende Gesteinsdichte.

Am Erdmittelpunkt wirkt keine Schwerkraft, es herrscht Schwerelosigkeit. Im Erdkern wächst die Schwerebeschleunigung mit dem Abstand vom Erdmittelpunkt monoton an. An der Wiechert-Gutenberg-Diskontinuität, der Grenze von Erdkern und Erdmantel (bei ca. 3480 km Entfernung vom Erdmittelpunkt, oder anders gesagt in ca. 2900 km Tiefe), erreicht sie ein Maximum von knapp 10,68 m/s². Dieser Effekt hat seine Ursache darin, dass der überwiegend metallische Erdkern mehr als doppelt so dicht wie der Erdmantel und die Erdkruste ist. Von dort bis zu ca. 4900 km nimmt sie zunächst wieder langsam bis auf 9,93 m/s² ab, steigt nochmals bei 5700 km auf 10,01 m/s² und sinkt dann monoton bis sie an der Erdoberfläche etwa 9,82 m/s² erreicht.

Im Physik-Schulunterricht wird oft die Aufgabe gestellt, zu berechnen, wie der Schwerkraftverlauf im Erdinneren unter der Annahme wäre, dass die Erde eine homogene Kugel sei. Unter dieser Annahme ergäbe sich ein linearer Anstieg der Schwerebeschleunigung von null am Erdmittelpunkt bis zu einem Maximum an der Erdoberfläche; ab diesem Punkt folgt die Kurve dann dem invers-quadratischen Verlauf.

Ebenfalls bekannt ist das folgende Gedankenexperiment im Zusammenhang mit dem Erdschwerefeld im Erdinneren: Könnte man einen Tunnel durch die Erde hindurch bohren, Reibungsverluste ausschalten und dem Einfluss der Corioliskraft entgegenwirken und wäre die Dichte der Erde in jedem Punkt gleich der mittleren Dichte der Erde, würde ein in diesen Schacht hineinfallender Gegenstand im freien Fall in rund 42 Minuten bis zum anderen Ende hindurchfallen. Die Bewegung des Gegenstandes wäre wie eine Schwingung mit einer Periodenlänge von 84 Minuten, der sogenannten Schuler-Periode.

Außerhalb der Erde

Außerhalb der Erde nimmt die Schwerebeschleunigung proportional zum Quadrat des Abstandes vom Erdmittelpunkt ab. Das Erdschwerefeld ist somit (wie das Schwerefeld jedes Himmelskörpers) prinzipiell unbegrenzt, wird aber mit wachsender Entfernung schnell schwächer.

Im Weltraum überlagern sich die Schwerefelder sämtlicher Himmelskörper. Auf der Strecke zwischen Erde und Mond heben sich an einem bestimmten Punkt das Schwerefeld der Erde und das des Mondes gegenseitig auf. Etwas näher zur Erde befindet sich ein Punkt, an dem die Schwerefelder auch die Zentripetalkraft aufheben, dieser ist der Lagrange-Punkt L₁ des Systems Erde-Mond. Geht man über diesen Punkt in Richtung des Mondes hinaus, überwiegt die Anziehungskraft des Mondes.

Nur im Nahbereich eines schweren Himmelskörpers kann der Einfluss der anderen Himmelskörper in der Praxis vernachlässigt werden, da er dann sehr gering ist – der Einfluss des nahen Körpers ist dominierend.

Im näheren Weltraum um die Erde herum (z. B. im Bereich der Umlaufbahnen der künstlichen Erdsatelliten) ist das Schwerefeld wegen der genannten Schwereanomalien nur annähernd kugelförmig. Die Abweichungen in Betrag und Richtung liegen im Promillebereich und beeinflussen erdnahe Satellitenbahnen auf einige Kilometer bzw. Zehntelgrad.

Siehe auch

• Geopotential (das Schwerepotential der Erde)
• Fluchtgeschwindigkeit aus dem Schwerefeld

Literatur

• Christoph Reigber, Peter Schwintzer: Das Schwerefeld der Erde. In: Physik in unserer Zeit. 34 (5), 2003, S. 206–212, ISSN 0031-9252

Weblinks

• GeoForschungsZentrum Potsdam: Gravity Field and Gravimetry