Euklid von Alexandria

Fantasieporträt der frühen Neuzeit

Euklid von Alexandria (griechisch Εὐκλείδης Eukleidēs; latinisiert Euclides; ca. 360 v. Chr. bis ca. 280 v. Chr.) war ein griechischer Mathematiker.

Die überlieferten Werke umfassen sämtliche Bereiche der antiken, griechischen Mathematik: das sind die theoretischen Disziplinen Arithmetik und Geometrie (Die Elemente, Data), Musiktheorie (Die Teilung des Kanon), eine methodische Anleitung zur Findung von planimetrischen Problemlösungen von bestimmten gesicherten Ausgangspunkten aus (Porismen) sowie die physikalischen bzw. angewandten Werke (Optik, astronomische Phänomene).

In seinem berühmtesten Werk Die Elemente (griechisch Στοιχεῖα Stoicheia; vermutlich um 325 v. Chr. entstanden) trug er das Wissen der griechischen Mathematik seiner Zeit zusammen. Er zeigte darin die Konstruktion geometrischer Objekte, natürlicher Zahlen sowie bestimmter Größen und untersuchte deren Eigenschaften. Dazu benutzte er Definitionen, Postulate (nach Aristoteles Grundsätze, die akzeptiert oder abgelehnt werden können) und Axiome (nach Aristoteles allgemeine und unbezweifelbare Grundsätze). Viele Sätze der Elemente stammen offenbar nicht von Euklid selbst, seine Hauptleistung besteht in der Sammlung und einheitlichen Darstellung des mathematischen Wissens sowie der strengen Beweisführung, die zum Vorbild für die spätere Mathematik wurde.

Leben

Über das Leben des griechischen Mathematikers Euklid ist wenig bekannt. Man nimmt an, dass er um das Jahr 360 v. Chr. vermutlich in Athen geboren wurde und dass er seine Ausbildung an Platons Akademie in Athen erhielt. Man ist ziemlich sicher, dass er während der Regierungszeit von Ptolemaios I. (möglicherweise auch noch während der von Ptolemaios II.) in Alexandria gelebt und dort Mathematik gelehrt hat. Berühmt wurde Euklid durch 13 Lehrbücher, in denen das damalige Wissen zur Mathematik zusammengefasst ist. Die Elemente, wie diese Bücher genannt werden, sind die erfolgreichsten Mathematikbücher aller Zeiten. So wurden Übersetzungen dieser Bücher z. B. in England noch im 19. Jahrhundert als offizielle Schulbücher für die Geometrie benutzt.

Über Euklid erzählt man sich viele Anekdoten: Ein Schüler fragte, als er den ersten Satz gelernt hatte: "Was kann ich verdienen, wenn ich diese Dinge lerne?" Da rief Euklid seinen Sklaven und sagte: "Gib ihm drei Obolen, denn der arme Mann muss Geld verdienen mit dem, was er lernt."

Pharao Ptolemaios fragte einmal Euklid, ob es nicht für die Geometrie einen kürzeren Weg gebe, als die Lehre der Elemente. Er aber besaß den Mut zu antworten, dass es zur Geometrie keinen Königsweg gebe. Auch ein König muss sich wie jeder andere Mensch "auf den Hosenboden setzen", wenn er die Mathematik verstehen will.

Geometrie – Arithmetik – Proportionslehre

Die Elemente waren vielerorts bis ins 20. Jahrhundert hinein Grundlage des Geometrieunterrichts, vor allem im angelsächsischen Raum.

Neben der pythagoreischen Geometrie enthalten Euklids Elemente auch in Buch VII-IX die pythagoreische Arithmetik, die Anfänge der Zahlentheorie, die bereits Archytas kannte, darin die Konzepte der Teilbarkeit und des größten gemeinsamen Teilers, sowie auch einen Algorithmus, um ihn zu bestimmen, genannt Euklidischer Algorithmus. Euklid bewies auch, dass es unendlich viele Primzahlen gibt. Auch Euklids Musiktheorie baut auf der Arithmetik auf. Ferner enthält das Buch V die Proportionslehre des Eudoxos, eine Verallgemeinerung der Arithmetik auf positive irrationale Größen.

Das bekannte fünfte Postulat der ebenen Euklidischen Geometrie, heute Parallelenaxiom genannt, fordert, dass wenn eine Strecke s beim Schnitt mit zwei Geraden g und h bewirkt, dass die innen auf derselben Seite von s entstehenden Winkel α und β zusammen kleiner als zwei rechte Winkel werden, dann treffen sich die beiden Geraden g und h auf der Seite von s, auf der die Winkel α und β liegen. Schneiden also zwei Geraden eine Strecke (oder Gerade), so dass die auf einer Seite von der Strecke und den zwei Geraden eingeschlossenen zwei Winkel kleiner als 180° sind, dann schneiden sich die beiden Geraden auf dieser Seite und begrenzen zusammen mit der Strecke (oder dritten Geraden) ein Dreieck.

Für die Wissenschaftsgeschichte ist die Beschäftigung mit dem Parallelenaxiom von großer Bedeutung, weil sie viel zur Präzisierung mathematischer Begriffe und Beweisverfahren beigetragen hat. Im Zuge dessen wurden im 19. Jahrhundert auch die Unzulänglichkeit der Euklidischen Axiome offenkundig. Eine formale Axiomatik der Euklidischen Geometrie findet sich in David Hilberts Werk „Grundlagen der Geometrie“ (1899), das zu vielen weiteren Auflagen und anschließenden Forschungen geführt hat. Darin wird zum ersten Mal ein vollständiger Aufbau der euklidischen Geometrie geleistet, bis zu der Erkenntnis, dass jedes Modell des Hilbertschen Axiomensystems isomorph zum dreidimensionalen reellen Zahlenraum mit den üblichen Deutungen der geometrischen Grundbegriffe (wie Punkt, Gerade, Ebene, Länge, Winkel, Kongruenz, Ähnlichkeit usw.) in der Analytischen Geometrie ist. Schon seit der Antike versuchten viele bedeutende Mathematiker vergeblich, das Parallelenaxiom mit den übrigen Axiomen und Postulaten zu beweisen (es wäre dann entbehrlich). Erst im 19. Jahrhundert wurde die Verzichtbarkeit des Parallelenaxioms mit der Entdeckung der Nichteuklidischen Geometrie durch Bolyai und Lobatschewski klar. Die Poincaré'sche Halbebene H (Henri Poincaré) ist ein Modell für ein solches Axiomensystem, in dem Parallelen-Axiom nicht gilt, somit kann das Parellenaxiom nicht aus den übrigen Axiomen gefolgert werden. (Siehe Nichteuklidische Geometrie)

Musiktheorie

In Euklids musiktheoretischer Schrift Die Teilung des Kanon (griech. Katatomē kanonos, lat. Sectio canonis) die als authentisch einzustufen ist, griff er die Musiktheorie des Archytas auf und stellte sie auf eine solidere akustische Basis, nämlich auf Frequenzen von Schwingungen (er sprach von Häufigkeit der Bewegungen). Er verallgemeinerte dabei den Satz des Archytas über die Irrationalität der Quadratwurzel 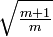$\sqrt{\tfrac{m+1}{m}}$ und bewies ganz allgemein die Irrationalität beliebiger Wurzeln $\sqrt[n]{\tfrac{m+1}{m}}$. Der Grund für diese geniale Verallgemeinerung ist seine Antithese gegen die Harmonik des Aristoxenos, die auf rationalen Vielfachen des Tons (Halbton ... n-tel-Ton) aufbaut. Denn in der pythagoreischen Harmonik hat der Ton (Ganzton) die Proportion 9:8, was Euklid zu seiner Antithese „Der Ton ist weder in zwei noch in mehrere gleiche Teile teilbar“ veranlasste; sie setzt allerdings kommensurable Frequenzen voraus, die in der pythagoreischen Harmonik bis zum Ende des 16. Jahrhunderts (Simon Stevin) angenommen wurden. Die Antithese „Die Oktave ist kleiner als 6 Ganztöne“ stützte er auf die Berechnung des pythagoreischen Kommas. Ferner enthält Euklids Teilung des Kanons – wie ihr Titel signalisiert – die älteste überlieferte Darstellung eines Tonsystems am Kanon, einer geteilten Saite, und zwar eine pythagoreische Umdeutung des vollständigen diationischen Tonsystems des Aristoxenos, das die Harmonie des Philolaos erweitert. Euklids Tonsystem wurde zur Grundlage des modernen Tonsystems mit der heute üblichen Bezeichnung durch die Tonbuchstaben Odos.

Werke (Auswahl)

• Euklid: Die Elemente. Bücher I-XIII. Hrsg. u. übers. v. Clemens Thaer. 4. Aufl., Harri Deutsch, Frankfurt a.M. 2003. (Ostwalds Klass. d. exakten Wiss. 235.) ISBN 3-8171-3413-4
• Euklides: Data. Die Data von Euklid, nach Menges Text aus d. Griech. übers. u. hrsg. v. Clemens Thaer. Springer, Berlin 1962
• Euklid: Teilung des Kanons (sectio canonis), ed. H. Menge in: Euclidis opera omnia, Band 8, Leipzig 1916, 158-183
• Euklid: Sectio canonis, neu ediert, übersetzt und kommentiert in: Busch, Oliver: Logos syntheseos : die euklidische Sectio canonis, Aristoxenos, und die Rolle der Mathematik in der antiken Musiktheorie, Hildesheim, 2004, ISBN/ISSN: 3-487-11545-X

Weitere erhaltene Schriften sind: Optika, Über die Teilung der Figuren (auszugsweise erhalten in einer arabischen Übersetzung). Von weiteren Werken sind nur die Titel bekannt: u.a. Pseudaria (Trugschlüsse), Katoptrika und Phainomena (Astronomie).

Siehe auch

• Euklids Elemente
• Euklids Beweis der Irrationalität der Wurzel aus 2

Literatur

• Wilfried Neumaier: Was ist ein Tonsystem?, Frankfurt am Main, Bern, New York, 1986, Kap. 6, Die „Teilung des Kanons“ des Eukleides.
• Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie. Geschichte, Kulturen, Menschen, Springer, Berlin 2005, ISBN 3-540-22471-8 (S.49-65) – Die Elemente Euklids und andere Schriften sowie im weiteren Verlauf des Buches deren Kontext und Rezeption in der weiteren Entwicklung der Geometrie.
• Max Steck: Bibliographia Euclideana. Die Geisteslinien der Tradition in den Editionen der „Elemente“ des Euklid (um 365-300). Handschriften, Inkunabeln, Frühdrucke (16.Jahrhundert). Textkritische Editionen des 17.-20. Jahrhunderts. Editionen der Opera minora (16.-20.Jahrhundert). Nachdruck, herausgeg. von Menso Folkerts. Hildesheim: Gerstenberg, 1981.
• Bartel Leendert van der Waerden: Geometry and Algebra in Ancient Civilizations. Springer, Berlin 1983, ISBN 3-540-12159-5.

Weblinks

• http://www.anderegg-web.ch/phil/euklid.htm

• Literatur von und über Euklid im Katalog der Deutschen Nationalbibliothek (Datensatz zu Euklid • PICA-Datensatz • Einträge im Musikarchiv)
• Euklids Elemente, alle 13 Bücher in englischer Sprache.
• Euklids Elemente, alle 13 Bücher in griechischer Sprache mit der lateinischer Übersetzung des Heiberg. (PDF)
• Die sechs ersten Bücher Evclidis, Deß Hochgelaehrten weitberuembten, Griechischen Philosophi und Mathematici: von den anfaengen vnd fundamenten der Geometriae. Amsterdam 1618, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden
• Euclidis Megarensis ... sex libri priores, de Geometricis principiis. Basileae 1550, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden
• Euclidis Megarensis Mathematici Clarissimi Elementorum geometricorum Lib. XV. Basileae 1537, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden
• Elementale Geometricum. Argentorati 1529, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden
• Elementorum Libri XV. Coloniae 1627, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden

Personendaten
NAME	Euklid von Alexandria
KURZBESCHREIBUNG	griechischer Mathematiker
GEBURTSDATUM	um 365 v. Chr.
STERBEDATUM	um 300 v. Chr.