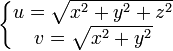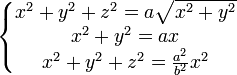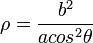- Archytas
-
Archytas von Tarent (* wohl zwischen 435 und 410 v. Chr.; † wohl zwischen 355 und 350 v. Chr.)[1] war ein antiker griechischer Philosoph (Pythagoreer), Mathematiker, Musiktheoretiker, Physiker, Ingenieur, Staatsmann und Feldherr. Er wirkte in seiner Heimatstadt, der griechischen Kolonie Tarent in Apulien (Süditalien).
Inhaltsverzeichnis
Leben
Sein Vater hieß wahrscheinlich Hestiaios.[2] Ansonsten ist über seine Herkunft nichts bekannt. Cicero berichtet, der Lehrer des Archytas sei Philolaos von Kroton gewesen. Das ist plausibel, aber nicht sicher. Philolaos gehörte ebenso wie Archytas der von Pythagoras von Samos gegründeten Schule der Pythagoreer an. Von den Schülern des Archytas ist nur der Mathematiker Eudoxos von Knidos namentlich bekannt.[3]
Tarent hatte damals eine demokratische Verfassung, stand aber im Peloponnesischen Krieg auf der Seite seiner Mutterstadt Sparta, die mit Syrakus verbündet war, gegen das ebenfalls demokratische Athen. Nach dem Ende des Krieges (404) nahm Tarent weiterhin eine freundliche Haltung gegen Syrakus ein und hielt sich aus den militärischen Auseinandersetzungen zwischen dem Tyrannen Dionysios I. von Syrakus und einer 393 gebildeten Liga süditalienischer Griechenstädte heraus. Nachdem der Tyrann 379/378 die führende Stadt der Liga, Kroton, erobert hatte, übernahm Tarent die Führung der Liga, wohl im Einvernehmen mit Dionysios, und entwickelte sich zur Führungsmacht im festländischen Teil der Magna Graecia. Nun begann eine Blütezeit der Stadt, während die Macht von Syrakus nach Dionysios’ Tod (367) abnahm.
Der gut informierte Philosoph Aristoxenos berichtet, dass damals Archytas als einziger siebenmal – gemeint: siebenmal hintereinander – von seinen Mitbürgern zum Feldherrn (Strategen) gewählt wurde, obwohl das Gesetz eigentlich keine unmittelbare Wiederwahl zuließ. Dieser Umstand illustriert das außerordentliche Vertrauen, dessen er sich erfreute. Als führender Staatsmann und Feldherr Tarents war er zugleich Oberkommandierender der Streitkräfte der Liga. Seine Feldzüge, die alle erfolgreich waren, richteten sich gegen die traditionellen Gegner der Griechen, die einheimischen Stämme der Region (Italiker).[4]
Zur Bekanntheit des Archytas in späterer Zeit trug vor allem seine Beziehung zu Platon bei, den er bei dessen erster Italienreise (388/387 v. Chr.) kennenlernte, als Platon Dionysios I. in Syrakus aufsuchte. Archytas wurde Platons Gastfreund (xénos). Platon war wohl in erster Linie an Archytas’ Mathematikkenntnissen interessiert. Dieses Gastfreundschaftsverhältnis beinhaltete gegenseitige Verpflichtungen zu beiderseitigem Vorteil, war aber nicht notwendigerweise mit einer engen persönlichen Freundschaftsbeziehung verbunden. Als Platon im Jahr 361 beim Tyrannen Dionysios II. von Syrakus, dem Sohn Dionysios’ I., in Ungnade gefallen war und mit dem Tod bedroht wurde, hat ihm Archytas einem Bericht des Diogenes Laertios zufolge das Leben gerettet. Dass Archytas, als Platon ihn um Hilfe bat, intervenierte und dem bedrängten Philosophen die Abreise ermöglichte, geht aus Platons siebentem Brief hervor. Eine späte Legende, wonach Platon, der auf Befehl des Tyrannen (Dionysios I.) versklavt worden war, von Archytas gekauft wurde, ist unglaubwürdig.[5]
Früher glaubte man, aus der Ode I 28 des römischen Dichters Horaz schließen zu können, Archytas sei bei einem Schiffbruch in der Adria ums Leben gekommen. Diese Deutung beruht auf einem Missverständnis. Archytas wird zwar in dem Gedicht, das von einem ertrunkenen Seemann handelt, erwähnt, ist aber nicht selbst der Tote.[6]
Werke
Von den echten Werken des Archytas sind nur vier Fragmente erhalten. In den älteren Quellen findet sich keine Werkliste. In späterer Zeit waren viele unechte Werke unter seinem Namen im Umlauf.[7] Die ursprünglichen Titel der echten Werke sind nicht bekannt; sicher ist nur, dass sie seine Hauptthemen Musik (Harmonik) und Mathematik behandelten. Vielleicht verfasste er auch Schriften über Kosmologie und Biologie.[8]
Philosophie
Obwohl Archytas ein jüngerer Zeitgenosse von Sokrates war, wird er zu den Vorsokratikern gezählt, weil er zu einer älteren Tradition gehörte, die noch nicht unter dem Einfluss der sokratischen Philosophie stand.
Archytas betrachtete die Arithmetik, die er „Logistik“ (logistikē) nannte, als Grundlage der Wissenschaften und betonte auch ihren Vorrang vor der Geometrie. In der Hochschätzung der Mathematik stimmte er mit Platon überein. Während jedoch Platon in der Mathematik nur eine Vorbereitung zu einer Philosophie sah, die sich mit rein geistigen Objekten befasst, teilte Archytas Platons Geringschätzung der Empirik nicht und machte auch die scharfe platonische Trennung zwischen den Bereichen des geistig Erkennbaren und des sinnlich Wahrnehmbaren nicht mit. Für ihn als Politiker war die Arithmetik auch deswegen wichtig, weil sie aus seiner Sicht die Möglichkeit bot, einleuchtende Formeln für eine einvernehmliche, ausgewogene Besitzverteilung unter den Bürgern zu finden. Da die Anwendung solcher Formeln für jeden überprüfbar war, konnte damit nach Archytas’ Überzeugung der soziale Frieden hergestellt und bewahrt werden. Dies war in den oft von blutigen Machtkämpfen erschütterten griechischen Städten von größter Bedeutung.[9]
Kosmologie
Die Überlieferung, wonach Archytas sich auf dem Gebiet der Astronomie betätigte, geht auf die römischen Dichter Horaz und Properz zurück, die wohl keine zuverlässigen Informationen darüber besaßen. Authentisch und berühmt ist jedoch seine Argumentation für die Unendlichkeit des Universums. Sie besagt, dass jemand, der an einem angenommenen Ende des Universums angekommen wäre und dort seine Hand oder einen Stab ausstrecken würde, entweder auf einen Körper oder auf leeren Raum stoßen müsste, also auf jeden Fall auf eine Fortsetzung des Universums; daher kann dieses kein Ende haben. Dieser Gedanke wurde von den Stoikern und Epikureern und noch von John Locke und Isaac Newton aufgegriffen und abgewandelt.[10]
Mathematik
Archytas konnte beweisen, dass es irrationale Größenverhaltnisse gibt, die sich nicht als rationale Zahlenverhältnisse (Bruchzahlen) darstellen lassen. Im Rahmen seiner Musiktheorie bewies er die Irrationalität der Quadratwurzeln
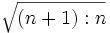 . Er zeigte dazu unter Verwendung des größten gemeinsamen Teilers und des Euklidischen Algorithmus den Satz, dass es keine Zahl geben kann, die ein geometrisches Mittel zwischen zwei im Verhältnis (n + 1):n stehenden Zahlen ist. Dies belegt, dass er bereits wesentliche Teile der Arithmetik, die in Euklids Elementen dargelegt ist, kannte. Der Satz und Beweis des Archytas wurde in der musiktheoretischen Schrift Teilung des Kanons von Euklid überliefert und verallgemeinert.
. Er zeigte dazu unter Verwendung des größten gemeinsamen Teilers und des Euklidischen Algorithmus den Satz, dass es keine Zahl geben kann, die ein geometrisches Mittel zwischen zwei im Verhältnis (n + 1):n stehenden Zahlen ist. Dies belegt, dass er bereits wesentliche Teile der Arithmetik, die in Euklids Elementen dargelegt ist, kannte. Der Satz und Beweis des Archytas wurde in der musiktheoretischen Schrift Teilung des Kanons von Euklid überliefert und verallgemeinert.Schon Hippokrates von Chios versuchte das Problem der "Verdopplung des Würfels" zu lösen. Er führte es aber auf ein Verhältnisproblem zurück. Nach Antiochos von Askalon wurde dieses Problem dann von Archytas mit Hilfe einer geometrischen Konstruktion gelöst, einer Kurve, die seinen Namen trägt.
Die Kurve des Archytas
Die Kurve des Archytas ist die erste krumme Kurve (das heißt in keiner Ebene enthalten), die man in der Geschichte der Mathematik findet. Sie wurde von Archytas zur Lösung des Problems der Verdoppelung des Würfels eingeführt. Auf seine Gleichung kommt man folgendermaßen. Gegeben sind zwei Segmente a, b, die mit u e v im Verhältnis stehen, d.h.: a:u = u:v = v:b.
Wenn man diese Werte in der Proportion auswechselt, erhält man folgendes Verhältnis:
Es sind Oberflächengleichungen. Die erste ist ein Torus, die anderen beiden sind Zylinder und ein Konus. Wenn man jetzt diese Kurve, die Archytaskurve, auf die xy-Ebene projiziert, dann ist ihre Gleichung in Polarkoordinaten (ρ,θ) die folgende:
Musik
Archytas wollte die Harmonik (Intervalltheorie) auf eine neue mathematische Grundlage stellen. Er versuchte, die Proportionen für die Konsonanzen Oktave (2:1), Quinte (3:2) und Quarte (4:3) auf axiomatischem Weg zu beweisen, was für ihn nötig war, da in seiner Akustik eine experimentelle Bestimmung der Geschwindigkeitsverhältnisse als Ursache für die Intervalle unmöglich war. Seine Axiome und Beweise überlieferte Euklid in seiner Teilung des Kanons, darin als Hilfssatz den oben zitierten Satz des Archytas über die Irrationalität der Wurzel aus (n + 1):n. Musikalisch besagt dieser Satz, dass man die Oktave (2:1), Quinte (3:2), Quarte (4:3) und andere Intervalle mit der Proportion (n + 1):n nicht exakt halbieren kann, wenn man kommensurable Größen zugrundelegt. Dieser Sachverhalt wurde in der pythagoreischen Musiktheorie bis in die Neuzeit hinein angenommen und tradiert. Die Intervalltheorie des Archytas enthält aber an anderer Stelle einen Fehler und ist zudem rein hypothetisch, was schon Aristoxenos heftig kritisierte. Daher wurde sie zur Herleitung der Intervallproportionen in der späteren Musiktheorie (Ptolemaios) abgelehnt.
Ptolemaios überlieferte auch drei Tetrachorde des Archytas mit Saitenlängen, aus denen sich die Intervall-Proportionen wie folgt berechnen lassen:
-
enharmonisches Tetrachord: (28:27)(36:35)(5:4) chromatisches Tetrachord: (28:27)(15:14)(6:5) diatonisches Tetrachord: (28:27)(8:7)(9:8)
Archytas benutzte also – im Gegensatz zur pythagoreischen Hauptströmung nach Philolaos und Euklid – schon die reine große und kleine Terz 5:4 und 6:5, die in der Mehrstimmigkeit der Neuzeit wichtig wurden.
Physik
Apuleius gibt in seiner Apologie ein von Archytas behandeltes physikalisches Argument wieder, das die Natur der Lichtreflexion auf einem Spiegel betrifft. Archytas meinte (wie Platon), dass unsere Augen Strahlen aussenden, die sich aber mit nichts vereinen können.
Archytas stellte eine Theorie zur Akustik auf und formulierte Beobachtungen und Hypothesen über den Schall. Sie enthalten Fehler, stellen aber dennoch eine bedeutende Leistung dar und wurden zur Basis der Schalltheorie von Platon und Aristoteles. Als Ursache der Töne sah er Bewegungen von Körpern sowie der Luft und als Ursache der Tonhöhe eine unterschiedliche Ausbreitungsgeschwindigkeit des Schalls (bei höherer Geschwindigkeit ein höherer Ton). Damit begründete er auch die Hypothese der Sphärenharmonie, wonach auch sich bewegende Himmelskörper Töne erzeugen, die aber wegen ihrer außerordentlichen Stärke unhörbar sind, denn der Schall kann nicht ins Ohr eindringen wie bei einem enghalsigen Gefäß, in das man viel eingießen will. Seine unhaltbare akustische Theorie wurde von Aristoxenos heftig kritisiert und aufgrund dieser Kritik von Euklid verbessert und auf Frequenzen von Schwingungen umgestellt.
Mechanik
Archytas wurde als Begründer der Mechanik betrachtet. Er soll zwei außerordentliche mechanische Apparate erfunden haben, einen mechanischen Vogel (die berühmte Taube des Archytas) und eine Kinderschelle. Von der Taube berichtet der Schriftsteller Aulus Gellius (Noctes Atticae 10.12.8-10). Der Forscher Wilhelm Schmidt hat versucht, sie nachzubauen.[11] Es handelte sich anscheinend um eine hohle Taube aus Holz, die mit Pressluft gefüllt war. Sie war mit einem Ventil versehen, welches das Öffnen und Schließen durch ein Gegengewicht ermöglichte. Wenn man die Taube auf einen Baum setzte, flog sie von Ast zu Ast, weil durch das Öffnen des Ventils der Aufstieg ermöglicht wurde; aber wenn sie auf einem anderen Ast ankam, schloss sich das Ventil von selbst oder wurde von dem, der das Gegengewicht betätigte, geschlossen.[12]
Das zweite Spielzeug, die Rassel, ist noch heute im Gebrauch. Oft sieht man sie auf Jahrmärkten. In der Originalform bestand sie aus einem kleinen Zahnrad, das an einem Stäbchen befestigt war. An diesem Rad war eine Feder befestigt, die mit einem Stück Holz verbunden war.
Archytas soll auch – schon vor Archimedes – den Flaschenzug erfunden haben.
Rezeption
Aristoteles setzte sich intensiv mit der Philosophie des Archytas auseinander und nahm dazu in einer besonderen Schrift aus drei Büchern, die verloren ist, Stellung. Außerdem verfasste er eine (verlorene) Gegenüberstellung von Platons Dialog Timaios und der Schriften des Archytas. Sein Schüler Aristoxenos, der aus Archytas’ Heimatstadt Tarent stammte, schrieb eine Biographie seines berühmten Landsmanns, die ebenfalls verloren ist. Auf ihr fusst wohl die spätere biographische und doxographische Tradition, darunter die kurze Archytas-Biographie des Diogenes Laertios. Cicero lobte die Selbstbeherrschung des Archytas. Mit dem religiösen Aspekt der pythagoreischen Tradition wurde Archytas erst in der Spätantike in Verbindung gebracht. Im Mittelalter wurde er dann als einer der großen Weisen der Antike und auch als Magier dargestellt.[13]
Als vorbildlicher Charakter und politischer Realist spielt er sowohl in Wielands Roman Geschichte des Agathon von 1796 als auch in Ratjens Das Glück auf der Kugel von 1948 eine tragende Rolle.
Textausgabe
- Carl A. Huffman: Archytas of Tarentum. Pythagorean, Philosopher and Mathematician King, Cambridge 2005. ISBN 0-521-83746-4 [grundlegende Studie; enthält Ausgabe der Fragmente mit englischer Übersetzung und ausführlichem Kommentar und Zusammenstellung aller übrigen Quellenzeugnisse]
Literatur
- Charles H. Kahn: Pythagoras and the Pythagoreans. A Brief History, Indianapolis 2001. ISBN 0-87220-576-2
Weblinks
- Literatur von und über Archytas von Tarent im Katalog der Deutschen Nationalbibliothek
- Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
Anmerkungen
- ↑ Zur Datierung Huffman S. 5f.
- ↑ Nach anderen, weniger glaubwürdigen Angaben war der Name des Vaters Mnesagoras, Mnasagetes oder Mnesarchos. Siehe dazu Huffman S. 6.
- ↑ Huffman S. 6-8.
- ↑ Huffman S. 12-14.
- ↑ Huffman S. 32-42.
- ↑ Huffman S. 19-21.
- ↑ Ein Verzeichnis bietet Holger Thesleff: An Introduction to the Pythagorean Writings of the Hellenistic Period, Åbo 1961, S. 8-11.
- ↑ Huffman S. 30-32.
- ↑ Huffman S. 68-76.
- ↑ Huffman S. 22-24, 541-550.
- ↑ Siehe dazu Wilhelm Schmidt: Aus der antiken Mechanik, in: Neue Jahrbücher für das Klassische Altertum 13 (1904) S. 329-351.
- ↑ Huffman S. 570-579.
- ↑ Huffman S. 4, 25.
Personendaten NAME Archytas von Tarent KURZBESCHREIBUNG griechischer Staatsmann, Philosoph und Mathematiker GEBURTSDATUM zwischen 435 und 410 v. Chr. STERBEDATUM zwischen 355 und 350 v. Chr.
Wikimedia Foundation.