Feldenergie

In der Physik spielt der Begriff des Feldes eine zentrale Rolle. Ein Feld besteht in einem Raum, der leer oder stofferfüllt sein kann, und messbaren physikalischen Eigenschaften, die jedem Raumpunkt zugeordnet werden können. Diese physikalischen Größen nennt man Feldgrößen. Die Feldgrößen können auch vektoriell sein, wie bei der Geschwindigkeit.

„Ein wirkliches Feld ist eine mathematische Funktion, die wir verwenden, um die Vorstellung der Fernwirkung zu vermeiden. … Ein wirkliches Feld ist dann ein System von Zahlen, die wir so festlegen, dass das, was an einem Punkt geschieht, nur von den Zahlen an diesem Punkt abhängt. Wir brauchen nichts darüber zu wissen, was anderswo vor sich geht.“

– Richard Feynman: Vorlesungen über Physik, Band II, Kap. 15-4.

Beispiele

Man verwendet den Feldbegriff in allen Zweigen der Physik. Beispiele sind

• Elektrisches Feld
• Magnetfeld
• (Konservatives) Kraftfeld
• Schallfeld
• Temperaturfeld
• Geschwindigkeitsfeld
• Dichtefeld
• Gravitationsfeld
• Feldtheorie

Motivation des Begriffs

Die Motivation zur Einführung des Feldbegriffs liegt

1. einerseits in der einfacheren Beschreibung physikalischer Vorgänge in Vielteilchensystemen. Statt alle Orte und Geschwindigkeiten der Einzelteilchen angeben zu müssen, ermöglicht die Feldbeschreibung eine elegante Methode, Temperatur und Dichte eines Gases oder einer Flüssigkeit zu behandeln.
2. andererseits in der Beachtung der Nahwirkung, die wegen der endlichen Übertragungsgeschwindigkeit physikalischer Ereignisse und Wechselwirkungen in Betracht gezogen werden muss. Das Feld besteht dann aus nicht weiter reduzierbaren physikalischen Größen, wie im elektromagnetischen Feld und im Gravitationsfeld.

Einteilung der Felder

Eine andere Einteilung von Feldern ist ihre mathematische Natur:

• Skalarfelder haben Skalare als Feldgrößen, wie die Massedichte und die Temperatur. Ein wichtiges Skalarfeld ist das Potential
• Vektorfelder haben Vektoren als Feldgrößen, wie die elektrische Feldstärke und die Kraft
• Tensorfelder haben Tensoren als Feldgrößen, wie die Elastische Spannung
• Spinorfelder haben Spinoren als Feldgrößen, wie die Stromdichte in relativistischer Feldbeschreibung (Dirac-Feld); auch Felder mit Spinoren höherer Ordnung sind beschreibbar
• statische Felder besitzen Feldgrößen, die zeitunabhängig sind. Sie sind beispielsweise Gegenstand von Statik, Elektrostatik, Magnetostatik, Hydrostatik und Aerostatik.
• stationäre Felder besitzen Feldgrößen, die zeitlich konstant sind. Sie beschreiben beispielsweise ein Magnetfeld um einen ruhenden, von einem konstanten Gleichstrom durchflossenen unveränderlichen Leiter oder eine stationäre Strömung einer Flüssigkeit (oder eines als inkompressibel betrachteten Gases).
• quasistationär nennt man Felder, wenn die zeitliche Veränderung ihrer Feldgrößen für die aktuelle Betrachtung vernachlässigbar gering ist.

Anwendung

Magnetische Feldlinien in der Umgebung eines Stabmagneten, sichtbar gemacht mit Eisenfeilspänen auf Papier

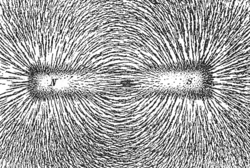
Im praktischen Umfeld finden die Vektorfelder die größte Verbreitung. Sie können besonders anschaulich mit Hilfe von Feldlinien beschrieben werden, deren Tangenten in jedem Raumpunkt die Richtung der Feldgrößen (Vektoren) darstellen. Die Feldstärke, also die Beträge der Feldvektoren in den Raumpunkten, wird durch die Dichte der Feldlinien dargestellt. Solche Feldlinien können in Experimenten verdeutlicht werden, man denke an das magnetische Feld, das mittels Eisenfeilspänen dargestellt werden kann.

Feldlinien können von bestimmten Punkten im Raum ausgehen (den Quellen) und in anderen Punkten verschwinden (den Senken). Solche Felder heißen Quellenfelder. Beispiel hierfür ist das elektrostatische Feld einer positiven und negativen elektrischen Ladung.

Feldlinien anderer Felder können nur in sich geschlossen auftreten. Man spricht dann von einem Wirbelfeld. Beispiel hierfür ist das Magnetfeld.

Siehe auch: Teilchen

Kennlinienfelder

Eine etwas andere Bedeutung kann das Wort Feld in der Elektronik bzw. Elektrotechnik haben. Dort ist der Begriff Kennlinienfeld gebräuchlich, wenn die Strom-Spannungs-Kennlinie eines elektronischen Bauteils durch einen oder mehrere Parameter beeinflusst werden kann. Dann gibt es zu jedem möglichen Wert der steuernden Parameter eine eigene Kennlinie, oder anders ausgedrückt: Jedem Wert der steuernden Parameter wird eine Kennlinie zugeordnet. Aus dieser formalen Ähnlichkeit ist der Name Kennlinienfeld verständlich.

Ein besonders markantes Beispiel hierfür ist der Transistor. Er verfügt über drei Anschlüsse, die Basis (B), den Emitter (E) und den Kollektor (C). Der Strom I_C, der den Kollektor verlässt, wird dabei durch die Spannung zwischen Emitter und Kollektor - also U_CE - reguliert, der Kollektorstrom I_C ist eine Funktion der Emitter-Kollektor-Spannung I_C = f(U_CE) (ausgangsseitige Strom-Spannungs-Kennlinie des Transistors). Die Form der Kennlinie kann aber durch die Basis-Emitter-Spannung U_BE gesteuert werden, d.h. jedem möglichen Wert für die Basis-Emitter-Spannung ist eine eigenen Kennlinie zugeordnet. Man spricht hier auch von dem Ausgangskennlinienfeld^[1] des Transistors.

Einzelnachweise

1. ↑ Der Transistor auf http://www.elektroniktutor.de