Flächenberechnungen

Physikalische Größe
Name	Flächeninhalt Oberfläche Querschnittsfläche
Formelzeichen der Größe	A, S, Q
Abgeleitet von	Länge
Größen- und Einheiten- system Einheit Dimension SI Quadratmeter (m2) L2 CGS Quadratzentimeter (cm2) L2 Planck Planck-Fläche ħ·G·c-3 Anglo- amerikanisch sq.in., sq.ft., sq.yd., sq.mi., … L2
Siehe auch: Oberfläche, Querschnitt, Querschnittsfläche

Der Flächeninhalt ist in der Geometrie ein Maß für die Größe einer Fläche. Eine Fläche ist ein zweidimensionaler, also flacher Gegenstand (Figur/Objekt ohne Rauminhalt) der eben oder gekrümmt sein kann. Sie kann einen dreidimensionalen Körper begrenzen aber nicht füllen. Der Flächeninhalt wird jedoch oft kurz Fläche genannt. Um den Flächeninhalt anzugeben, wird eine Reihe von Flächenmaßen verwendet. Das in Mathematik und Physik übliche Formelzeichen 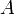$A\,$ leitet sich vom lateinischen area (= Grundfläche) ab.

Flächeninhalte – auch Querschnitte – verschiedener geometrischer Figuren

Figur/Objekt	Bezeichnungen	Flächeninhalt 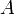$A\,$
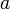
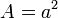
Quadrat	Seitenlänge $a\,$	$A = a^2\,$
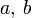
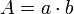
Rechteck	Seitenlängen $a,\,b$	$A = a \cdot b$
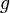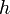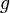
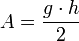
Dreieck (siehe auch: Dreiecksfläche)	Grundseite $g\,$, Höhe $h\,$, rechtwinklig zu $g\,$	$A = \frac{g \cdot h}{2}$
Trapez	zueinander parallele Seiten 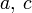$a,\,c$, Höhe 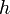$h\,$, rechtwinklig zu 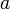$a\,$ und $c\,$	$A = \frac{a + c}{2} \cdot h$
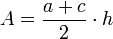
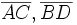
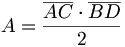
Raute	Diagonalen $\overline{AC}, \overline{BD}$	$A = \frac{\overline{AC} \cdot \overline{BD}}{2}$
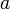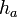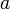
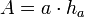
Parallelogramm	Seitenlänge $a\,$, Höhe $h_a\,$, rechtwinklig zu $a\,$	$A = a \cdot h_a$
Kreis (siehe auch: Kreisfläche)	Radius $r\,$	$A = \pi r^2\,$
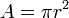
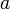
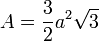
Sechseck	Seitenlänge $a\,$	$A = \frac{3}{2} a^2 \sqrt 3$

Die Bestimmung von unregelmäßigen Flächen erfolgt mittels Planimetrie.

Die Fläche unter einer Kurve y=f(x) berechnet man mit Hilfe der Integralrechnung.

Berechnung des Flächeninhalts im Raum

• Aus ebenen Teilflächen zusammengesetzte Flächen (z.B. Oberflächen von Polyedern) lassen sich aus den obigen Flächen zusammensetzen und dann wie in der Ebene behandeln.
• Oberfläche der Kugel mit Radius 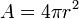$r\,$: $A=4\pi r^2\,$ (siehe auch: Kugeloberfläche)
• Für andere gekrümmte Flächen, die sich mit Hilfe differenzierbarer Funktionen beschreiben lassen, kann der Flächeninhalt mit den Mitteln der Elementaren Differentialgeometrie ermittelt werden.

Siehe auch

• Größenordnung (Fläche)
• Flächenmaß

• Grenzfläche
• Grundfläche