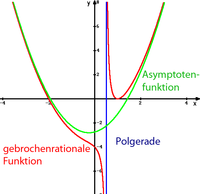
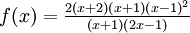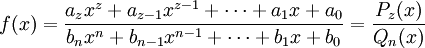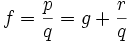Gebrochenrationale Funktion

rot: Graph der gebrochenrationalen Funktion f mit $f(x)=\tfrac{2(x + 2)(x + 1)(x - 1)^2}{(x + 1)(2x - 1)}$
blau: Polgerade durch die Polstelle bei x = 0.5
grün: Asymptotenfunktion g mit g(x) = x² + x / 2 − 11 / 4, stetig behebbare Definitionslücke bei x = − 1

Eine rationale Funktion, ist in der Mathematik eine Funktion, die sich in der Form

$f(x)=\frac{a_z x^z+a_{z-1} x^{z-1}+\cdots +a_1x+a_0}{b_n x^n+b_{n-1} x^{n-1}+\cdots +b_1x+b_0} = \frac{P_z(x)}{Q_n(x)}$

mit natürlichen Zahlen n und z schreiben lässt, also als Quotient zweier Polynome darstellbar ist.

Einteilung

• Ist das Nennerpolynom Q_n vom Grad 0, also n = 0 und ist P_z nicht das Nullpolynom, so spricht man von einer ganzrationalen Funktion oder von einer Polynomfunktion.
• Ist n > 0 , so handelt es sich um eine gebrochen rationale Funktion.
  • Ist n > 0 und z < n, so handelt es sich um eine echt gebrochen rationale Funktion.
  • Ist n > 0 und z ≥ n, so handelt es sich um eine unecht gebrochen rationale Funktion. Sie kann über Polynomdivision in eine ganzrationale Funktion und eine echt gebrochen rationale Funktion aufgeteilt werden (siehe unten).

Asymptotisches Verhalten

Für das Verhalten für x gegen Unendlich sind die Grade z bzw. n des Zähler- bzw. Nenner-Polynoms entscheidend:

Für 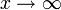$x\to\infty$ geht f(x)

• gegen 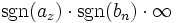$\sgn(a_z)\cdot\sgn(b_n)\cdot\infty$, falls z > n, wobei mit sgn() das Vorzeichen des Summanden mit der größten Potenz jeweils in Zähler und Nenner gemeint sind (für Genaueres über sgn() siehe Signum),
• gegen a_z / b_n, falls z = n (parallel zur x-Achse),
• gegen 0 (x-Achse), falls z < n,
• schräg verlaufende Asymptote bei dem Sonderfall z = n + 1.

Kurvendiskussion

Anhand des Funktionsterms der rationalen Funktion 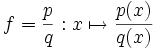$f={p\over q}:x\mapsto \frac{p(x)}{q(x)}$ lassen sich folgende Aussagen zum Funktionsgraphen machen.

Symmetrie

Eine Polynomfunktion (ganzrationale Funktion) ist gerade/ungerade, wenn alle Exponenten gerade/ungerade sind. Sind Zählerpolynom p und Nennerpolynom q von einem dieser beiden Typen, so ist auch die rationale Funktion f gerade oder ungerade:

• Sind p und q beide gerade oder beide ungerade, so ist f gerade (d.h. symmetrisch zur y-Achse)
• Ist p gerade und q ungerade, so ist f ungerade (d.h. punktsymmetrisch zum Ursprung); gleiches gilt, wenn p ungerade und q gerade ist.

In allen anderen Fällen sind Symmetrieeigenschaften von f schwieriger zu entscheiden. Siehe auch Kurvendiskussion.

Definitionsbereich, Nullstellen und Polstellen

Die gebrochen rationale Funktion ist an den Nullstellen des Nennerpolynoms q nicht definiert.

Die Nullstellen einer gebrochen rationalen Funktion werden durch die Nullstellen des Zählerpolynoms p bestimmt.

Ein Spezialfall ergibt sich, wenn eine reelle Zahl 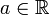$a\in\R$ gleichzeitig Nullstelle des Zählerpolynoms und des Nennerpolynoms ist. Dann sind Zähler- und Nennerpolynom durch den zugehörigen Linearfaktor x − a (eventuell sogar mehrfach) teilbar.

• Kommt x − a im Nenner öfter vor als im Zähler, so liegt eine Polstelle vor;
• andernfalls hat die rationale Funktion an der Stelle a eine stetig behebbare Definitionslücke

Asymptote

Durch die Polynomdivision von p durch q erhält man 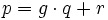$p = g\cdot q + r$ mit Polynomen g und r, wobei der Grad von r kleiner als der von q ist. Das asymptotische Verhalten von

$f = {p\over q} = g + {r\over q}$

ist damit durch die Polynomfunktion ("Asymptotenfunktion") g bestimmt (die konkrete Durchführung der Polynomdivision ist nur bei 3. und 4. notwendig):

1. z < n => x-Achse ist Asymptote: g(x) = 0
2. z = n => waagerechte Asymptote: $g(x) = \frac{a_z}{b_n}$
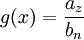
3. z = n + 1 => schräge Asymptote: 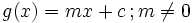$g(x) = mx + c \,; m \ne 0$ (Spezialfall von 4)
4. z > n + 1 => ganzrationale Näherungsfunktion

Siehe auch

• Partialbruchzerlegung
• Meromorphe Funktion
• Charakteristik