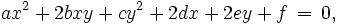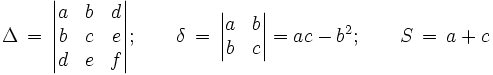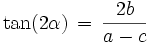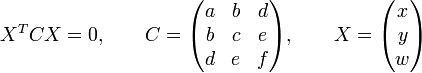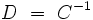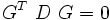Kegelschnitte

Schnitt eines Kegels mit einer Ebene

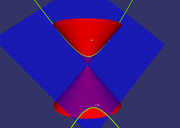
Ein Kegelschnitt (englisch conic section, cone-plane intersection) ist eine Kurve, die entsteht, wenn man die Oberfläche eines unendlichen Kegels bzw. Doppelkegels mit einer Ebene schneidet. Ein Kegelschnitt ist der zweidimensionale Sonderfall einer Quadrik.

Klassifikation der Kegelschnitte

Kegelschnitte

Wenn die Schnittebene die Kegelspitze nicht enthält, können folgende Figuren entstehen:

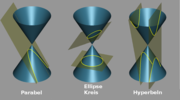
• Eine Ellipse, wenn die Schnittebene zu keiner Mantellinie parallel ist. Dies bedeutet, dass der Winkel zwischen Achse und Schnittebene größer als der halbe Öffnungswinkel des Kegels ist. Ist dieser Winkel ein Rechter, so tritt der Kreis als Spezialfall einer Ellipse auf.
• Eine Parabel, wenn die Schnittebene zu genau einer Mantellinie des Kegels parallel ist. Dies bedeutet, dass der Winkel zwischen Achse und Ebene gleich dem halben Öffnungswinkel ist.
• Eine Hyperbel, wenn die Schnittebene zu zwei Mantellinien des Kegels parallel ist. Dies bedeutet, dass der Winkel zwischen Achse und Ebene kleiner als der halbe Öffnungswinkel ist.

Wenn die Schnittebene durch die Kegelspitze geht, entstehen die ausgearteten Kegelschnitte:

• Ein Punkt, wenn die Schnittebene den Kegel nur in der Spitze schneidet (ausgeartete Ellipse).
• Eine Gerade, wenn die Schnittebene den Kegel entlang einer Mantellinie berührt (ausgeartete Parabel).
• Zwei einander schneidende Geraden, wenn die Schnittebene zwei Mantellinien enthält (ausgeartete Hyperbel).

Die allgemeine Kegelschnittgleichung

Im ebenen kartesischen Koordinatensystem ist der Graph einer quadratischen Gleichung (mit den Variablen x und y), falls er nicht leer ist, immer ein Kegelschnitt. Umgekehrt können alle Kegelschnitte durch solche Gleichungen beschrieben werden. Die allgemeine Gleichung für Kegelschnitte lautet also

$a x^2 + 2 bx y + c y^2 + 2 d x + 2 e y + f \, = \, 0,$

wobei der Faktor 2 bei den Koeffizienten b, d und e aus Gründen der Zweckmäßigkeit verwendet wird.

Der Typ des Kegelschnitts ergibt sich aus den im Folgenden definierten Determinanten Δ und δ sowie der Summe S:

$\Delta \, = \, \begin{vmatrix} a & b & d \\ b & c & e \\ d & e & f \end{vmatrix}; \qquad \delta \, = \, \begin{vmatrix} a & b \\ b & c \end{vmatrix} = ac-b^2; \qquad S \, = \, a + c$

• Für δ > 0 und 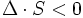$\Delta \cdot S < 0$ handelt es sich um eine Ellipse. Gilt zusätzlich a = c und b = 0, so ist diese Ellipse sogar ein Kreis.

• Gelten die Bedingungen δ < 0 und 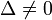$\Delta \ne 0$, so ergibt sich eine Hyperbel, die im speziellen Fall a + c = 0 gleichseitig (rechtwinklig) ist.

• Unter den Voraussetzungen δ = 0 und 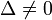$\Delta \ne 0$ beschreibt die Gleichung eine Parabel.

• Wenn Δ = 0 und δ = 0 kommt ein paralleles Geradenpaar heraus.

• Ist Δ = 0 und δ > 0 kommt ein imaginäres Geradenpaar heraus.

• Sollte Δ = 0 und δ < 0 kommt als Lösung ein reelles Geradenpaar heraus.

Soweit es sich um eine Ellipse, Hyperbel oder Parabel handelt, bedeutet die Bedingung b = 0, dass die Achsen parallel zu den Koordinatenachsen verlaufen. Im allgemeinen Fall lässt sich der Drehwinkel gegenüber der achsenparallelen Lage durch

$\tan (2 \alpha) \, = \, \frac{2 b}{a - c}$

berechnen.

Folgerungen aus der allgemeinen Kegelschnittsgleichung:

• Ein Kegelschnitt ist durch fünf Punkte eindeutig festgelegt.

• Zwei verschiedene Kegelschnitte schneiden einander höchstens in vier Punkten.

Besonders elegant wird die Kegelschnittgleichung unter Verwendung homogener Koordinaten: Alle Punkte X, die auf dem Kegelschnitt mit der Matrix C liegen, erfüllen die homogene Kegelschnitt-Gleichung:

$X^T C X = 0 , \qquad C = \begin{pmatrix} a &amp;amp;amp; b &amp;amp;amp; d \\ b &amp;amp;amp; c &amp;amp;amp; e \\ d &amp;amp;amp; e &amp;amp;amp; f \end{pmatrix}, \qquad X = \begin{pmatrix} x \\ y \\ w \end{pmatrix}$

Die Matrix C definiert hierbei den Kegelschnitt vollständig und wird daher oft selbst auch als Conic bezeichnet. Für alle X, die die obige Gleichung nicht erfüllen, gibt das Vorzeichen des Ergebnisses darüber Aufschluss, ob der Punkt innerhalb/außerhalb (bzw. auf welcher Seite) des Conics liegt. Wie viele andere Objekte der projektiven Geometrie auch, ändert eine Skalierung der Matrix nichts an den Objekteigenschaften, die Multiplikation mit einem negativen Wert ändert allerdings die Interpretation von innen und außen.

Die oben beschriebenen Kegelschnitte sind sogenannte Punkt-Conics, d. h., alle Punkte, die auf der Kurve liegen, erfüllen die Gleichung. Invertiert man nun die Matrix C, gelangt man zum dualen Conic (oder Linien-Conic)

$D \ = \ C^{-1}$

Alle Geraden G (in homogener Darstellung), die Tangenten an den Punkt-Conic sind, erfüllen die Gleichung

$G^T \ D \ G = 0$

Die Conic-Matrix ist eine implizite Form der Kurve oder der Menge von Tangenten. Man kann sehr leicht prüfen, ob ein Punkt X auf dem Kegelschnitt liegt oder nicht, aber die Form liefert keine Parametrisierung zum „Entlanglaufen“. Ohne eine Parametrisierung ist es nicht direkt möglich, die Menge aller Punkte zu finden, die auf dem Objekt liegen, bzw. das Objekt selbst darstellen. Man kann jedoch alle Kegelschnitte durch algebraische Umformungen in eine explizite Form überführen und erhält damit geeignete Parametrisierungen.

Anwendungen und Beispiele

Kegelschnitt in der Architektur: Kathedrale von Brasilia

Eine Anwendung finden die Kegelschnitte in der Astronomie, da die Bahnen der Himmelskörper genäherte Kegelschnitte sind.

Auch in der Optik werden sie verwendet - als Rotationsellipsoid für Autoscheinwerfer, als Paraboloid oder Hyperboloid für Spiegelteleskope usw.

Geschichtliches

Der griechische Mathematiker Menaichmos untersuchte an Platons Akademie die Kegelschnitte mit Hilfe eines Kegelmodells. Er fand dabei heraus, dass sich das delische Problem auf die Bestimmung des Schnittpunkts zweier Kegelschnitte zurückführen lässt. Euklid schrieb vier Bücher über Kegelschnitte, die uns aber nicht erhalten sind. Die gesamten Kenntnisse der antiken Mathematiker über die Kegelschnitte fasste Apollonios von Perge in seinem achtbändigen Werk Konika zusammen. Die Beschreibung von Kegelschnitten durch Koordinatengleichungen wurde von Fermat und Descartes eingeführt.

Siehe auch

Kegelstumpf, Korbbogen, Kurve, Himmelsmechanik, Zweikörperproblem, projektive Geometrie, Drehquadrik.

Weblinks

• Animierte Kegelschnitte bei EXOPAS
• http://www.unet.univie.ac.at/~a9907818/kegelsch.htm
• Graphische Darstellung der Kegelschnitte und Namensgebung

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3