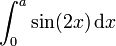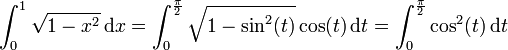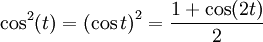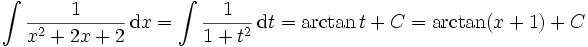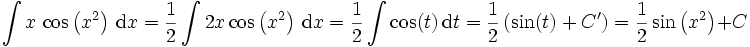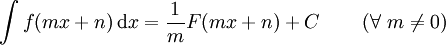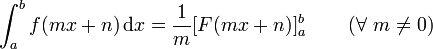- Lineare Substitution
-
Die Integration durch Substitution oder Substitutionsregel ist eine wichtige Methode in der Integralrechnung, um Stammfunktionen und Integrale zu berechnen. Durch Einführung einer neuen Integrationsvariablen wird ein Teil des Integranden ersetzt, um das Integral zu vereinfachen und so letztendlich auf ein bekanntes (oder einfacher handhabbares) Integral zurückzuführen.
Sei I ein reelles Intervall,
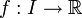 eine stetige Funktion und
eine stetige Funktion und ![\varphi: [a,b] \to I](/pictures/dewiki/48/0126defd729569c2c85c7612cf544d3f.png) stetig differenzierbar. Dann ist
stetig differenzierbar. Dann istDie Substitutionsregel ist die Umkehrung der Kettenregel aus der Differentialrechnung; entsprechend kehrt die partielle Integration die Produktregel um. Ihr Äquivalent für mehrdimensionale Integrale ist der Transformationssatz, der allerdings eine bijektive Substitutionsfunktion voraussetzt.
Inhaltsverzeichnis
Beweis
Sei F eine Stammfunktion von f. Nach der Kettenregel gilt für die Ableitung der zusammengesetzten Funktion

Durch zweimalige Anwendung des Hauptsatzes der Differential- und Integralrechnung erhält man damit die Substitutionsregel:
Praktische Berechnung
Für die praktische Ausführung der Substitutionsregel hat sich ein Verfahren herausgebildet, das recht leicht zu merken ist und (unter Verwendung von rein symbolischen Notationen) aus der Substitutionsregel hervorgeht, dessen Gültigkeit aber nicht unmittelbar auf den ersten Blick klar ist. Ist ein Integral der Form
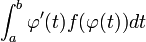
zu berechnen, so bezeichnen wir f stets als äußere Funktion, φ als innere Funktion, ihre Ableitung φ' als innere Ableitung.
Vorstellung des Verfahrens
Oftmals ist einem Integral nicht sofort "anzusehen", ob und in welcher Weise die Substitutionsregel anzuwenden ist, da man die "innere Ableitung" φ'(t) nicht auf den ersten Blick erkennt bzw. diese noch geschickt ergänzt werden muss. Ein recht simples, aber sehr typisches Beispiel für ein solches Integral ist durch
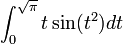
gegeben. Zwar lässt sich sin(t2) als Verkettung aus der Sinus-Funktion und der Parabel φ(t) = t2 darstellen, allerdings ist die innere Ableitung φ'(t) durch 2t gegeben, den Faktor 2 suchen wir vergeblich und müssen ihn für die Anwendung der Substitutionsregel erst ergänzen:
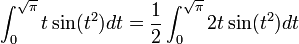
Erst jetzt können wir die Substitutionsregel anwenden:
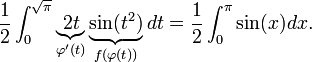
Wir erhalten das gleiche Ergebnis, wenn wir die innere Funktion φ mit der neuen Integrationsvariablen identifizieren x = t2, nach der alten Variable ableiten und die Ableitung - rein formal als Bruch aufgefasst - nach dt freistellen. Setzen wir dann dt in das Integral ein, so erhalten wir:

und somit

was mit unserem ersten Ergebnis übereinstimmt. Dies ist die Grundidee eines Verfahrens der Substitution, das immer dann funktioniert, wenn die innere Funktion innerhalb der Integrationsgrenzen bijektiv ist und ihre Ableitung auf dem gesamten Integrationsbereich von 0 verschieden ist oder zumindest höchstens auf Nullmengen, z.B. in einzelnen Punkten, den Wert 0 annimmt. Aufgrund seiner großen Bedeutung ist das Verfahren so bekannt, dass nicht selten dieses Verfahren mit der Substitutionsregel gleichgesetzt wird. Es besteht in der Ausführung der folgenden Schritte
- Wähle eine Funktion als innere Funktion und identifiziere sie mit der neuen Integrationsvariablen x = φ(t)
- Bilde die Ableitung dx / dt = φ'(t), fasse dx / dt als Bruch auf und stelle nach dt frei:
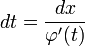 . Ersetze dt in dem gegebenen Integral durch diesen Ausdruck.
. Ersetze dt in dem gegebenen Integral durch diesen Ausdruck.
- Stelle die Gleichung x = φ(t) nach t frei: t = φ − 1(x) (hier benötigt man die Bijektivität von φ!) und ersetze die alte Integrationsvariable t stets durch φ − 1(x).
- Ersetze die Integrationsgrenzen a und b durch φ(a) und φ(b).
Oftmals bietet es sich an, mehrere Schritte in einem auszuführen. Das Verfahren beruht zwar auf der Substitutionsregel, ist aber leichter zu merken und vermeidet das Problem, die innere Ableitung bzw. eine mögliche Ergänzung einer inneren Ableitung auf einen Blick erkennen zu müssen. Die Wahl der inneren und äußeren Funktion ist bei einem gegebenen Integral in der Regel nicht eindeutig. Vielmehr kommt es in praktischen Rechnungen häufig auf eine möglichst geschickte Wahl der inneren Funktion an, da nur in diesem Fall das durch Substitution umgeformte Integral leichter zu berechnen ist als das Ausgangsintegral.
Es sei angemerkt, dass bei konsequenter Ausführung der obigen Schritte "Mischintegrale" auftreten (also solche, die sowohl die alte wie auch die neue Integrationsvariable enthalten). Diese sind rein symbolisch zu verstehen und - streng genommen - mathematisch nicht wohldefiniert.
Beispiel
Zu berechnen sei das Integral
Wir wählen als innere Funktion
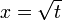 . Dann gilt:
. Dann gilt:Wir erhalten:
Umstellen der Gleichung
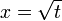 nach t liefert: t = x2, wir ersetzen:
nach t liefert: t = x2, wir ersetzen:Substituieren der Grenzen und Vereinfachung des Integranden liefert dann das Integral:
Es ergibt sich also insgesamt:
wobei sich die letzte Gleichheit aus der Anwendung der partiellen Integration folgt. Bei diesem Beispiel erreicht man rechnerische Vereinfachung, wenn man nicht streng den Regeln des Verfahrens folgt. Da wir
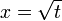 gesetzt haben, hätten wir direkt Ausdrücke der Form
gesetzt haben, hätten wir direkt Ausdrücke der Form 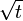 durch x ersetzen können, anstatt die Gleichung
durch x ersetzen können, anstatt die Gleichung 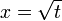 nach t aufzulösen und das Ergebnis dann einzusetzen. Man beachte, dass aufgrund der Integrationsgrenzen
nach t aufzulösen und das Ergebnis dann einzusetzen. Man beachte, dass aufgrund der Integrationsgrenzen 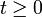 und damit
und damit 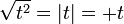 gilt.
gilt.Begründung
Sei ein Integral der Form
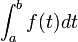
zu berechnen. Wir gehen davon aus, dass wir bereits einen erfolgversprechenden Kandidaten für eine innere Funktion
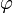 gefunden haben, die bijektiv ist und deren Ableitung auf [a,b] höchstens in Nullmengen den Wert 0 annimmt. Bezogen auf obiges Beispiel wäre also etwa
gefunden haben, die bijektiv ist und deren Ableitung auf [a,b] höchstens in Nullmengen den Wert 0 annimmt. Bezogen auf obiges Beispiel wäre also etwa  und
und 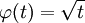 .
.Wir werden nun das Integral unter Verwendung der Substitutionsregel umformen, ohne das oben beschriebene Verfahren anzuwenden.
Zunächst gibt es wegen der Bijektivität von
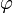 ihre Umkehrfunktion
ihre Umkehrfunktion 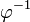 und wir können wegen
und wir können wegen 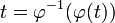 schreiben:
schreiben:
Nun erweitern wir mit der inneren Ableitung (hier benötigen wir, dass
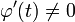 gilt):
gilt):
Wir wenden erneut die Identität
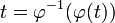 an und es ergibt sich:
an und es ergibt sich: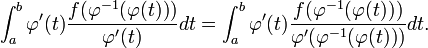
Auf den letzten Ausdruck ist die Substitutionsregel anwendbar. Mit
 gilt:
gilt: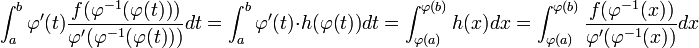
Nun betrachten wir das gleiche Problem, wenden aber diesmal das Verfahren an. Wir setzen also
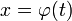 und berechnen die Ableitung:
und berechnen die Ableitung:
Einsetzen in das Integral liefert:
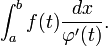
Nun lösen wir die Gleichung
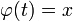 nach t auf:
nach t auf: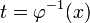
und setzen ein:
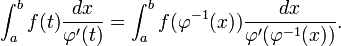
Substituieren der Grenzen liefert letztlich:

was mit dem Ergebnis übereinstimmt, das wir durch die Kettenregel gewonnen haben: das Verfahren funktioniert. In praktischen Rechnungen ist das Verfahren nur dann von Erfolg gekrönt, wenn der Ausdruck
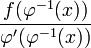 leichter zu integrieren ist als der ursprüngliche Integrand, was sich häufig darin äußert, dass viele Terme sich gegenseitig "wegkürzen" oder aber ein unbekanntes Integral durch Substitution auf ein bekanntes, bereits gelöstes Problem zurückgeführt werden kann.
leichter zu integrieren ist als der ursprüngliche Integrand, was sich häufig darin äußert, dass viele Terme sich gegenseitig "wegkürzen" oder aber ein unbekanntes Integral durch Substitution auf ein bekanntes, bereits gelöstes Problem zurückgeführt werden kann.Substitution eines bestimmten Integrals
Beispiel 1
Berechnung des Integrals
für eine beliebige reelle Zahl a > 0: Durch die Substitution
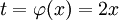 erhalten wir
erhalten wir 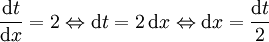 und:
und: 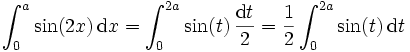
![= \frac{1}{2} [ -\cos(t) ]_0^{2a} = \frac{1}{2} (-\cos(2a)+\cos(0)) = \frac{1}{2}(1 - \cos(2a))](/pictures/dewiki/50/2d1d14f1af47a61a238879a8763876e5.png) .
.Beispiel 2
Berechnung des Integrals
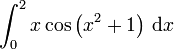 :
:
Durch die Substitution
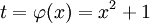 erhalten wir
erhalten wir 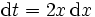 und
undMan beachte, dass die untere Grenze des Integrals x = 0 in t = 02 + 1 = 1 umgewandelt wurde und die obere Grenze x = 2 in t = 22 + 1 = 5.
Beispiel 3
Berechnung des Integrals
Man substituiert
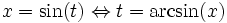 , was zu
, was zu 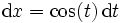 führt und mit
führt und mit 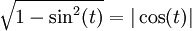 die letzte Gleichung ergibt:
die letzte Gleichung ergibt:Das Ergebnis kann mit Partieller Integration oder mit der trigonometrischen Formel
und einer weiteren Substitution berechnet werden.
Substitution eines unbestimmten Integrals
Unter den obigen Voraussetzungen gilt
Nachdem man eine Stammfunktion der substituierten Funktion bestimmt hat, macht man die Substitution rückgängig und erhält eine Stammfunktion der ursprünglichen Funktion.
Beispiele
Beispiel 1
Mit der Substitution x = t − 1, dx = dt erhält man
Beispiel 2
Mit der Substitution t = x2,
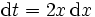 erhält man
erhält manMan beachte, dass die Substitution nur für
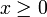 bzw. nur für
bzw. nur für  streng monoton ist.
streng monoton ist.Spezialfälle der Substitution
Logarithmische Integration
Integrale mit der speziellen Form Zähler des Integranden ist Ableitung des Nenners können sehr einfach mit Hilfe der logarithmischen Integration gelöst werden, was einen Spezialfall der Substitutionsmethode darstellt:
Lineare Substitution
Integrale mit linearen Verkettungen können wie folgt berechnet werden:
Für das bestimmte Integral gilt entsprechend
Siehe auch
- Partielle Integration für eine weitere wichtige Regel zur Berechnung von Integralen,
- Generalsubstitution für Funktionen, die trigonometrische Funktionen enthalten.
Weblinks
Wikimedia Foundation.

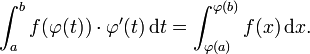
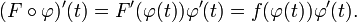
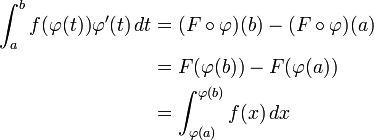
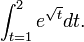
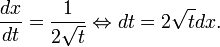
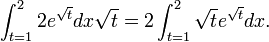
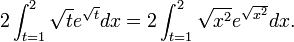
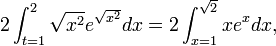
![\int_{t=1}^{2} e^ {\sqrt{t}}dt = 2 \int_{x=1}^{\sqrt{2}} x e^x dx = 2 \left[ e^x (x-1) \right ]_1^\sqrt2,](/pictures/dewiki/55/799f4a810b2f7837d0ff24ce72d11d2a.png)