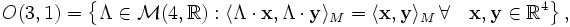Lorentzgruppe

Die Lorentz-Gruppe O(3,1) (benannt nach dem niederländischen Mathematiker und Physiker Hendrik Antoon Lorentz) ist eine Lie-Gruppe in der Mathematik, die vielfache Anwendungen in der Physik, insbesondere der Relativitätstheorie, findet.

Definition

Die Lorentz-Gruppe ist die lineare Invarianzgruppe des Minkowskiraumes 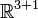$\mathbb{R}^{3+1}$, der ein vierdimensionaler Vektorraum mit einem Pseudo-Skalarprodukt ist. Die Lorentz-Gruppe ist die Menge aller linearen Automorphismen des Minkowskiraumes, die das Pseudo-Skalarprodukt erhalten.

Sie ähnelt damit in ihrer Definition der Gruppe der Drehspiegelungen O(3) im dreidimensionalen Raum, die aus den linearen Automorphismen des R³ besteht, die das Standard-Skalarprodukt erhalten und damit Längen und Winkel.

Der wesentliche Unterschied besteht jedoch darin, dass die Lorentz-Gruppe nicht die Längen und Winkel im dreidimensionalen Raum erhält, sondern die bezüglich des indefiniten Pseudo-Skalarprodukts im Minkowskiraum definierten Längen und Winkel. Insbesondere erhält sie Eigenzeitabstände in der speziellen Relativitätstheorie.

Formal können wir daher definieren (definierende Darstellung):

$O(3,1)=\left\{ \Lambda \in \mathcal{M}(4,\mathbb{R}): \langle \Lambda\cdot \mathbf{x},\Lambda\cdot \mathbf{y}\rangle_M= \langle \mathbf{x},\mathbf{y} \rangle_M \, \forall \quad \mathbf{x},\mathbf{y} \in \mathbb{R}^{4}\right\},$

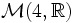wobei $\mathcal{M}(4,\mathbb{R})$ die reellen 4×4 Matrizen und 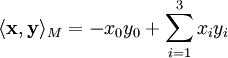$\langle \mathbf{x},\mathbf{y}\rangle_M=- x_0 y_0 + \sum_{i=1}^3 x_iy_i$ das Pseudo-Skalarprodukt bezeichnet.

Eigenschaften

Die Lorentz-Gruppe ist eine 6-dimensionale Lie-Gruppe. Sie ist nicht kompakt.

Die räumlichen Drehspiegelungen bilden als die Fixpunktgruppen zeitartiger Vektoren eine Untergruppe der Lorentz-Gruppe. Solche Untergruppen sind nicht normal, die Untergruppen zu verschiedenen Fixpunkten (das entspricht verschiedenen Inertialsystemen) sind zueinander konjugiert.

Die Lorentz-Gruppe sondern besteht aus vier Zusammenhangskomponenten. Elemente derselben Zusammenhangskomponente gehen durch Anwendung von infinitesimalen Transformationen auseinander hervor. Im Gegensatz dazu stehen die diskreten Transformationen, die Elemente verschiedener Zusammenhangskomponenten miteinander verbinden: Spiegelungen, Raumspiegelungen, Zeitspiegelungen und Raum-Zeit-Spiegelungen. Die Untergruppe SO(3,1) der Elemente mit Determinante 1 heißt eigentliche Lorentz-Gruppe und enthält zwei der vier Zusammenhangskomponenten. Die eigentliche orthochrone Lorentz-Gruppe ist die Zusammenhangskomponente die die Identität enthält.

Jedes Element der eigentlichen orthochronen Lorentz-Gruppe lässt sich durch zwei Elemente einer Untergruppe räumlicher Rotationen O_1,2 und eine spezielle Lorentztransformation (= Boost in die x₁-Richtung ) Λ in der Form O₁ΛO₂ darstellen.

Die eigentliche orthochrone Lorentz-Gruppe ist nicht einfach zusammenhängend, d.h. nicht jede geschlossene Kurve kann stetig auf einen Punkt zusammengezogen werden. Die universelle einfach zusammenhängende Überlagerung der eigentlichen orthochronen Lorentz-Gruppe ist die komplexe spezielle lineare Gruppe SL(2,C) (diese Gruppe findet Anwendung in der Physik bei der Theorie der projektiven Darstellungen der O(3,1) in Quantentheorien).

Lie-Algebra

Die sechsdimensionale Lie-Algebra der O(3,1) wird in der definierenden Darstellung durch die drei infinitesimalen Erzeuger der räumlichen Rotationen J_i und durch die drei infinitesimalen Erzeuger der Lorentz-Boosts K_i aufgespannt. Diese Lie-Algebra ist isomorph zur Lie-Algebra sl(2,C):

[J_i,J_j] = ε_ijkJ_k

[K_i,K_j] = − ε_ijkJ_k

wobei die Erzeuger J_i der Rotationen eine Lie-Unteralgebra bilden, nämlich die so(3).

Beispiele

Vektorfeld auf R2	Ein-parametrige Untergruppe von SL(2,C), Möbius Transformationen	Ein-parametrige Untergruppe von SO+(1,3), Lorentz Transformationen	Vektorfeld auf R4
Parabolisch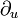
$\partial_u\,\!$	$\left[ \begin{matrix} 1 & \alpha \\ 0 & 1 \end{matrix} \right]$	$\left[ \begin{matrix} 1+\alpha^2/2 & \alpha & 0 & -\alpha^2/2 \\ \alpha & 1 & 0 & -\alpha \\ 0 & 0 & 1 & 0 \\ \alpha^2/2 & \alpha & 0 & 1-\alpha^2/2 \end{matrix} \right]$	$X_1 = \,\!$ $x (\partial_t + \partial_z) + (t-z) \partial_x \,\!$
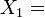
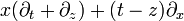
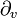
$\partial_v\,\!$	$\left[ \begin{matrix} 1 & i \alpha \\ 0 & 1 \end{matrix} \right]$	$\left[ \begin{matrix} 1+\alpha^2/2 & 0 & \alpha & -\alpha^2/2 \\ 0 & 1 & 0 & 0 \\ \alpha & 0 & 1 & -\alpha \\ \alpha^2/2 & 0 & \alpha & 1-\alpha^2/2 \end{matrix} \right]$	$X_2 = \,\!$ $y (\partial_t + \partial_z) + (t-z) \partial_y \,\!$
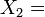
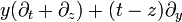
Hyperbolisch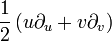
$\frac{1}{2} \left( u \partial_u + v \partial_v \right)$	$\left[ \begin{matrix} \exp \left(\frac{\beta}{2}\right) & 0 \\ 0 & \exp \left(-\frac{\beta}{2}\right) \end{matrix} \right]$	$\left[ \begin{matrix} \cosh(\beta) & 0 & 0 & \sinh(\beta) \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \sinh(\beta) & 0 & 0 & \cosh(\beta) \end{matrix} \right]$	$X_3 = \,\!$ $z \partial_t + t \partial_z \,\!$
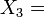
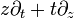
Elliptisch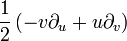
$\frac{1}{2} \left( -v \partial_u + u \partial_v \right)$	$\left[ \begin{matrix} \exp \left( \frac{i \theta}{2} \right) & 0 \\ 0 & \exp \left( \frac{-i \theta}{2} \right) \end{matrix} \right]$	$\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) & 0 \\ 0 & \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]$	$X_4 = \,\!$ $-y \partial_x + x \partial_y \,\!$
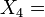
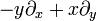
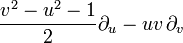
$\frac{v^2-u^2-1}{2} \partial_u - u v \, \partial_v$	$\left[ \begin{matrix} \cos \left( \frac{\theta}{2} \right) & -\sin \left( \frac{\theta}{2} \right) \\ \sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{matrix} \right]$	$\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta) & 0 & \sin(\theta) \\ 0 & 0 & 1 & 0 \\ 0 & -\sin(\theta) & 0 & \cos(\theta) \end{matrix} \right]$	$X_5 = \,\!$ $-x \partial_z + z \partial_x \,\!$
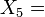
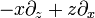
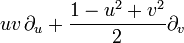
$u v \, \partial_u + \frac{1-u^2+v^2}{2} \partial_v$	$\left[ \begin{matrix} \cos \left( \frac{\theta}{2} \right) & i \sin \left( \frac{\theta}{2} \right) \\ i \sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{matrix} \right]$	$\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \cos(\theta) & -\sin(\theta) \\ 0 & 0 & \sin(\theta) & \cos(\theta) \end{matrix} \right]$	$X_6 = \,\!$ $-z \partial_y + y \partial_z \,\!$

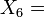
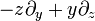
Siehe auch

• Lorentztransformation