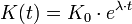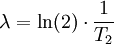Mooresche Gesetz

Grafik zur Belegung des mooreschen Gesetzes mit Intel-Prozessoren (Stand 2004; Ordinate ist logarithmisch skaliert). Kritiker bemängeln, dass die Kostenoptimalität dieser Prozessoren nicht gezeigt wurde.

Das mooresche Gesetz (engl. Moore's Law; „Gesetz“ im Sinne von „Gesetzmäßigkeit“) sagt aus, dass sich die Komplexität integrierter Schaltkreise mit minimalen Komponentenkosten etwa alle zwei Jahre verdoppelt. Unter Komplexität verstand Gordon Moore, der das Gesetz 1965 formulierte, die Anzahl der Schaltkreiskomponenten auf einem Computerchip. Ursprünglich sprach Moore von einer jährlichen Verdoppelung, 1975 korrigierte er seine Angabe auf eine Verdoppelung alle zwei Jahre (siehe auch wirthsches Gesetz).

Nach der heute vorherrschenden, abgewandelten Auslegung sagt das mooresche Gesetz aus, dass sich die Anzahl an Transistoren auf einem handelsüblichen Prozessor alle achtzehn Monate verdoppelt. Gelegentlich ist auch von einer Verdoppelung der Integrationsdichte die Rede, also der Anzahl an Transistoren pro Flächeneinheit. Dieser Technologiefortschritt bildet eine wesentliche Grundlage der „digitalen Revolution“. Diese Auslegung des mooreschen Gesetzes bildet heute den Rahmen, an dem die Halbleiterindustrie ihre Entwicklungspläne auf mehrere Jahre hinaus festmacht.

Auf Intels Entwicklerforum (IDF) im Herbst 2007 sagte Moore das Ende seines „Gesetzes“ voraus: es werde wahrscheinlich noch 10 bis 15 Jahre Bestand haben, bis eine fundamentale Grenze erreicht ist. Allerdings wurde ein halbes Jahr später von Pat Gelsinger, Chef der Digital-Enterprise-Sparte von Intel prognostiziert, dass das mooresche Gesetz noch bis 2029 Gültigkeit behalten soll.

Geschichte

Gordon Moore äußerte seine Beobachtung 1965 in einem Artikel der Zeitschrift Electronics ^[1], nur wenige Jahre nach Erfindung der integrierten Schaltung. Die Bezeichnung mooresches Gesetz wurde um 1970 von Carver Mead geprägt. Ursprünglich sagte Moore eine jährliche Verdoppelung voraus, korrigierte diese Aussage jedoch 1975 in einer Rede vor der Society of Photo-Optical Instrumentation Engineers auf eine Verdoppelung alle zwei Jahre. Auslöser dafür war, dass sich die stürmische Entwicklung der Halbleitertechnik der ersten Jahre verlangsamt hatte. In den Medien ist meist von einer Verdoppelung der Integrationsdichte alle 18 Monate die Rede, woher diese Zahl stammt, ist jedoch ungewiss.

Auslegung

Moores Gesetz ist kein wissenschaftliches Naturgesetz, sondern eine Faustregel, die auf eine empirische Beobachtung zurück geht. Gleichzeitig kann man von einer „sich selbsterfüllenden Prophezeiung“ ^[2] sprechen, da verschiedenste Industriezweige an der Entwicklung besserer Mikrochips beteiligt sind. Sie müssen sich auf gemeinsame Meilensteine einigen (z. B. optische Industrie mit verbesserten lithographischen Methoden), um wirtschaftlich arbeiten zu können. Die Formulierung des mooreschen Gesetzes hat sich im Laufe der Zeit stark verändert. Sprach Moore noch von der Komponentenanzahl auf einem integrierten Schaltkreis, so ist heute von der Transistorenanzahl auf einem integrierten Schaltkreis die Rede, mitunter sogar von der Transistorenanzahl pro Flächeneinheit.

mooresches Gesetz – Die Abhängigkeit der Kosten pro Bauelement von der Packungsdichte.

Moore stellte fest, dass die Kosten einer Schaltkreiskomponente verfahrensbedingt mit sinkender und steigender Komponentenanzahl anstiegen. Bei niedriger Komponentenanzahl wurde das verfügbare Material nicht voll ausgenutzt, für höhere Komponentenanzahlen mussten experimentelle Verfahren eingesetzt werden, die sich wirtschaftlich noch nicht lohnten. Er bezog seine Beobachtung daher ausschließlich auf das jeweilige Kostenoptimum, also dasjenige Produktionsverfahren und diejenige Komponentenanzahl pro Schaltkreis, bei denen die Kosten pro Schaltkreiskomponente am geringsten ausfielen. Dadurch ist theoretisch klar vorgegeben, welches Herstellungsverfahren und welcher Computerchip zur Überprüfung von Moores Gesetz in jedem Jahr betrachtet werden müssten.

Die unterschiedlichen Formulierungen verzerren die ursprüngliche Beobachtung Moores teilweise bis zur Unkenntlichkeit. Bereits die variable Auslegung des Verdoppelungszeitraums von 12, 18 oder 24 Monaten verursacht beträchtliche Unterschiede. Da Computerchips stark in der Größe variieren, ist es auch durchaus nicht dasselbe, ob man die Transistorenanzahl pro Chip oder pro Flächeneinheit betrachtet. Das Weglassen des Kostenoptimums schließlich führt zu einer vollständigen Entfremdung. Ohne Kostenoptimum kann jedes beliebige Produktionsverfahren und jeder beliebige Schaltkreis zur Bestätigung von Moores Gesetz herangezogen werden; ob es sich um einen handelsüblichen Prozessor, extrem teure Hochtechnologie oder experimentelle Schaltkreise, die noch gar nicht käuflich erwerblich sind, handelt, ist in dieser laxen Auslegung ohne Belang. Durch die unterschiedlichen kursierenden Versionen hat Moores Gesetz viel von seiner objektiven Aussagekraft eingebüßt.

Schreibweise

Die Komplexitätszunahme K in Abhängigkeit von der Zeit t des mooreschen Gesetzes folgt einem Exponentialgesetz:

$K(t) = K_0 \cdot e^{\lambda \cdot t}$

Dabei ist die Rate der Zunahme λ der Kehrwert der Verdopplungszeit T₂, multipliziert mit der Konstanten ln(2):

$\lambda = \operatorname{ln}(2) \cdot \frac{1}{T_2}$

Ist also die Verdoppelungszeit T₂ = 2 Jahre, so beträgt λ = 0,35 · 1/Jahr.

Rechenleistung

Dass mit der Anzahl der Transistoren auf einem Computerchip auch die Rechenleistung der Computer exponentiell anwächst, kann aus dem mooreschen Gesetz nicht gefolgert werden. Bei modernen Prozessoren werden immer mehr Transistoren für einen integrierten Speicher (Cache) verwendet, der zur Rechenleistung nur passiv beiträgt, indem er Zugriffe auf häufig benötigte Daten beschleunigt. Als Beispiel sei hier der Vergleich des Pentium-III 500 MHz mit einer 1-GHz-Variante angegeben, bei der die Leistungssteigerung mit dem Faktor 2,3 erst mit einer Verdreifachung der Transistoranzahl und Verdoppelung der Taktrate erreicht wurde.

Prozessor	Transistoren	SPEC-Werte
		Ganzzahl	Gleitkomma
Pentium-III 500 MHz (externer L2-Cache)	9,5 Mio.	20,6	14,7
Pentium-III 1000 MHz (interner L2-Cache)	28,5 Mio.	46,8	32,2

In Mehrkernprozessoren werden mehrere Prozessorkerne auf einem Chip zusammengeführt, die parallel arbeiten und dadurch mehr Leistung erbringen. Hier wird die Verdoppelung der Transistorenanzahl hauptsächlich durch die Verdoppelung der Anzahl der Prozessorkerne erreicht. Auch hier tritt jedoch keine Verdoppelung der Rechenleistung ein, denn beim Parallelbetrieb der Prozessorkerne fällt zusätzlicher Koordinierungsaufwand an, der die Leistung wieder schmälert.

Technische Grenzen

Neben Kritik an der fehlerhaften Auslegung des Gesetzes selbst gab es immer wieder Stimmen, die das Ende der Wirksamkeit der mooreschen Faustregel aufgrund unüberwindbarer technischer Hürden voraussagten. Bislang wurden jedoch alle prognostizierten Hürden überwunden, bevor sie einen Knick der mooreschen Exponentialkurve verursachen konnten. Entwicklungspläne, die die Einhaltung des mooreschen Gesetzes sicherstellen sollen, reichen bis ins Jahr 2020 (laut SEMATech).

2005 lief die konkurrenzfähige Herstellung der Chips für den Weltmarkt mit Strukturen zwischen 130 und 90 nm. In Vorbereitung für die Massenfertigung befand sich die 65-nm-Technik. Im Entwicklungslabor befasste man sich bereits mit deutlich kleineren Strukturgrößen. So wurden schon erste Prototyp-Transistoren mit nur 10 nm Gatelänge gefertigt – das beschrieb eine Veröffentlichung von Robert Chau auf der 61^st Device Research Conference in Salt Lake City, Utah, am 23. Juni 2003. Solche Transistoren würden für die 22-nm-Herstellungstechnik gebraucht, die nach dem mooreschen Gesetz 2011 zum Einsatz kommen soll.^[3]

Zum Vergleich: Transistoren aus der Halbleiterfertigung mit 90 nm haben eine Gatelänge von ca. 50 nm und sind etwa so groß wie ein Influenzavirus. Bei der Herstellung werden solch kleine Strukturen über lithographische Belichtung erreicht. Für immer höhere Auflösungen wird derzeit an „nassen“ Belichtungsverfahren gearbeitet. Die sogenannten Immersionsverfahren sollen die nötige Auflösung für die Fertigung in der nahen Zukunft sicherstellen. Für noch kleinere Strukturen bei der 32-nm-Fertigung und danach wird ein komplett neues Belichtungsverfahren nötig: EUV. Diese gegenwärtig noch nicht technisch hinreichend umsetzbare EUV-Technik arbeitet mit 13 nm Wellenlängen. EUV ist die gängige Abkürzung für „extremes Ultraviolett“, auch „weiche“ Röntgenstrahlung genannt. EUV kann Glas nicht durchdringen, kann also nicht mit Linsen fokussiert werden, sondern nur über Hohlspiegel reflektiert werden. Ein Hohlspiegel, mit dem dies möglich ist, wurde jüngst bei Carl Zeiss SMT entwickelt. Die Spiegeloberfläche muss extremen Anforderungen entsprechen. Es gilt Abweichungswerte von nur 0,15 nm zu erreichen. Damit handelt es sich um den derzeit „weltweit ‚präzisesten‘ Spiegel“. ^[4]

Ende März 2006 kündigte Intel den Start der Massenfertigung mit 45-nm-Technologie für Ende 2007 an – zu diesem Zeitpunkt produzierte der Hauptmitbewerber AMD mit 65 nm. Ungefähr zur selben Zeit gab IBM bekannt, dass es mit tief ultravioletten Laserstrahlen (DUV-Lithografie) gelungen sei, Strukturgrößen von 29,5 nm zu erreichen. Während die zuvor angesprochene EUV-Technik (32 nm) zu diesem Zeitpunkt noch weitestgehend unerprobt war, konnten die IBM-Forscher mittels DUV schon erste Erfolge erzielen – damit scheint das mooresche Gesetz auch weiterhin seine Gültigkeit zu behalten. Der Pressesprecher des Chip-Herstellers Intel gibt sich optimistisch: »Es gibt so viele verschiedene Möglichkeiten, die Materialien, die Fertigungsprozesse und den Aufbau der Transistoren zu optimieren. […] Da ist noch viel dabei, ehe Moore′s Gesetz am Ende ist.«^[5]

Obwohl der Fortschritt für die nächsten Jahre gesichert scheint, mehren sich heute die Stimmen, die eine Verlangsamung der Zunahme der Integrationsdichte in naher Zukunft erwarten. Zum einen werde eine technische Grenze erreicht, wenn ein Transistor die Ausdehnung weniger Atome erreiche (siehe auch Tunnelstrom). Zum anderen wachse der finanzielle Aufwand zur Entwicklung und Herstellung integrierter Schaltkreise schneller als die Integrationsdichte, so dass es einen Punkt geben werde, an dem die Investitionen sich nicht mehr rentieren würden. Bei Annahme eines exponentiellen Wachstums der Entwicklungskosten wäre gleichermaßen eine Grenze durch das verfügbare Kapital vorgegeben. Auch Quantencomputer könnten das mooresche Gesetz durchbrechen. Der Übergang zu Quantenrechnern könnte die technische Bedeutung von Transistoren so stark mindern, dass deren Anzahl nicht mehr als Maßzahl der Komplexität taugt.

Im Bereich höchster Rechneranforderungen (speziell: CFD bzw. numerische Strömungssimulation) ist dagegen seit etwa 2003 eine deutliche Verletzung des Moore'schen Gesetzes zu beobachten. Auf Basis eines Benchmarks einer kommerziellen CFD-Software durchgeführt im Zeitraum von 1996 bis 2009 zeigt sich deutlich, dass die Zeit die je Finitem Volumen (cell) und je Iteration des Solvers benötigt wird, etwa ab 2003 gar nicht oder nur noch marginal sinkt (ca. 10% nach 2 Jahren statt der dem Moor'schen Gesetz entsprechenden 50%, z.T. weniger bis 0%). Die Prozessorhersteller haben diese Misere schon längst erkannt und entsprechend mit Mehrkern(Cores)-CPUs reagiert. Dem einfachen PC-Anwender wird suggeriert, dass durch die höhere Anzahl der Kerne auch seine Rechnerleistung steige, was nur marginal der Fall ist und auch nur sein kann, da der überwiegende Teil der Software nicht für (Prozessor-) parallele Nutzung programmiert ist. Anders verhält es sich im Bereich der Strömungssimulation (CFD). Hier sind die meisten Softwarewerkzeuge parallelisiert und skalieren bei entsprechender Netzwerktechnolgie (Infiniband, Myrinet o.ä.) bzw. schneller Informationsverbindung zwischen den Cores recht linear, d.h. x-mal mehr Cores bedeutet auch x-mal so schnell. Damit sind dem Speedup bei der Anwendung nur durch die Latenzzeiten im Netzwerk zwischen den Cores Grenzen gesetzt. Allerdings sind bei kommerzieller Software zusätzliche Softwarelizenzen zu erwerben, da hier meist nach Anzahl der genutzten Cores unterschieden wird.

Futurologie

Futurologen wie Raymond Kurzweil halten das mooresche Gesetz für einen Spezialfall eines allgemeineren Gesetzes, nach dem die gesamte technologische Evolution verlaufe: Ist das Potenzial einer speziellen Technologie ausgeschöpft, so wird sie von einer neuen abgelöst.

Kurzweil bezieht sich in seiner kritischen Erörterung des mooreschen Gesetzes nicht auf „Transistoren pro Chip“, sondern auf die „Rechenleistung pro 1000-Dollar-Computer“. Betrachtet man die Entwicklung von mechanischen Rechenmaschinen, über Röhren und Transistoren bis zum heutigen Mikroprozessor, zeige dies eine doppelt exponentielle Steigerung der Leistungsfähigkeit. (Für kürzere Zeiträume ist die einfach-exponentielle Steigerung jedoch noch eine gute Approximation). Die Rechenleistung pro 1000 Dollar verdoppelte sich in den Jahren 1910 bis 1950 im Abstand von drei Jahren (mechanische Rechenmaschinen), von 1950 bis 1966 etwa alle zwei Jahre und jetzt etwa jährlich (Stand: 2003).

Aufgrund dieser Beobachtung vermuten einige Futurologen, dass Computer die Rechenleistung des menschlichen Gehirns übertreffen werden und mit einer leistungsfähigen künstlichen Intelligenz die technische Entwicklung derart beschleunigen könnten, dass der Mensch diese nicht mehr begreifen würde. Dieser Zeitpunkt wird technologische Singularität genannt.

Einzelnachweise

1. ↑ G. E. Moore: Cramming more components onto integrated circuits. In: Electronics. 19, Nr. 3, 1965, S. 114–117 (PDF). 
2. ↑ Gordon Moore bezeichnet sein Gesetz als eine „self fulfilling prophecy“, siehe Gordon Moore Says Aloha to Moore's Law. Auf: the Inquirer. 13. April 2005, abgerufen am 4. März 2009
3. ↑ R. Chau, B. Doyle, M. Doczy, S. Datta, S. Hareland, B. Jin, J. Kavalieros, M. Metz: Silicon nano-transistors and breaking the 10 nm physical gate length barrier. In: Device Research Conference, 2003. 2003, S. 123-126. 
4. ↑ Alexander Stirn: Glatte Spiegel für kleine Chips www.sueddeutsche.de am 5.12.2007
5. ↑ Alexander Stirn: Supercomputer im Handy www.sueddeutsche.de am 15.11.2007

Literatur

• S. Hamilton: Taking Moore's law into the next century. In: Computer. 32, Nr. 1, 1999, S. 43–48 (doi:10.1109/2.738303). 
• M. Y. Lanzerotti (Hrsg.): The Technical Impact of Moore's Law. In: IEEE solid-state circuits society newsletter. 20, Nr. 3, IEEE, 2006 (HTML, PDF). 
• R. R. Schaller: Moore's law: past, present and future. In: Spectrum, IEEE. 34, Nr. 6, 1997, S. 52–59 (doi:10.1109/6.591665). 

Weblinks

• Material von Intel
  • Moore's Law – Made real by Intel innovation. Auf: Intel.com.
  • Moore’s Law 40th Anniversary. Auf: Intel.com. (umfangreiche Presseinformationen)
  • Vierzig Jahre mooresches Gesetz. Auf: Intel.com.

• Beat Döbeli Honegger: Moore’s law. In:Beats Biblionetz: Begriffe. (Beat Doebelis Begriffsnetz-Grafik und Definitions-Versionen)
• Christoph Drösser: Die Wie-schnell-wird-aus-Technik-Schrott-Form. Auf:Zeit Online. 14. April 2005
• Ray Kurzweil: The Law of Accelerating Returns. Auf: KurzweilAI.net. 7. März 2001 (Artikel in dem Kurzweil ausgehend vom mooreschen Gesetz die Beschleunigung der Technologischen Entwicklung prognostiziert).

• Meldungen auf Heise-Online:
  • Christof Windeck: Intel und Qinetiq wollen mit III-V-Halbleitern das mooresche Gesetz fortführen. Auf: Heise-Online. 8. Dezember 2005.
  • Jürgen Kuri: Vor 40 Jahren: Electronics druckt Moores Gesetz. Auf: Heise-Online. 19. April 2005 (Artikel über die Hintergründe und Umstände der Veröffentlichung).