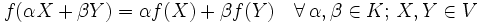- Rechenoperation
-
Ein Operator ist eine mathematische Vorschrift (ein Kalkül), durch die man aus mathematischen Objekten neue Objekte bilden kann. Er kann eine standardisierte Funktion, oder eine Vorschrift über Funktionen sein. Anwendung finden die Operatoren bei Rechenoperationen, also bei manuellen oder bei maschinellen Berechnungen.
Inhaltsverzeichnis
Operator als Verknüpfung
Standardisierte Operatoren werden in der Mathematik meist dann definiert, wenn es sich um eine häufige, immerwiederkehrende Vorschrift handelt, meist eine ein- oder zweistellige Verknüpfung. Die Argumente dieser Verknüpfung heißen Operanden. Diese Operatoren werden durch ein spezielles, kennzeichnendes mathematisches Symbol (ein spezielles Schriftzeichen der Formelschreibweise) dargestellt.
Betrachtet man beispielsweise 1 + 2, so ist « + » das Symbol des Operators und «1» und «2» sind die Operanden.
Beispiele:
- Die für die Grundrechenarten verwendeten Operatoren für Addition, der als das Pluszeichen «+» geschrieben wird, das Minus «−» für Subtraktion, die Malzeichen «·», «×» oder «*» für die Multiplikation, und die Division (Mathematik) kann mit Geteiltzeichen «÷», «:», «/» oder mit Bruchstrich geschrieben werden
- Deren Erweiterung, der Hyper-Operator
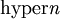
- Der einstellige Operator für die negative Zahl, der ebenfalls mit Minus «−» geschrieben wird, wie auch «+» für die positive Zahl
- Logische Operatoren:
- Junktoren, Boolesche Operatoren oder Konnektive wie «
und», «oder», «nicht» - Vergleichsoperatoren wie « < », « > », « = », «
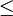 », «
», «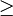 »
»
- Junktoren, Boolesche Operatoren oder Konnektive wie «
- Das Verkettungszeichen «
 » für die Komposition von Funktionen
» für die Komposition von Funktionen - Der Klassenbildungsoperator { | }
Funktionaloperatoren
Typische Operatoren für Funktionale sind:
- Der Differentialoperator
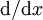 zur Bildung von Differentialen, der Volterraoperator
zur Bildung von Differentialen, der Volterraoperator 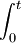 zur Bildung des bestimmten Integrals
zur Bildung des bestimmten Integrals - der Nabla-Operator
 und die Operatoren
und die Operatoren 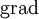 ,
, 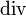 und
und 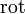 für Differentiale in Vektorfeldern
für Differentiale in Vektorfeldern
Operator als Abbildung zwischen Vektorräumen
In der Funktionalanalysis hat man es mit Vektorräumen zu tun, deren Elemente selbst Funktionen sind. Um die Elemente dieser Vektorräume besser von den Abbildungen zwischen solchen Vektorräumen zu unterscheiden, nennt man letztere auch Operatoren:
Sind V und W topologische Vektorräume, dann nennt man eine Abbildung
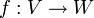 einen Operator. Ist W der Skalarenkörper des Vektorraums, dann heißt f Funktional.
einen Operator. Ist W der Skalarenkörper des Vektorraums, dann heißt f Funktional.In der Funktionalanalysis betrachtet man unter anderem Eigenschaften von linearen Operatoren, also Abbildungen
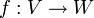 mit
mitDie im vorherigen Abschnitt beschriebenen Funktionaloperatoren sind Beispiele für Operatoren im Sinne der Funktionalanalysis. Spezielle Klassen linearer Operatoren sind etwa kompakte Operatoren oder Fredholm-Operatoren.
Operatoren der Physik
Operatoren werden auch im mathematischen Kalkül der Physik definiert:
- die Fourieranalyse, die Funktionen in andere Funktionen transformiert – hier gibt es kein explizites Symbol
- Dichteoperator ρ, Ortsoperator
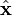 , Impulsoperator
, Impulsoperator 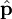 , Hamilton-Operator
, Hamilton-Operator 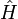 der Quantenmechanik
der Quantenmechanik
Normen
- ISO 31-11 Mathematische Zeichen und Symbole
- DIN 1304-1 Allgemeine Formelzeichen
- DIN 1302 Allgemeine mathematische Zeichen und Begriffe
- DIN 1313 Physikalische Größen und Gleichungen
- DIN 1338 Formelschreibweise
Literatur
- Formelzeichen, Formelsatz, Mathematische Zeichen und Begriffe. DIN-Taschenbuch 202. 1994-07.
Wikimedia Foundation.