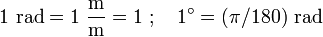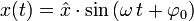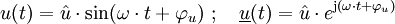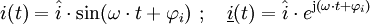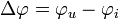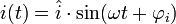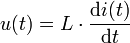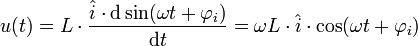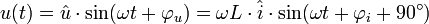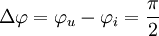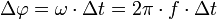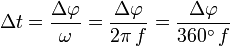Nacheilwinkel

Wenn zwei oder mehr Vorgänge periodisch sinusförmig mit gleicher Frequenz ablaufen und wenn deren Mittelwert-Durchgänge (oder deren Maxima) zeitlich versetzt auftreten, so wird der Versatz als Phasenverschiebung bezeichnet. Die Vorgänge verlaufen synchron, jedoch phasenverschoben.

Phasenverschobene Spannung und Strom an einem Kondensator (Die reelle und die imaginäre Achse sind vertauscht gezeichnet. Animation.)

Diese Erscheinung kann bei allen Vorgängen auftreten, bei denen Zeitglieder, Trägheiten oder Reaktanzen eine Rolle spielen, so vor allem in der Elektrotechnik, der Elektroakustik, der Akustik und in der Schwingungs-Mechanik.

Größenangabe der Phasenverschiebung

Motor-Typenschild mit Angabe des cos φ zur Kennzeichnung der Phasenverschiebung (rechts Mitte)

Ein sinusförmiger periodischer Ablauf einer Schwingung kann als ein sich ständig wiederholender Kreisdurchlauf betrachtet werden. Damit wird eine volle Periode mit dem vollen Kreiswinkel von 360° gleichgesetzt und die Phasenverschiebung als Winkel Δφ oder (wenn Verwechselungen ausgeschlossen sind) als φ angegeben. Dieser Winkel wird gemäß DIN 40 110-1 Phasenverschiebungswinkel genannt. Winkel werden gemäß DIN 1301-1 meistens in Radiant oder in Grad angegeben; z. B. bedeuten die Angaben „π/2 rad“, „90°“ und „eine Viertelperiode“ dieselbe Phasenverschiebung. Es ist auch möglich, das Maß der Phasenverschiebung in absoluten Zeiteinheiten oder als Längenmaß anzugeben, wenn bei dem Vorgang ein räumlicher Weg zurückgelegt wird, z. B. bei einem Lichtstrahl.

Der Richtungssinn der Phasenverschiebung einer Schwingung gegenüber der Bezugsschwingung führt auch zu der Bezeichnung von Nacheilwinkeln oder Voreilwinkeln bzw. dem Nacheilen oder Voreilen. Das wird oft mit zwei gegeneinander versetzt mit gleicher Geschwindigkeit in der komplexen Ebene rotierenden Zeigern dargestellt (siehe komplexe Wechselstromrechnung).

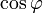In der elektrischen Energietechnik wird zur leichteren Berechnung die Phasenverschiebung als Kosinus des Phasenverschiebungswinkels $\varphi$ (phi), also $\cos \varphi$, angegeben. Der „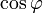$\cos \varphi$“ ist auf jedem Wechselstrommotor-Leistungsschild sowie anderen reaktiven elektrischen Verbrauchern angegeben und dient zum Beispiel zur Berechnung des Wirkleistungs-Anteils an der Gesamtleistung oder zur Bemessung von Schaltkontakten (vgl. Schaltlichtbogen).

Veranschaulichung und Messung der Phasendifferenz

Mit geeigneten Oszillographen bzw. Oszilloskopen können zwei oder mehr gegeneinander zeitlich verschobene Schwingungen als einzelne Kurven unmittelbar in ihrem zeitlichen Verlauf sichtbar gemacht werden. Die Phasenverschiebung lässt sich so aus dem zeitlichen Abstand an einem Gitter-Raster auf der Bildschirmröhre oder dem Aufzeichnungspapier direkt ablesen.

Geometrische Darstellung im Zeigerdiagramm

Alternativ legt man an den y-Eingang eines Oszilloskops und an dessen x-Ablenkung anstelle der Zeitablenkung jeweils eine Wechselspannung an, so erscheint eine sogenannte Lissajous-Figur. Ihre Form erlaubt Rückschlüsse auf die Phasenverschiebung der beiden Spannungen: Bei gleicher Phasenlage und Frequenz entsteht ein schräger Strich, bei zunehmender Phasenverschiebung eine schräge elliptische Figur, die bei einer Phasenverschiebung von 90° je nach Größe der Schwingungsamplituden zur aufrechten oder horizontalen Ellipse, oder bei gleichen Amplituden zum Kreis wird.

Das Zeigerdiagramm ermöglicht eine einfache quantitative Darstellung von Phasenverschiebungen. Damit kann auch ermittelt werden, welchen resultierenden Scheinstrom unterschiedliche Amplituden (Länge der Zeiger) und Phasenlagen (Winkel der Zeiger zueinander) zweier Ströme erzeugen.

Erscheinungsformen, Anwendungen

Elektrotechnik

Phasenverschiebung zwischen Strom und Spannung an einer Induktivität

Phasenverschiebung zwischen Strom und Spannung am Kondensator

Dreiphasenwechselstrom besteht aus drei um je 120° gegeneinander versetzt schwingenden Wechselströmen

Prüfschaltung für Phasenverschiebung an einer Induktivität

Prüfschaltung für Phasenverschiebung am Kondensator

Prüfschaltung für Phasenverschiebung am Widerstand

In der Elektrotechnik spricht man von einer Phasenverschiebung, wenn in einem Wechselstromkreis die zeitlichen Verläufe von Strom und Spannung an einem Bauteil oder die Spannungen vor und nach einem Vierpol gegeneinander verschoben sind. Das Phänomen tritt immer dann auf, wenn ein mit Wechselstrom betriebener Vierpol induktive oder kapazitive, differenzierende oder verzögernde Eigenschaften besitzt. Im Bereich hoher Frequenzen kann dafür einzig die Signallaufzeit verantwortlich sein.

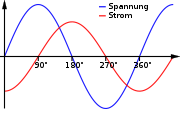
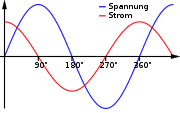
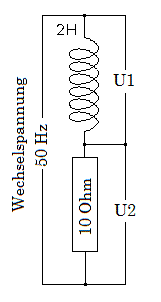
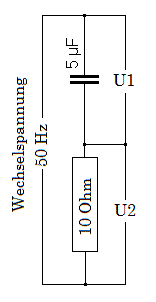
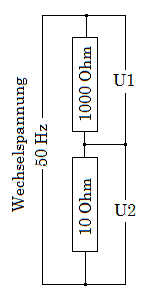
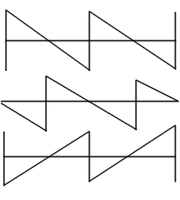
In den nebenstehenden Bildern ist U1 die Wechselspannung am jeweiligen Bauelement, U2 ist proportional zum durchfließenden Strom. Stellt man diese beiden Spannungen auf einem Zweikanal-Oszilloskop dar, stellt man fest:

• Bei der idealen Spule bzw. Induktivität hinkt der Strom der Spannung U1 um 90° nach, es tritt nur positive Blindleistung auf (die Polaritätsangabe der Blindleistung beschreibt ihre Phasenlage, nicht jedoch die Fließrichtung). Der Phasenverschiebungswinkel ist unabhängig von der Frequenz.
• Beim idealen Kondensator eilt der Strom der Spannung U1 um 90° voraus, es tritt nur negative Blindleistung auf. Der Phasenverschiebungswinkel ist unabhängig von der Frequenz.
• Beim ohmschen Widerstand sind U1 und U2 immer gleichphasig. Am Widerstand gibt es nur Wirkleistung.
• Bei einer Kombination von R, L und C kann die Phasenverschiebung beliebige Werte zwischen -90° und +90° annehmen. Der Phasenverschiebungswinkel hängt von der Frequenz ab und ändert sich besonders stark in der Nähe einer Resonanzstelle; vergleiche: Schwingkreis.

Weiterführende Erklärungen hierzu: siehe Impedanz

Hochfrequenztechnik

Hier wird die Phasenverschiebung zur Phasenmodulation verwendet. Im zweiseitigen Frequenzspektrum bedeutet das, dass der Zeiger der Signalfrequenz in wechselnde Richtungen in Bezug auf den Zeiger der Trägerfrequenz zeigt. Damit können Daten kodiert werden.

Akustik bzw. Tontechnik

Werden zwei oder mehrere Schallwellen gleicher Frequenz überlagert, so ergibt sich als resultierendes Signal je nach Phasenverschiebungswinkel ein entweder verstärktes oder gedämpftes Signal. Eine solche Überlagerung wird Interferenz genannt und ist im Schallfeld ortsabhängig: Je nach Abstand und Position der Quellen ergeben sich an unterschiedlichen Betrachterpositionen alle möglichen Kombinationen von Verstärkungen und Abschwächungen.

Mit der Festlegung der Einheiten für den ebenen Winkel in DIN 1301-1

$1\ \mathrm{rad} =1\ \frac{\mathrm m}{\mathrm m}=1\ ;\quad 1^{\circ} =(\pi/180)\ \mathrm{rad}$

ergibt sich beispielsweise für eine feste Verzögerung von Δt = 0,5 ms folgenden frequenzabhängigen Phasenverschiebungswinkel ∆φ:

∆φ	∆φ	f	λ
360°	2 π rad	2000 Hz	0,1715 m
180°	π rad	1000 Hz	0,3430 m
90°	π/2 rad	500 Hz	0,6860 m
45°	π/4 rad	250 Hz	1,372 m
22,5°	π/8 rad	125 Hz	2,744 m
11,25°	π/16 rad	62,5 Hz	5,488 m

Wellenlänge λ = c / f

Schallgeschwindigkeit c = 343 m/s bei 20 °C

Die Einheit Radiant kann weggelassen werden, wenn sie nicht zur Verdeutlichung einer Winkelangabe dienen soll.

Zum akustischen Zusammenhang von Phasenverschiebung ∆φ und Laufzeitdifferenz bei Stereofonie, ∆t siehe Laufzeitstereofonie. Mit digitaler Signalverarbeitung ist es heute möglich, die Phasenlage mehreren Lautsprechern zugeführter Signale individuell zu verstellen und damit für einen kleinen Abhörpunkt oder Messpunkt das Schallfeld gezielt zu steuern.

Andere Gebiete

In der Bautechnik wird mit Phasenverschiebung der Zeitraum zwischen dem Auftreten der höchsten Temperatur auf der Außenoberfläche eines Bauteils bis zum Erreichen der höchsten Temperatur auf dessen Innenfläche bezeichnet.

In der Optik werden Linsen entspiegelt, indem eine dünne Schicht auf der Glasoberfläche eine Doppelreflexion erzeugt, die bei einer bestimmten Wellenlänge λ eine Phasenverschiebung der beiden Reflexionen von ½ λ erreicht. Üblicherweise wird die Schichtdicke auf die Wellenlänge des gelben Lichts (λ ≈ 600 nm) eingestellt.

Mathematische Beschreibung

Gleichungen für die Schwingung und den rotierenden Zeiger

Der einfachste Fall einer Schwingung ist die harmonische Schwingung. Mathematisch lässt sie sich folgendermaßen beschreiben:

$x(t) = \hat{x}\cdot\sin\left(\omega\,t + \varphi_0 \right) \,$

wobei x(t) die Auslenkung zur Zeit t, 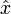$\hat x$ die Amplitude (Maximalwert der Auslenkung), ω = 2πf die Kreisfrequenz und f die Frequenz darstellen. In DIN 40 110-1 werden 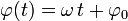$\varphi(t) =\omega \,t +\varphi_0$ als Phasenwinkel bezeichnet und 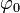$\varphi_0$ als Nullphasenwinkel.

Im Folgenden wird am Beispiel einer sinusförmigen Wechselspannung und eines sinusförmigen Wechselstroms die Phasenverschiebung gezeigt.

$u(t) = \hat u \cdot \sin(\omega \cdot t + \varphi_{u})\ ;\quad \underline u(t) = \hat u \cdot e^{\mathrm j (\omega \cdot t + \varphi_{u})} \,$

wobei u(t) der Augenblickswert der Spannung zur Zeit t, 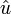$\hat u$ die Amplitude der Spannung und 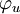$\varphi_{u}$ ihr Nullphasenwinkel sind.

Analog dazu lässt sich der elektrische Strom darstellen:

$i(t) = \hat i \cdot \sin(\omega \cdot t + \varphi_{i})\ ;\quad \underline i(t) = \hat i \cdot e^{\mathrm j (\omega \cdot t + \varphi_{i})} \,$

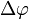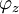Die Phasenverschiebungswinkel $\Delta \varphi$ oder $\varphi_z$ der Spannung gegenüber dem Strom ist nun die Differenz der Phasenwinkel beider Schwingungen:

$\Delta \varphi = \varphi_u - \varphi_i \,$

Ist der Phasenverschiebungswinkel gleich null, sind beide Schwingungen phasengleich.

Beispiel ideale Spule

Eine ideale Spule wird von einem sinusförmigen Wechselstrom 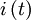$i\,(t)$ durchflossen:

$i(t) = \hat i \cdot \sin(\omega t + \varphi_{i}) \,$

Zwischen Strom und Spannung besteht an einer Spule der Zusammenhang:

$u(t) = L \cdot \frac{\mathrm{d} i(t)}{\mathrm{d}t} \,$

Daraus folgt:

$u(t) = L \cdot \frac{\hat i \cdot \mathrm{d} \sin(\omega t + \varphi_{i})}{\mathrm{d}t} = \omega L \cdot \hat i \cdot \cos(\omega t + \varphi_{i}) \,$

$u(t)= \hat u \cdot \sin(\omega t + \varphi_{u}) = \omega L \cdot \hat i \cdot \sin(\omega t + \varphi_{i} + 90^\circ)$

Eine vorgegebene sinusförmige Spannung verursacht also einen Strom mit gleicher Kurvenform. Allerdings sind die Augenblickswerte von Spannung und Strom nicht mehr phasengleich.

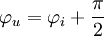$\varphi_u = \varphi_i + \frac{\pi}{2}$     bzw.     $\varphi_i = \varphi_u - \frac{\pi}{2}$

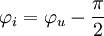
Phasenverschiebungswinkel:

$\Delta \varphi = \varphi_{u} - \varphi_{i} = \frac{\pi}{2}$

Der Strom eilt um den Phasenverschiebungswinkel 90° nach.

Zusammenhang zwischen Phasenverschiebungswinkel und Phasenlaufzeit

Der Zusammenhang zwischen dem Phasenverschiebungswinkel ∆φ und der Laufzeitdifferenz ∆t ist:

$\Delta \varphi = \omega \cdot \Delta t = 2 \pi \cdot f \cdot \Delta t$

bzw.

$\Delta t = \frac{\Delta \varphi}{\omega} = \frac{\Delta \varphi}{2 \pi \,f} =\frac{\Delta \varphi}{360^\circ \,f}$

aufgrund der oben angegebenen Umrechnungen

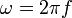$\omega = 2 \pi f \$   und   $2 \pi = 360^\circ$ .

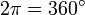Unterschied zwischen 180°-Phasenverschiebung und Verpolung

Bei einer Verpolung werden positive Halbwellen zu negativen, und negative zu positiven Halbwellen. Dabei wird die Phase nicht verschoben. Deshalb ist eine Phasenverschiebung um 180° nicht mit einer Verpolung gleichsetzbar.

Sägezahnsignale
oben: Originalsignal
mitte: 180°-phasenverschobenes Signal
unten: VerpoltesSignal

Siehe auch

• Scheinleistung
• Phasenumkehr

Weblinks

• Phasenverschiebung φ und Laufzeitdifferenz Δ t
• Rechner: Zusammenhang von Phase, Phasenwinkel, Frequenz und Laufzeit (Delay)