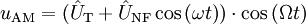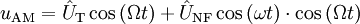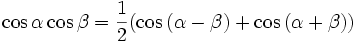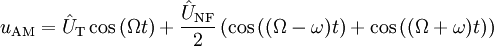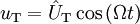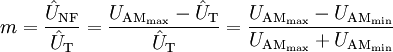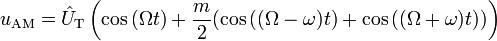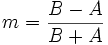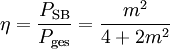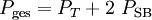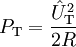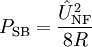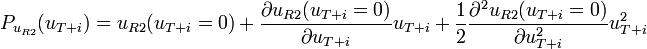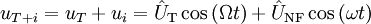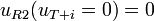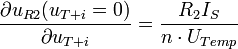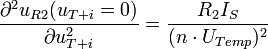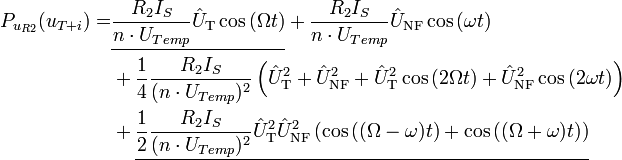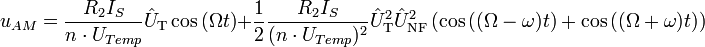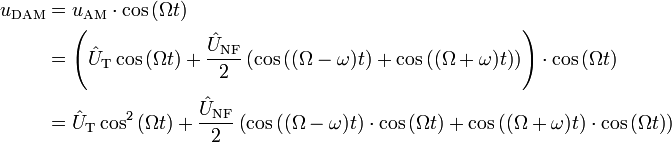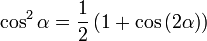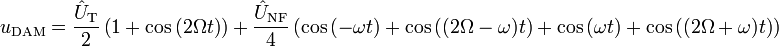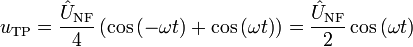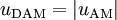Regenerativempfänger

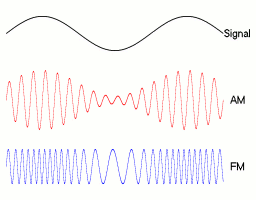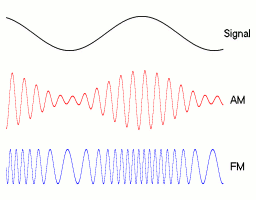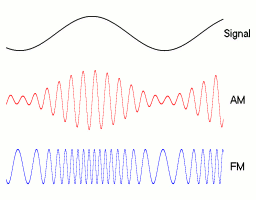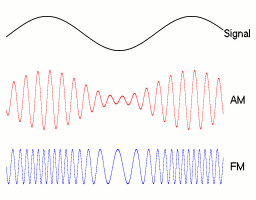
Die Amplitudenmodulation (AM) ist ein Modulationsverfahren. Dabei wird die Amplitude einer hochfrequenten Trägerwelle abhängig vom zu übertragenden, niederfrequenten (modulierenden) Nutzsignal verändert.

Niederfrequente Nutzsignale wie Sprache oder Musik können häufig nicht direkt über gewünschte Übertragungsmedien wie beispielsweise einen Funkkanal übertragen werden. Zur Übertragung muss das Nutzsignal im Frequenzbereich verschoben werden, was durch die in diesem Artikel beschriebene AM bewerkstelligt werden kann. Durch das Verschieben in unterschiedliche Frequenzbereiche können mehrere Nutzsignale gleichzeitig und ohne gegenseitige Störung übertragen werden.

Gegenüberstellung von Amplituden- und Frequenzmodulation

Anwendung der Amplitudenmodulation

AM wird verwendet bei:

• Rundfunk auf den Frequenzbändern Langwelle, Mittelwelle, Kurzwelle
• Fernsehen, abhängig von der verwendeten Fernsehnorm, siehe Fernsehsignal
• CB-Funk
• Amateurfunk (meist in Form der Einseitenbandmodulation)
• Flugnavigation (ADF)
• Flugfunk (zivil – VHF 118 bis 137 MHz, militär – UHF)
• Chopper-Verstärker

Die AM wurde zu Beginn der Rundfunktechnik eingesetzt, weil sich derartig modulierte Signale sehr einfach erzeugen und demodulieren lassen. Ebenfalls zeichnet sie sich durch einen geringen Anspruch an Bandbreite aus. So belegt bei der üblicherweise verwendeten Rundfunk-AM jeder Sender die Bandbreite 2 · 4,5 kHz = 9 kHz bzw. 2 · 5 kHz = 10 kHz. Diesen Vorteilen stehen etliche Nachteile wie Störanfälligkeit, schlechter Wirkungsgrad und (besonders bei Kurzwelle) die Verzerrungen durch selektiven Trägerschwund gegenüber, so dass in vielen Anwendungen nun abgewandelte Modulationsverfahren genutzt werden.

Modulation

Es gibt zwei Arten der Modulation:

• Mathematisch: Trägersignal mit Nutzsignal multiplizieren
• Praktische Realisierung: Trägersignal mit Nutzsignal addieren (überlagern) danach verzerren und filtern.

Mathematische Beschreibung

Nachfolgend werden sowohl die eigentliche Frequenz f als auch die Kreisfrequenz ω mit Frequenz bezeichnet. Dies ist möglich, da beide über einen konstanten Faktor 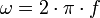$\omega=2 \cdot \pi \cdot f$ zusammenhängen. Trotzdem muss man beachten, dass beide immer noch zwei verschiedene Größen sind. Wenn Zahlen auftreten, wird das über die Einheiten ausgedrückt: [f] = Hz und [ω] = 1/s.

Abb. 1: Beispiel zur Amplitudenmodulation(m = 0,5)

Man erhält ein moduliertes Signal, wenn man zum Nutzsignal

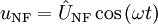$u_{\rm NF}=\hat U_{\rm NF}\cos{(\omega t)}$ (der Nullphasenwinkel wird als Null angenommen)

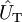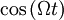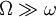einen Gleichanteil $\hat U_{\rm T}$ addiert und anschließend beides mit einer hochfrequenten Trägerschwingung $\displaystyle \cos{(\Omega t)}$ mit $\ \Omega \gg \omega$ multipliziert

$u_{\rm AM}=(\hat U_{\rm T}+\hat U_{\rm NF}\cos{(\omega t)})\cdot \cos{(\Omega t)}$

$u_{\rm AM}=\hat U_{\rm T}\cos{(\Omega t)}+\hat U_{\rm NF}\cos{(\omega t)}\cdot \cos{(\Omega t)}$

Mit Hilfe des Additionstheorems

$\cos \alpha \cos \beta = \frac{1}{2}(\cos {(\alpha -\beta )}+\cos{(\alpha +\beta)})$

erhält man:

$u_{\rm AM}=\hat U_{\rm T}\cos{(\Omega t)}+\frac{\hat U_{\rm NF}}{2}\left(\cos{((\Omega -\omega )t)}+\cos{((\Omega +\omega )t)}\right)$

Aus der Formel kann man das entstandene Frequenzspektrum ablesen. Das modulierte Signal enthält den Träger

$u_{\rm T}=\hat U_{\rm T}\cos{(\Omega t)}$

mit der Trägerfrequenz Ω und der Amplitude 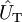$\hat U_{\rm T}$, sowie zwei Schwingungen mit den Seitenfrequenzen Ω − ω und Ω + ω mit jeweils der Amplitude 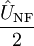$\frac{\hat U_{\rm NF}}{2}$. Diese einfachste Modulationsart der AM nennt man deshalb auch Zweiseitenbandmodulation (ZSB oder englisch DSB) mit Träger. Hier steckt die Information in den Seitenbändern, während der Träger selbst bei der Übertragung nur unnötigen Ballast darstellt. 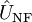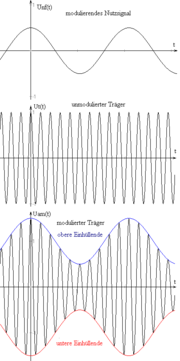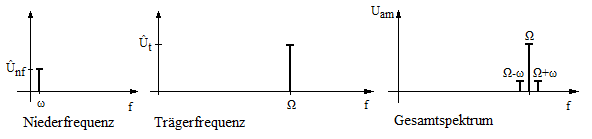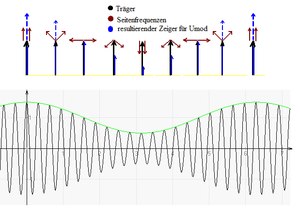Wenn sich die Amplitude $\hat U_{\rm NF}$ der modulierenden Schwingung ändert, ändert sich auch die Amplitude der Seitenfrequenzen. Wenn sich die Frequenz des modulierenden Signals ändert, ändern sich auch die Frequenzen der Seitenbänder.

In Abbildung 1 kann man unten neben dem modulierten Signal auch noch die beiden sogenannten Einhüllenden sehen. Diese dienen nur der Veranschaulichung, weil ihr Verlauf gleich dem modulierenden Nutzsignal ist. In Abbildung 2 sieht man die drei Spektren (von links) des modulierenden Nutzsignals, des unmodulierten Trägers und des modulierten Signals. Wie man erkennen kann, sind die Amplituden der informationstragenden Seitenbänder wesentlich kleiner als die des Trägers.

Abb. 2: Spektrum der Amplitudenmodulation; Modulationsgrad m = 0,5

Alternativ zur Berechnung des modulierten Signals im Zeitbereich kann dies auch über die Fourier-Transformation im Frequenzbereich geschehen. Die dazu inverse Fourier-Transformation führt wieder in den Zeitbereich.

Modulationsgrad

Abb. 3: Modulationsgrad und Modulationstrapez in drei Varianten

Mit dem Modulationsgrad m wird angegeben, wie stark das zu modulierende Nutzsignal die Amplitude des modulierten Signals beeinflusst.

$m = \frac{\hat U_{\rm NF}}{\hat U_{\rm T}} = \frac{U_{\rm AM_{\rm max}}-\hat U_{\rm T}}{\hat U_{\rm T}} = \frac{U_{\rm AM_{\rm max}}-U_{\rm AM_{\rm min}}}{U_{\rm AM_{\rm max}}+U_{\rm AM_{\rm min}}}$

Mit m ergibt sich für u_AM

$u_{\rm AM}=\hat U_{\rm T} \left(\cos{(\Omega t)}+\frac{m}{2}(\cos{((\Omega -\omega)t)}+\cos{((\Omega +\omega )t)})\right)$

Er muss größer als 0 und kleiner gleich 1 sein, um eine sinnvolle Modulation zu gewährleisten. Bei Null findet keine Modulation statt, es wird lediglich der unmodulierte Träger übertragen. Bei m > 1 findet eine Übermodulation statt, das entstandene Signal kann nicht mehr ohne Verzerrungen demoduliert werden. Deshalb wird oft die Amplitude des modulierenden Signals vorher begrenzt, um eine zu große Aussteuerung zu vermeiden.

Modulationstrapez

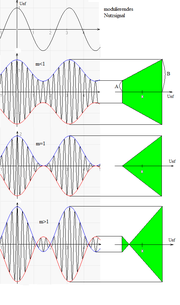
Beim Modulationstrapez wird die Amplitude des modulierten Signals (y-Achse) über der Amplitude des modulierenden Signals (x-Achse) aufgetragen. Bei sinusförmigen Signalen entsteht dabei ein Trapez. Je nachdem wie groß m ist, kann es wie ein normales Trapez (0 < m < 1) aussehen, wie ein Dreieck (m = 1) oder eine Fischform (m > 1) (siehe Abbildung 3). Aus dem Trapez lässt sich auch leicht die Formel für m bestimmen.

$m=\frac{B-A}{B+A}$

Wenn die Phase nicht konstant bleibt oder kein reines Sinussignal vorliegt, treten Verzerrungen des Modulationstrapezes auf oder es kann sich zu einem Zylinder wölben.

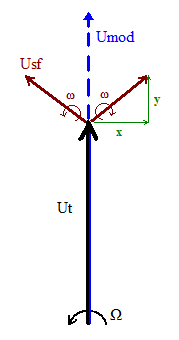
Zeigerdarstellung

In der Zeigerdarstellung werden die Modulationsanteile als Zeiger abgetragen. Auf dem starren Träger stehen die beiden Zeiger der Seitenfrequenzen und drehen sich mit ω in jeweils entgegengesetzte Richtung. Wie man in den Abbildungen 4 und 5 sehen kann, sind die x-Komponenten der Zeiger der Seitenfrequenzen stets entgegengesetzt, so dass sie sich bei der Addition aufheben. Es bleibt nur noch die Summe der y-Komponenten, die zur Trägeramplitude addiert (wenn negativ subtrahiert) wird. So ist die resultierende momentane Amplitude des modulierten Signals immer in gleicher Richtung (in Phase) mit der Trägeramplitude. Das ist charakteristisch für die Zweiseitenbandmodulation.

Abb. 4: Zeigerdarstellung der Amplitudenmodulation

Abb. 5: Zusammenhang zwischen Amplitude von Umod und Zeigerdarstellung

Bandbreite

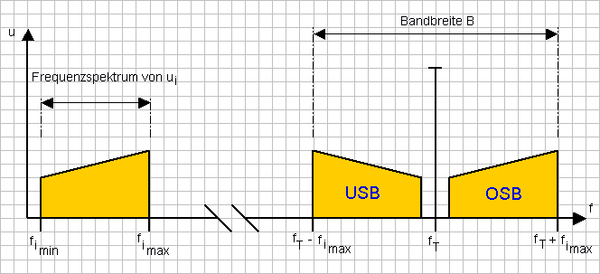
Das Beispiel war sehr einfach, um grundlegend die Modulation verstehen zu können. Praktisch wird dabei eine niedrige Frequenz, also zum Beispiel ein einziger Ton konstanter Stärke auf den Träger moduliert. In der Realität moduliert man wesentlich mehr aufeinanderfolgende Frequenzen auf den Träger. Diese Menge an Frequenzen nennt man Frequenzband f_B und somit die Bereiche, die nach der Modulation neben dem Träger entstehen, Seitenbänder. Es gibt ein oberes (OSB) und ein unteres (USB) Seitenband. Zusammen bilden sie die Bandbreite B.

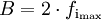$B = 2 \cdot f_{\rm i_{\rm max}}$ Gilt nur näherungsweise, da z.B. in UKW-Bereich(15Hz-15kHz) :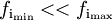 $f_{\rm i_{\rm min}} &amp;amp;lt;&amp;amp;lt; f_{\rm i_{\rm max}}$

Abb. 7: Amplitudenmodulation im Spektrum

Beim Rundfunk wird im AM-Bereich ein standardisiertes Frequenzband von 4,5 kHz Breite (von 0 Hz bis 4,5 kHz) übertragen, was zu einer Bandbreite B = 9 kHz führt.

Leistungsbetrachtung

Die eigentliche Nutzleistung steckt in den Seitenbändern, wobei in beiden Seitenbändern die gleiche Information steckt, was folglich bedeutet, dass ein Seitenband völlig überflüssig ist, wie auch der Träger. Daraus ergibt sich ein Wirkungsgrad η.

$\eta =\frac{P_{\rm SB}}{P_{\rm ges}}=\frac{m^2}{4+2m^2}$

mit

$P_{\rm ges} = P_T+2\ P_{\rm SB}$

$P_{\rm T} =\frac{{\hat U_{\rm T}}^2}{2R}$

$P_{\rm SB} = \frac{{\hat U_{\rm NF}}^2}{8R}$

R ist ein beliebiger Widerstand, auf den die Leistung bezogen wird. Je nachdem, wie nun m gewählt wird, beträgt η zwischen 0 % (m = 0) und 17 % (m = 1).

Praktische Realisierung der Modulation

Ausnutzung der nichtlinearen Kennlinie eines Bauteils

Abb. 8: Addition beziehungsweise Überlagerung von Trägersignal u_T und Informationssignal u_i zu u_T+i

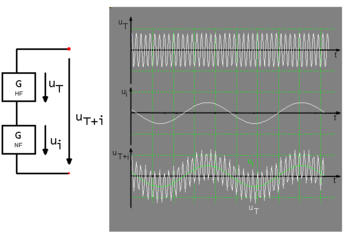
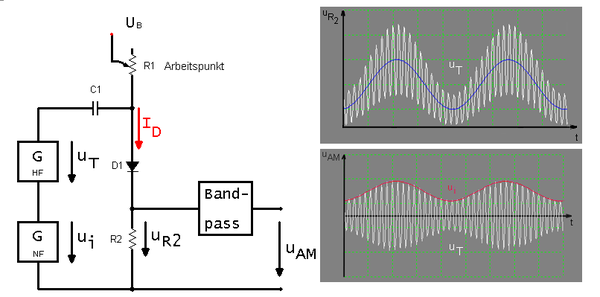
Bei diesem Verfahren wird ein nichtlineares Bauteil, gewöhnlich eine Diode, durch ein Signalgemisch ausgesteuert. Das Gemisch u_{T + i} ergibt sich durch Addition aus dem modulierenden Signal u_i und der Trägerschwingung u_T. Erzeugt werden diese Signale durch zwei Generatoren (HF-Oszillator und einen NF-Verstärker), die in Reihe geschaltet sind (Abb. 8).

In Abb. 9 ist die Schaltung des Modulators dargestellt. Um später ein einwandfreies AM-Signal zu erhalten, muss vorher der Arbeitspunkt der Diode mit R₁ so eingestellt werden, dass die Diode eben noch leitfähig ist (Schwellspannung). Das bedeutet, dass der Arbeitspunkt am unteren Ende der Kennlinie liegt. Es fließt daher ein geringer Diodenstrom I_D. C₁ dient zur Abblockung der Diodenvorspannung, damit diese nicht rückwärts in den HF-Generator fließt. Über C₁ liegt die Spannung u_{T + i} an der Diode an, wodurch der Arbeitspunkt im Takt von u_{T + i} an der gekrümmten Kennlinie hoch- und heruntergeschoben wird. Durch die Änderung des Arbeitspunktes ändert sich auch I_D. Die Änderung von I_D führt seinerseits nach dem Ohmschen Gesetz proportional zu einer Änderung des Spannungsabfalls u_R2 über R₂. u_R2 ist folglich eine Funktion von u_{T + i}, wobei die Funktion durch die Kennlinie der Diode festgelegt wird. Durch eine Taylorreihe, die nach dem quadratischen Glied abgebrochen wird

$P_{u_{R2}}(u_{T+i}) = u_{R2}(u_{T+i}=0) + \frac{\partial u_{R2}(u_{T+i}=0)}{\partial u_{T+i}} u_{T+i} + \frac{1}{2} \frac{\partial^2 u_{R2}(u_{T+i}=0)}{\partial u^2_{T+i}} u^2_{T+i}$

mit

$u_{T+i} = u_T + u_i = \hat U_{\rm T}\cos{(\Omega t)} + \hat U_{\rm NF}\cos{(\omega t)}$

und

$u_{R2} = R_2 \cdot I_D = R_2 \cdot I_S \left( e^{\frac{u_{T+i}}{n \cdot U_{Temp}}} - 1\right)$,

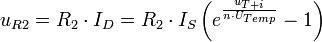kann die Funktion u_R2 angenähert werden. Mit den Faktoren

$\!\, u_{R2}(u_{T+i}=0) = 0$

$\frac{\partial u_{R2}(u_{T+i}=0)}{\partial u_{T+i}} = \frac{R_2 I_S}{n \cdot U_{Temp}}$

$\frac{\partial^2 u_{R2}(u_{T+i}=0)}{\partial u^2_{T+i}} = \frac{R_2 I_S}{(n \cdot U_{Temp})^2}$

ergibt sich die Näherung zu:

$\begin{align} P_{u_{R2}}(u_{T+i}) = &amp;amp;amp;\underline {\frac{R_2 I_S}{n \cdot U_{Temp}} \hat U_{\rm T}\cos{(\Omega t)}} + \frac{R_2 I_S}{n \cdot U_{Temp}} \hat U_{\rm NF}\cos{(\omega t)} \\ &amp;amp;amp;+ \frac{1}{4} \frac{R_2 I_S}{(n \cdot U_{Temp})^2} \left( \hat U^2_{\rm T} + \hat U^2_{\rm NF} + \hat U^2_{\rm T}\cos{(2\Omega t)} + \hat U^2_{\rm NF}\cos{(2\omega t)}\right) \\ &amp;amp;amp;+ \underline {\frac{1}{2} \frac{R_2 I_S}{(n \cdot U_{Temp})^2} \hat U^2_{\rm T} \hat U^2_{\rm NF} \left( \cos{((\Omega - \omega) t)} + \cos{((\Omega + \omega) t)}\right)} \end{align}$

Dieses Ergebnis enthält noch viele Frequenz- und Gleichanteile, die den gewünschten Verlauf verzerren. Auch der blaue Graph im u_R2 Diagramm zeigt dies deutlich. Der Gleichspannungsanteil kommt daher, dass durch die Arbeitspunkteinstellung immer ein geringer Diodengleichstrom I_D fließt, welcher einen Gleichspannungsabfall an R₂ erzeugt. Um ein AM-Signal zu erhalten, muss u_R2 noch auf einen Bandpass gegeben werden, welcher die Gleichspannung und die durch die Modulation hervorgerufenen unerwünschten Frequenzanteile abblockt. Die gesuchten Anteile sind in der genäherten Formel unterstrichen dargestellt und bleiben nach der Filterung übrig:

$u_{AM} = \frac{R_2 I_S}{n \cdot U_{Temp}} \hat U_{\rm T}\cos{(\Omega t)} + \frac{1}{2} \frac{R_2 I_S}{(n \cdot U_{Temp})^2} \hat U^2_{\rm T} \hat U^2_{\rm NF} \left( \cos{((\Omega - \omega) t)} + \cos{((\Omega + \omega) t)}\right)$

Das u_AM-Diagramm zeigt das fertige AM-Signal. Rot gekennzeichnet ist das modulierende Signal u_i, welches die Amplitude des modulierten Signals beeinflusst.

Abb. 9: Einfacher Diodenmodulator

Multiplikative Modulation

Abb. 10: Sender mit Amplitudenmodulation

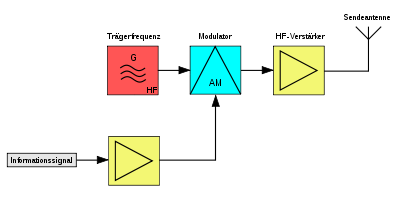
Das Nutzsignal ist in der Regel ein Frequenzgemisch (z. B. Sprache). Als NF-Quelle kann z. B. ein Mikrofon dienen. Die Trägerfrequenz selber wird mit Hilfe eines HF-Generators oder auch Oszillators erzeugt.

Die eigentliche Modulation geschieht im Modulator, wie in der Mathematischen Beschreibung dargestellt, durch Multiplikation des modulierenden Signals und eines Gleichanteils (sowie Verzerrungen aufgrund Nichtlinearitäten) mit der Trägerschwingung. Elektronisch kann man eine 2-Quadranten-Multiplikation beispielsweise mit einem Differenzverstärker realisieren. (Beim Differenzverstärker-Beispiel bekommt Transistor Q₁ HF und die Stromquelle Q₃ bekommt NF).

Wenn 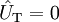$\hat U_{\rm T} = 0$ ist, kann ein negativer Wert des modulierenden Signals (u_NF < 0) den Träger invertieren (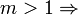$m&amp;amp;gt;1 \Rightarrow$ Übermodulation). Abgesehen davon funktioniert ein Differenzverstärker dann nicht (Betrieb nur in 2 Quadranten möglich). Also ist 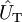$\hat U_{\rm T}$ so zu wählen, dass 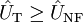$\hat U_{\rm T} \ge \hat U_{\rm NF}$ gilt.

Das modulierte Signal gelangt schließlich nach dem HF-Verstärker zur Antenne und wird als Elektromagnetische Welle zum Empfänger übertragen.

Weitere Arten der Amplitudenmodulation

Bandbreiten- oder leistungsbegrenzende Modulationsvarianten

• Amplitudenmodulation mit unterdrücktem Träger (DSBSC, double side band supressed carrier)
• Einseitenbandmodulation (SSB, single side band)
• Restseitenbandmodulation

Verfahren mit geringer Anfälligkeit gegen Störungen oder größerer Nutzung des Spektrums:

• Quadraturamplitudenmodulation QAM
• dynamische Amplitudenmodulation
• Pulsamplitudenmodulation (PAM)

Demodulation

Kohärente Demodulation (Synchrondemodulation)

Beim Empfänger existiert ein lokaler Träger, der in Phase zum Träger des empfangenen Signals ist. Beide sind folglich zueinander synchron und damit kohärent. Die Erzeugung dieses lokalen Trägers ist technisch sehr aufwendig, dafür ist die mathematische Beschreibung der Demodulation recht einfach. Zunächst wird das empfangene Signal, bestehend aus den beiden Seitenfrequenzen und dem Träger, mit dem lokalen Träger multipliziert:

$\begin{align} u_{\rm DAM} &amp;amp;amp;= u_{\rm AM} \cdot \cos{(\Omega t)}\\ &amp;amp;amp;= \left(\hat U_{\rm T}\cos{(\Omega t)}+\frac{\hat U_{\rm NF}}{2}\left(\cos{((\Omega -\omega )t)}+\cos{((\Omega +\omega )t)}\right)\right) \cdot \cos{(\Omega t)}\\ &amp;amp;amp;= \hat U_{\rm T}\cos^2{(\Omega t)}+\frac{\hat U_{\rm NF}}{2}\left(\cos{((\Omega -\omega )t)}\cdot \cos{(\Omega t)} + \cos{((\Omega +\omega )t)} \cdot \cos{(\Omega t)}\right) \end{align}$

Mit Hilfe der Additionstheoreme

$\cos \alpha \cos \beta = \frac{1}{2}(\cos {(\alpha -\beta )}+\cos{(\alpha +\beta)})$

$\cos^2 \alpha = \frac{1}{2} \left(1 + \cos{(2\alpha)} \right)$

erhält man:

$\begin{align} u_{\rm DAM} = \frac{\hat U_{\rm T}}{2} \left(1 + \cos {(2\Omega t)} \right) +\frac{\hat U_{\rm NF}}{4}\left( \cos{(-\omega t)}+\cos{((2\Omega -\omega )t)} +\cos{(\omega t)}+\cos{((2\Omega +\omega )t)} \right) \end{align}$

Anschließend werden die unerwünschten hohen Frequenzanteile (2Ω) mit einem Tiefpass und der Gleichanteil mit einem Hochpass herausgefiltert, wodurch nur noch das gesuchte Nutzsignal mit halber Amplitude übrig bleibt:

$u_{\rm TP} = \frac{\hat U_{\rm NF}}{4}\left(\cos{(-\omega t)}+\cos{(\omega t)}\right)=\frac{\hat U_{\rm NF}}{2}\cos{(\omega t)}$

Inkohärente Demodulation (Hüllkurvendemodulation)

Ohne die aufwendige Erzeugung eines lokalen Trägers kommt diese einfachste Form der Demodulation aus. Hier wird das gesuchte Frequenzband mit einem Bandpass herausgefiltert, anschließend mit einer Diode gleichgerichtet und zum Schluss mit einem Tiefpass geglättet. Der enthaltene Gleichanteil wird gegebenenfalls mit einem Hochpass entfernt.

$u_{\rm DAM} = \left| u_{\rm AM} \right|$

Auf Grund der Einfachheit dieses Verfahrens ist das empfangene Signal häufig durch Verzerrungen gestört. Praktische Umsetzungen dieses Verfahrens stellen der Hüllkurvendemodulator und der Detektorempfänger dar. Durch die Einweggleichrichtung geht die Hälfte des Signals verloren. Eine Zweiwegegleichrichtung mit vier Dioden ist allerdings unüblich.

Siehe auch:

• Gittergleichrichtung
• Anodengleichrichtung
• Kathodengleichrichtung

Überlagerungsempfänger

Die heute verbreitetste Form der Demodulation. Siehe dazu Überlagerungsempfänger.

Mehrstufige Multiplikative Demodulation

Zunächst wird mit einem auf die Trägerfrequenz f_T abstimmbaren leicht gedämpften Schwingkreis eine schmalbandige Verstärkung (Bandpass) des gewünschten Frequenzbereichs (f_T − f_i max bis f_T + f_i max) durchgeführt. Danach wird, je nach zur Verfügung stehender Technologie, die Modulation zu niedrigeren Frequenzen in n Stufen durchgeführt. Also je Stufe ein Modulator gefolgt von einem Tiefpass. Der Modulator selbst ist wie beim Sender ein Multiplizierer. In diesem Beispiel gibt es zur Vereinfachung nur einen (n = 1) Modulator. Die für den Modulator erforderliche Trägerfrequenz im Empfänger f_Te sollte möglichst gut der Trägerfrequenz des Senders f_T entsprechen, da ansonsten eine Schwebung entsteht. Die Nachregelung von f_Te erfolgt heutzutage über eine PLL (Phase locked loop).

Ergebnis des Sender: f_m1 = 220 kHz und f_m2 = −240 kHz; f_T = 230 kHz
(Phase über Vorzeichen dargestellt)

Im Empfänger unter Voraussetzung f_T = f_Te:

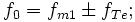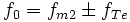$f_0 = f_{m1} \pm f_{Te};$ und $f_0 = f_{m2} \pm f_{Te}$ (Phase und Amplitude weggelassen)

woraus sich mit obigen Angaben die Frequenzen ergeben: −10 kHz; 450 kHz; −10 kHz; −470 kHz

Alle Frequenzen oberhalb von 10 kHz lassen sich nun einfach über einen Tiefpass ausfiltern.

Im Realfall ist es kaum möglich, die Trägerfrequenz des Senders hinreichend genau zu treffen. Um eine Vorstellung von der erforderlichen Genauigkeit zu bekommen, hier ein Beispiel: Eine Schwebung von 50 Hz entspricht einer Frequenzabweichung von 0,02 % bezogen auf 230 kHz. Um möglichst vielen Problemen der Analogtechnik (muss justiert werden, elektronische Bauteile altern) aus dem Weg zu gehen und Platzbedarf zu minimieren, wird zunehmend auf digitale Signalverarbeitung gesetzt. Im Prinzip wird mit einem schnellen Analog-Digital-Umsetzer direkt das Empfangssignal in Sinus- und Cosinus-Anteil digitalisiert. Der Rest wird rechnerisch vom Signalprozessor geleistet.

Kurzbezeichnungen

• A1 – Amplitudentastung
• A2 – tönende Telegrafie
• A3 – amplitudenmodulierte Übertragung analoger Signale (zum Beispiel von Sprache und Musik)

Siehe auch

Weblinks

• Übersicht Modulationsverfahren (PDF)
• Übersicht Modulationsverfahren (PDF)
• Amplitudenmodulation (PDF)
• Modulation und Rauschen (PDF)

Technische Modulationsverfahren

Übersicht: Modulator 

Analoge Modulationsverfahren: AM | SSB | DSBSC | SSBSC | FM | PM | VM 

Digitale Modulationsverfahren: ASK | FSK | GFSK | QPSK | QAM | OFDM | DMT | TCM 

Pulsmodulationsverfahren: PWM | PAM | PFM | PPM | PCM 

Spezielle Modulationsverfahren: FHSS | DSSS 

Optische Modulationsverfahren: Allgemein | Polarisationsmodulatoren | Akustooptischer Modulator | Photoelastischer Modulator