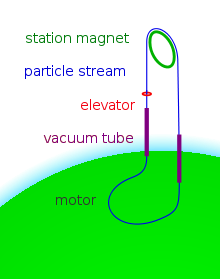
Weltraumturm

Ein Weltraumturm ist ein Turm auf der Erde oder einem anderen Himmelskörper, der so hoch ist, dass von seiner Spitze der Orbit vergleichsweise einfach erreicht werden kann. Bisher ist kein solcher Turm errichtet worden. Auf der Erde muss die Spitze des Turmes mindestens die Kármán-Linie in 100 km Höhe erreichen, um als Weltraumturm zu gelten. Im Prinzip kann sie die geostationäre Bahn erreichen.

Allgemeines

Auf der Erde ist das Besondere an einem Weltraumturm seine Höhe von mindestens 100 km. Dies stellt besondere Herausforderungen an die Konstruktion. Der Nutzen eines solchen Turms stellt die Vereinfachung dar, den Weltraum zu erreichen. Anstelle von chemischen Raketen kann ein Aufzug benutzt werden, um Nutzlasten in den Weltraum zu transportieren. Zum Anpassen der Bahngeschwindigkeit Delta-v kann eine kleine Rakete eingesetzt werden. Ob ein Weltraumturm ökonomischer ist als die chemischen Raketen, ist noch nicht im Detail untersucht worden und hängt stark vom Transportvolumen bzw. -gewicht ab.

Natürlich sind auch Kombinationen von Weltraumturm und Weltraumlift per Kabel möglich. Die Spitze des Turms kann als Ankerpunkt für ein Weltraumkabel dienen. Wenn wir mehrere Weltraumtürme in einer Reihe errichten, dann können wir sie für einen Raumsteg^[1] nutzen^[2].

Für einen Turm am Äquator, der die geostationäre Bahn erreicht, ist keine Anpassung der Bahngeschwindigkeit notwendig. Bei kleineren Türmen muss die Geschwindigkeit einer Nutzlast erhöht werden, um einen stabilen Orbit zu erreichen. Die Geschwindigkeit kann ganz oder teilweise vom Aufzug mitgegeben werden. Die Nutzlast kann auch zunächst etwas nach unten fallen, bevor die Bahngeschwindigkeit erreicht ist. Deswegen braucht man keine so starken Motoren, wie bei einem senkrechten Start vom Boden (hier muss direkt die Erdbeschleunigung überwunden werden – schon bei einem horizontalen Start kann man bereits schwächere Motoren einsetzen).

Vorteile gegenüber einem Weltraumlift per Kabel

• Der Weltraumturm kann mit der Technik des Jahres 2000 erbaut werden. Er benötigt keine exotischen Materialien.
• Der Weltraumturm wird vom Boden nach oben errichtet und nicht von der geostationären Bahn aus nach unten und oben zugleich.
• Der Weltraumturm kann im Prinzip an jedem Punkt auf der Erde errichtet werden und nicht nur am Äquator.
• Der Weltraumturm kann auch auf Himmelskörpern errichtet werden, die nicht oder nur sehr langsam rotieren, z.B. Mond, Venus.
• Der Weltraumturm ist nicht so stark durch Weltraummüll gefährdet, da er nicht so hoch ist, wie das Kabel des Weltraumlifts lang ist.

Nachteile gegenüber einem Weltraumlift per Kabel

• Der Weltraumturm kann nicht über die geostationäre Bahn (als Abstand von der Rotationsachse betrachtet) hinaus reichen. Dann überwiegt an der Spitze die Fliehkraft die Schwerkraft. Diese Zugspannung kann nicht (leicht) ausgeglichen werden.

Geschichte

Die Idee entstammt einer Diskussion von Marvin Minsky vom MIT und John McCarthy und Hans Moravec von der Stanford University mit Roderick Hyde und Lowell Wood vom Lawrence Livermore National Laboratory in den 1980ern. Hier wurden Stationen in 2000 km Höhe vorgeschlagen, die sich nicht in einem stabilen Orbit befinden, sondern durch einen Massefluss stabilisiert werden. So können die Stationen ständig über einen festen Punkt der Erde stehen während sich der Massefluss schneller als mit Orbitalgeschwindigkeit bewegt.

Der Physiker und Science-Fiction-Autor Robert L. Forward hat diese Idee zum Weltraumturm weiterentwickelt.^[3]

Konstruktion

Zur Konstruktion hoher Türme sind drei verschiedene Techniken vorstellbar: Zum einen statische Türme, bei denen das Gewicht als Druck auf das Konstruktionsmaterial wirkt. Bei hohen Türmen ist viel Material notwendig. Diese Methode wird bis heute (2009) bei allen Türmen, die jedoch alle weniger als 1 km hoch sind und somit keine Weltraumtürme sind, verwendet. Zum zweiten sind Türme mit dynamischer Kompression möglich. Diese Technik wird zur Zeit (2009) noch nicht eingesetzt, obwohl sie technisch ohne weiteres möglich wäre. Details siehe Dynamische Türme. Zum dritten sind schwebende Türme möglich. Dabei ist das Baumaterial derart leicht, dass der atmosphärische Auftrieb das Turmgewicht trägt.

Unabhängig von der Art des Turms wirken auf ihn die Schwerkraft und Fliehkraft (falls der Himmelskörper rotiert und der Turm nicht auf einem Pol steht) sowie Auftrieb, falls der Himmelskörper eine Atmosphäre hat. Ein Turm am Äquator oder an den Polen kann genau senkrecht errichtet werden. Falls der Turm an einem anderen Ort errichtet wird, wird er leicht zur Äquatorialebene gekrümmt sein, um die Veränderung der beiden Kräfte auszutarieren. Weil der Turm nicht exakt gerade ist, ist seine Länge durch die Bogenlänge zu beschreiben und nicht durch die Höhe. An den Polen ist die Höhe des Weltraumturms nicht durch die Fliehkraft beschränkt. (Im Prinzip sind an den Polen der Erde Türme der Höhe 50.000 km und mehr möglich. Dann wirken auf den Turm die Gezeitenkräfte von Sonne und Mond (etc.) sowie die Präzession der Erde, so dass die Höhe nicht unbegrenzt ist.)

Statische Türme

Bei statischen Türmen wird ein Material, das gut Druckkräfte aushält, eingesetzt, um das Gewicht der Turmspitze zu tragen. Als Material wird vielfach Beton eingesetzt. Da jedes Material nur begrenzt Druckkräfte aufnehmen kann, ohne zerstört zu werden, muss man bei hohen Türmen an der Turmbasis eine große Grundfläche vorsehen. Der Turm verjüngt sich (etwa exponentiell) mit zunehmender Höhe, damit nirgends der Druck den Grenzdruck des Materials übersteigt. Die Größe der Fläche sowie die Verjüngung lassen sich mit Hilfe von Differenzialgleichungen ermitteln. Wie heute üblich, kann man einen solchen Turm vom Fundament nach oben errichten.

Herleitung des Flächenbedarfs

Im Gleichgewicht müssen sich alle (infinitesimalen) Kräfte aufheben, also gelten:

0 = dF_M + dF_T,γ + dF_T,ω

mit

s		Bogenlänge in Bezug auf den Weltraumturm
FM(s)	= pA(s)	Schwerelast des Weltraumturms
dFT,γ(s)	$= - \gamma \frac{M}{r^2(s)} \rho_T(s) \mathrm ds \begin{pmatrix} \sin\varphi(s)\\ \cos\varphi(s) \end{pmatrix}$	Schwerkraft auf das infinetismale Turmelement an der Stelle s
dFT,ω(s)	$= \omega^2 r(s) \rho_T(s) \mathrm ds { 1\choose 0}$	Fliehkraft auf das Turmelement
x(s)	$= \begin{pmatrix}x_1(s)\\x_2(s)\end{pmatrix}$	Position des Turms bei seiner Länge s
ds	$= \sqrt{\mathrm dx_1^2 + \mathrm dx_2^2}$	Berechnung der infinitesimalen Bogenlänge
φ(s)	$= \arctan\frac{x_1(s)}{x_2(s)}$	Winkel zur Rotationsachse
r(s)	$= \sqrt{x_1^2(s) + x_2^2(s)}$	Abstand zum Mittelpunkt des Himmelskörpers
γ	$= -6{,}67259(85)\cdot 10^{11} \mathrm{m^3kg^{-1}s^{-1}}$	universelle Gravitationskonstante
ρT(s)	= ρ0A(s)	Dichte des Turms pro Länge (Masse eines Turmstücks / Bogenlänge dieses Stücks)
ρ0		Dichte des Turms pro Volumen
p		Maximale Druckbelastung des Materials
A(s)		Fläche des Turms bei der Länge s
dx	$= \frac{F_M(s)}{|F_M(s)|} \mathrm ds$
M	$= 5{,}97370(76)\cdot 10^{24}\mathrm{kg}$	Masse des Himmelskörpers, hier der Erde
r0	= 6.378,140km	Äquatorialradius des Himmelskörpers, hier der Erde
ω	$= 2\pi(24\cdot60\cdot60)\mathrm s^{-1}$	Winkelgeschwindigkeit des Himmelskörpers, hier der Erde

Diese Gleichungen lassen sich numerisch lösen um die Grundfläche A(0) und die Verjüngung A(s) zu erhalten. Als entscheidende Materialeigenschaft ergibt sich aus den ersten Gleichungen das Verhältnis Druckfestigkeit je Dichte p / ρ₀.

Dies Verhältnis legt im Wesentlichen die Grenze für statische Türme fest. Heutige Materialien haben Stärken von höchstens 10MN / m² / (kg / m³).^[4]

Ohne Rotation (ω = 0) kann man die Gleichungen analytisch löschen. Es ergibt sich

$A(s) = A(0) \cdot \exp \left(-g r_0^2 \frac{\rho}{p} \frac{s}{r_0(r_0-s)} \right)$

≈$A(0) \cdot \exp \left(-g \frac{\rho}{p} s \right)$ ist mit $g=\gamma M/r_0^2$.

Dann ist s gleich der Höhe.

Einfache Beispielrechnung

Für Beton ist $\rho_0 = 2.600\, \mathrm{kg m^{-3}}$ mit $p = 100\, \mathrm{N\cdot mm^{-2}}$ möglich. Bei einer Grundfläche A(0) von $10.000\, \mathrm m^2 = (100\, \mathrm m)^2$ erhält man in 100 km Höhe eine Fläche $A(100\,km) = (0,37\,\mathrm {mm})^2$. Die Spitze ist also eine ausgesprochen dünne Betonnadel. Falls man in der Höhe eine Fläche von $1\,\mathrm m^2$ benötigt, ist am Boden eine Fläche von mehr als $(270\,\mathrm{km})^2$ notwendig. Das ist nicht praktikabel. (Das Volumen des Turms betrüge über 280 Billionen m³, = $(65\,\mathrm{km})^3$. Dazu wäre etwa das 30.000-fache der weltweiten Jahresproduktion von Zement, vgl. Liste der größten Zementhersteller, nötig.)

Auf Himmelskörpern mit kleiner Masse wie zum Beispiel Deimos ist ein statischer Weltraumturm sehr wohl möglich.

Dynamische Türme

Bei dynamischen Türmen wird die Gewichtslast durch einen Massefluss übertragen. Der Massefluss besteht aus bewegten Teilchen, die als solche eine Masse, genauer einen Impuls, haben. Durch Abbremsen, Beschleunigen oder Umlenken wird vom Massefluss ein Impuls auf die umgebene Konstruktion übertragen. Dieser übertragene Impuls kann die Schwerebeschleunigung der Konstruktion oder andere Druckkräfte ausgleichen. Auch dieser Turm kann vom Fundament nach oben errichtet werden. Dabei ist die Verlängerung der Vakuumröhre am schwierigsten. Die Spitze zum Umlenken des Massefluss kann schon zu Beginn errichtet werden und mit dem Wachsen des Turms nach oben wandern.

Anschauliche Beschreibung

Zur Anschauung mag ein Wasserstrahl dienen, der aus einem Gartenschlauch hervorschießt. Ignoriert man hier die Luftreibung dann stellt man fest, dass sich das Wasser auf einer Parabelbahn bewegt. Wird der Wasserdruck erhöht, wird die Parabel steiler und schmaler. Richtet man den Gartenschlauch nahezu senkrecht nach oben, erhält man eine hohe und enge Parabel. Bei hinreichend großem Druck erreicht das Wasser theoretisch den Weltraum und fällt dann wieder zurück. (Bei noch größerem Druck verschwindet es in ihm, d.h. es erreicht Fluchtgeschwindigkeit und unterliegt in der Regel zunehmend der Schwerkraft anderer Himmelskörper.)

Wird der Schlauch im obigen Beispiel ruhig gehalten, kann auf der Spitze der Parabel ein Ball gesetzt werden. Das Gewicht des Balls drückt auf das hochströmende Wasser, so dass es gebremst wird und früher wieder zurückfällt. Es stellt sich jedoch ein Gleichgewicht ein, bei dem der Ball vom Wasser in großer Höhe getragen wird.

Damit die Luftreibung nicht stört, kann man ein Rohr als Hülle um den Wasserstrahl bauen. Aus dem Rohr kann man die Luft hinauspumpen, so dass man den Strahl durch die Atmosphäre leiten kann, ohne störende Luftreibung. Dann muss erreicht werden, dass das Rohr ähnlich wie der Ball von dem Strahl getragen wird.

Diesem Prinzip liegt der dynamische Weltraumturm zugrunde.

Beispielhafter Weltraumturm

Hyde Design;gelb - Vakuumröhre; rot - Aufzug; blau - Turm ohne Hülle; grün - Umlenkmagnet in der Spitze; schwarz - Beschleunigerring für den Massefluss

Für den Weltraumturm wird im Wesentlichen ein zirkulierender Massefluss eingesetzt, zum Beispiel aus Eisenstücken. Zunächst steigen diese mit hoher Geschwindigkeit auf. Dabei werden sie von der Konstruktion elektromagnetisch leicht abgebremst und generieren dabei elektrischen Strom. In seiner Spitze werden die Eisenstücke magnetisch umgelenkt, wodurch sie die Spitze tragen. Bei ihrer Bewegung abwärts werden sie mit dem elektrischen Strom, der bei der Bewegung aufwärts entstand, elektromagnetisch mit einem Linearmotor beschleunigt. Im Fundament wird der Massefluss zunächst in die Horizontale abgelenkt. In der Horizontalen wird er zum Turm zurück umgelenkt, um danach wieder in die aufstrebende Vertikale gelenkt zu werden, so dass der Kreis sich schließt.

Bei diesem Zyklus wird keine Energie benötigt, abgesehen vom Ausgleich von Reibung und Ineffektivitäten. Um die Reibung zu vermindern, bewegt sich der Massefluss durch ein evakuiertes Rohr. Für die Elektromagnete können Supraleiter eingesetzt werden.

Die Last des Turms wird auf das Fundament übertragen, während der Massefluss in die Horizontale bzw. Vertikale umgelenkt wird. Weil der Massefluss auf einem Kreisbogen umgelenkt wird, können heutige Materialien die Last tragen.

Als Massestrom eignen sich im Prinzip Kabel, Materiestücke, Plasma, Elementarteilchen und Photonen. Die Bestandteile müssen jedoch effizient umgelenkt und auf ihrer Bahn gehalten werden können. Obwohl Photonen die Ruhemasse Null besitzen, eignen sie sich doch, da sie einen Impuls übertragen. Dies liegt auch den Sonnensegeln zugrunde. Technisch wäre ein Photonenstrom eine große Herausforderung, da der Photonenstrom sehr intensiv sein muss und nahezu perfekte Spiegel benötigt werden.

Die Geschwindigkeit v(s) des Masseflusses in Abhängigkeit von der Bogenlänge s des Weltraumturms lässt sich wieder durch Differentialgleichungen analysieren.

Herleitung der Geschwindigkeit des Masseflusses

Im Gleichgewicht müssen sich alle (infinitesimalen) Kräfte aufheben, also gelten:

0 = dF_T,γ(s) + dF_T,ω(s) + dF_F,γ(s) + dF_F,ω(s) + dF_F(s)

mit

s		Bogenlänge in Bezug auf den Weltraumturm
dFF(s)	= − ρF(s)dsa(s)	Beschleunigungskraft des Masseflusses
dFT,γ(s)	$= - \gamma \frac{M}{r^2(s)} \rho_T(s) \mathrm ds { {\sin\varphi(s)} \choose {\cos\varphi(s)} }$	Schwerkraft auf das infinetismale Turmelement an der Stelle s
dFT,ω(s)	$= \omega^2 r(s) \rho_T(s) \mathrm ds { 1\choose 0}$	Fliehkraft auf das Turmelement
dFF,γ(s)	$= - \gamma \frac{M}{r^2(s)} \rho_F(s) \mathrm ds {\sin\varphi(s)\choose \cos\varphi(s)}$	Schwerkraft auf das infinetismale Stück des Massesflusses an der Stelle s
dFF,ω(s)	$= \omega^2 r(s) \rho_F(s) \mathrm ds {1\choose 0}$	Fliehkraft auf den Massefluss
x(s)	$= \begin{pmatrix}x_1(s)\\x_2(s)\end{pmatrix}$	Position des Turms bei seiner Länge s
ds	$= \sqrt{\mathrm dx_1^2 + \mathrm dx_2^2}$	Berechnung der infinitesimalen Bogenlänge
φ(s)	$= \arctan\frac{x_1(s)}{x_2(s)}$	Winkel zur Rotationsachse
r(s)	$= \sqrt{x_1^2(s) + x_2^2(s)}$	Abstand zum Mittelpunkt des Himmelskörpers
γ	$= -6{,}67259(85)\cdot 10^{11} m^3 \cdot\mathrm{ kg^{-1} \cdot s^{-1}}$	universelle Gravitationskonstante
ρT(s)		Dichte des Turms pro Länge
ρF(s)	$= \rho_F(0)\frac{|v(0)|}{|v(s)}$	Dichte des Massefluss pro Länge
dx	$= \frac{v(s)}{|v(s)|} \mathrm ds$
dv	$= \frac{a(s)}{|v(s)|} \mathrm ds$
M	$= 5{,}97370(76)\cdot 10^{24} \mathrm{kg}$	Masse des Himmelskörpers, hier der Erde
r0	= 6.378,140km	Äquatorialradius des Himmelskörpers, hier der Erde
ω	$= 2\pi(24\cdot60\cdot60)\mathrm s^{-1}$	Winkelgeschwindigkeit des Himmelskörpers, hier der Erde

Einfaches Beispiel

Wenn man das numerisch für ρ_T = 10kg / m und ρ_F = 1kg / m löst, ist für einen Turm am Äquator mit Höhe 100 km eine Geschwindigkeit des Massestroms am Boden von 1,8km / s ausreichend. Im Fundament kann man diesen Massestrom auf Kreisbahnen passend umlenken. Bei einem Kreis mit Radius 10 m wirkt durch die Zentrifugalkraft pro Meter des Kreisbogens eine Kraft von 324 kN. Diese Last kann ein 1 cm breiter Betonstreifen tragen und auf eine größere Bodenfläche übertragen.

Schwebende Türme

Im Prinzip sind hierfür Ballons übereinander zu stapeln. Der Höhenrekord für Ballons liegt bei 51,8 km (1972; Stand 1991). Das genügt auf der Erde nicht für einen Weltraumturm. Auf anderen Himmelskörpern könnte es genügen. Alternativ kann ein solcher Turm den unteren Abschnitt für weitere Abschnitte mit anderen Techniken bieten (dynamischer Turm oder Weltraumkabel).

Pneumatische Türme

Bei pneumatischen Türmen trägt ein Gas im Inneren den Turm. Das Gas kann Luft sein oder ein leichteres Gas, zum Beispiel Wasserstoff oder Helium. Die Gewichtslast der Nutzlast und der Turmhülle und des Turmgas selber erzeugen Druck auf das Gas. Da dieser Druck den Umgebungsdruck übersteigt, muss das Turmgas durch eine Hülle festgehalten werde. Diese Hülle steht unter Spannung.^[5][6].

Bei den meisten heute (2010) bekannten Materialien ist die maximale Zugspannung größer als die maximale Druckbelastung.^[5] Durch den pneumatischen Turm wird die bessere Zugeigenschaft für Türme genutzt, die auf Kompression beruhen. Weiter kann ein leichtes Traggas Auftrieb beisteuern. Mit heutigen (2010) Materialien sind Höhen von 10 km bis 200 km möglich.

Variationen der dynamischen Kompression

Die Methode der dynamischen Kompression, diese liegt dem Massestrom zu Grunde, lässt viele Variationen zu:

• Besonders hohe Falltürme oder Sendetürme.
• Besonders lange Brücken, z.B. von Europa bis Amerika. Hier beginnt der „Turm“ nicht senkrecht sondern nahezu horizontal.
• Stationäre Weltraumstationen in geringer Höhe (z.B. 100 km). Ein Massestrom im Orbit kann eine oder mehrere Weltraumstationen stützen, so dass sie über einen fixen Ort der Erdoberfläche schweben. Dazu muss der Massestrom schneller sein als die Bahngeschwindigkeit für einen gewöhnlichen Orbit, denn er hat die Stationen zu tragen.

Einzelnachweise

1. ↑ The Space Pier. Abgerufen am 18. Juli 2010. 
2. ↑ Proposed Free Standing Inflatable Tower to Reach 20 to 200 kilometers. Abgerufen am 18. Juli 2010. 
3. ↑ Robert L. Forward: Beanstalks. In: Indistinguishable From Magic, S. 79, Baen 1995, ISBN 0-671-87686-4
4. ↑ Paul Birch: Dynamic Compression Members. In: Journal of the British Interplanetary Society Vol. 42. 1989, S. 501-508, abgerufen am 29. November 2008 (GIF/ZIP (1,2 MB), englisch). 
5. ↑ ^{a b} Geoffrey A. Landis, Craig Cafarelli: THE TSIOLKOVSKI TOWER RE-EXAMINED, Journal of The British Interplanetary Society, Vol 52, S. 175-180, 1999.
6. ↑ B. M. Quine, R. K. Seth, Z. H. Zhu: A free-standing space elevator structure: a practical alternative to the space tether. Abgerufen am 4. September 2009 (pdf, englisch).