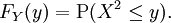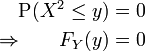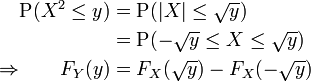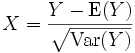- Zufallsgrösse
-
Eine Zufallsvariable oder Zufallsgröße (selten stochastische Variable oder stochastische Größe) ist ein Begriff aus dem mathematischen Teilgebiet Stochastik. Man bezeichnet damit eine Funktion[1], die den Ergebnissen eines Zufallsexperiments Werte (so genannte Realisationen) zuordnet.
Zum Beispiel kann das Zufallsexperiment des Münzwurfs als Zufallsvariable X modelliert werden. X bildet die Menge der Wurfergebnisse {Kopf,Zahl} auf die Menge der Realisationen {0,1} ab:
Die Bedeutung der Zufallsvariable liegt darin, dass durch sie die Verbindung zwischen dem Resultat eines Zufallsexperiments und seiner mathematischen Darstellung (Realisation) hergestellt wird. Auch lassen sich Funktionen von Realisationen des Experiments durch Zufallsvariable beschreiben.
Betrachtet man das zweimalige Werfen einer Münze und bezeichnet das Ergebnis mit
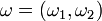 , so lassen sich beispielsweise folgende Zufallsvariable untersuchen:
, so lassen sich beispielsweise folgende Zufallsvariable untersuchen: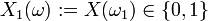 als Ergebnis des ersten Wurfes,
als Ergebnis des ersten Wurfes,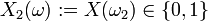 als Ergebnis des zweiten Wurfes,
als Ergebnis des zweiten Wurfes,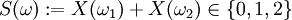 als Summe der zwei Ergebnisse.
als Summe der zwei Ergebnisse.
Zufallsvariable selbst werden üblicherweise mit einem Großbuchstaben bezeichnet (hier X1,X2,S), während man für die Realisationen die entsprechenden Kleinbuchstaben verwendet (so beispielsweise für
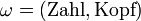 die Realisationen x1 = 1, x2 = 0, s = 1).
die Realisationen x1 = 1, x2 = 0, s = 1).Während früher der Begriff Zufallsgröße (manchmal auch Zufallsveränderliche) der übliche deutsche Begriff war, hat sich heute (ausgehend vom englischen random variable) der etwas irreführende Begriff Zufallsvariable durchgesetzt. Zufallsvariable sind jedoch Funktionen und dürfen nicht mit den Variablen verwechselt werden, die üblicherweise in der Mathematik eingesetzt werden.
Inhaltsverzeichnis
Definition
Als Zufallsvariable bezeichnet man eine messbare Funktion von einem Wahrscheinlichkeitsraum in einen Messraum.
Eine formale mathematische Definition lässt sich wie folgt geben:[2]
- Es seien (Ω,Σ,P) ein Wahrscheinlichkeitsraum und (Ω',Σ') ein Messraum. Eine (Σ,Σ')-messbare Funktion
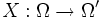 heißt dann eine Ω'-Zufallsvariable auf Ω.
heißt dann eine Ω'-Zufallsvariable auf Ω.
Das Experiment, mit einem fairen Würfel zweimal zu würfeln, lässt sich mit folgendem Wahrscheinlichkeitsraum (Ω,Σ,P) modellieren:
- Ω ist die Menge der 36 möglichen Ergebnisse
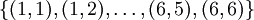
- Σ ist die Potenzmenge von Ω
- Will man zwei unabhängige Würfe mit einem fairen Würfel modellieren, so setzt man alle 36 Ergebnisse gleich wahrscheinlich, wählt also das Maß P als
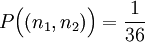 für
für 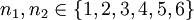 .
.
Die Zufallsvariablen X1, X2 und S werden als folgende Funktionen definiert:
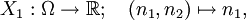
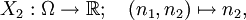 und
und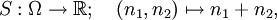
wobei für Σ' die borelsche σ-Algebra auf den reellen Zahlen gewählt wird.
In der Regel wird auf die konkrete Angabe der zugehörigen Räume verzichtet; es wird angenommen, dass aus dem Kontext klar ist, welcher Wahrscheinlichkeitsraum auf Ω und welcher Messraum auf Ω' gemeint ist.
Bei einer endlichen Ergebnismenge Ω wird Σ meistens als die Potenzmenge von Ω gewählt. Die Forderung, dass die verwendete Funktion messbar ist, ist dann immer erfüllt. Messbarkeit wird erst wirklich bedeutsam, wenn die Ergebnismenge Ω überabzählbar viele Elemente enthält.
Einige Klassen von Zufallsvariablen mit bestimmten Wahrscheinlichkeits- und Messräumen werden besonders häufig verwendet. Diese werden teilweise mit Hilfe alternativer Definitionen eingeführt, die keine Kenntnisse der Maßtheorie voraussetzen:
Reelle Zufallsvariable
Bei reellen Zufallsvariablen ist der Bildraum die Menge
 der reellen Zahlen versehen mit der borelschen σ-Algebra. Die allgemeine Definition von Zufallsvariablen lässt sich in diesem Fall zur folgenden Definition vereinfachen:
der reellen Zahlen versehen mit der borelschen σ-Algebra. Die allgemeine Definition von Zufallsvariablen lässt sich in diesem Fall zur folgenden Definition vereinfachen:- Eine reelle Zufallsvariable ist eine Funktion
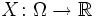 , die jedem Ergebnis ω einer Ergebnismenge Ω eine reelle Zahl X(ω) zuordnet und die folgende Messbarkeitsbedingung erfüllt:
, die jedem Ergebnis ω einer Ergebnismenge Ω eine reelle Zahl X(ω) zuordnet und die folgende Messbarkeitsbedingung erfüllt:
Das bedeutet, dass die Menge aller Ergebnisse, deren Realisation unterhalb eines bestimmen Wertes liegt, ein Ereignis bilden muss.
Im Beispiel des zweimaligen Würfelns sind X1, X2 und S jeweils reelle Zufallsvariable.
Mehrdimensionale Zufallsvariable
Die mehrdimensionale Zufallsvariable mit der Abbildung
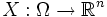 für eine Dimension
für eine Dimension 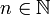 wird als Zufallsvektor aufgefasst. Damit ist
wird als Zufallsvektor aufgefasst. Damit ist 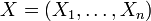 gleichzeitig ein Vektor von einzelnen reellen Zufallsvariablen
gleichzeitig ein Vektor von einzelnen reellen Zufallsvariablen 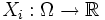 , die alle denselben Ergebnisraum Ω besitzen. Ihre Verteilung wird als multivariat bezeichnet. Sie besitzt einen Erwartungswertvektor und eine Kovarianzmatrix.
, die alle denselben Ergebnisraum Ω besitzen. Ihre Verteilung wird als multivariat bezeichnet. Sie besitzt einen Erwartungswertvektor und eine Kovarianzmatrix.Im Beispiel des zweimaligen Würfelns ist X = (X1,X2) eine zweidimensionale Zufallsvariable.
Komplexe Zufallsvariable
Bei komplexen Zufallsvariablen ist der Bildraum die Menge
 der komplexen Zahlen versehen mit der durch die kanonische Vektorraumisomorphie zwischen
der komplexen Zahlen versehen mit der durch die kanonische Vektorraumisomorphie zwischen  und
und 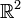 „geerbten“ borelschen σ-Algebra. X ist genau dann eine Zufallsvariable, wenn Realteil
„geerbten“ borelschen σ-Algebra. X ist genau dann eine Zufallsvariable, wenn Realteil 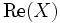 und Imaginärteil
und Imaginärteil 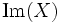 jeweils reelle Zufallsvariable sind.
jeweils reelle Zufallsvariable sind.Die Verteilung von Zufallsvariablen
Eng verknüpft mit dem eher technischen Begriff einer Zufallsvariablen ist der Begriff der auf dem Bildraum von
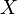 induzierten Wahrscheinlichkeitsverteilung. Mitunter werden beide Begriffe auch synonym verwendet. Formal wird die Verteilung
induzierten Wahrscheinlichkeitsverteilung. Mitunter werden beide Begriffe auch synonym verwendet. Formal wird die Verteilung 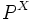 einer Zufallsvariablen
einer Zufallsvariablen 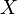 als das Bildmaß des Wahrscheinlichkeitsmaßes
als das Bildmaß des Wahrscheinlichkeitsmaßes 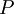 definiert, also
definiert, also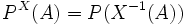 für alle
für alle 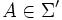 .
.
Statt
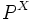 werden in der Literatur für die Verteilung von
werden in der Literatur für die Verteilung von 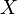 auch die Schreibweisen
auch die Schreibweisen 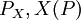 oder
oder 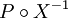 verwendet.
verwendet.Spricht man also beispielsweise von einer normalverteilten Zufallsvariablen, so ist damit eine Zufallsvariable mit Werten in den reellen Zahlen gemeint, deren Verteilung einer Normalverteilung entspricht.
Häufig wird von einer Zufallsvariablen lediglich die Verteilungsfunktion angegeben und der zu Grunde liegende Wahrscheinlichkeitsraum weggelassen. Für die mathematische Untersuchung ist der modellierte Vorgang der realen Welt uninteressant; es wird lediglich die von dieser Zufallsvariablen induzierten Verteilung mathematisch untersucht. Dies ist vom Standpunkt der Mathematik erlaubt, sofern es tatsächlich einen Wahrscheinlichkeitsraum gibt, der eine Zufallsvariable mit der gegebenen Verteilung erzeugen kann. Ein solcher Wahrscheinlichkeitsraum (Ω,Σ,P) lässt sich aber leicht angeben, indem beispielsweise
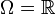 , Σ als die Borelsche σ-Algebra auf den reellen Zahlen und P als das durch die Verteilungsfunktion induzierte Lebesgue-Stieltjes-Maß gewählt wird.[3]
, Σ als die Borelsche σ-Algebra auf den reellen Zahlen und P als das durch die Verteilungsfunktion induzierte Lebesgue-Stieltjes-Maß gewählt wird.[3]Mathematische Attribute für Zufallsvariable
Verschiedene mathematische Attribute, die in der Regel denen für allgemeine Funktionen entlehnt sind, finden bei Zufallsvariablen Anwendung. Die häufigsten werden in der folgenden Zusammenstellung kurz erklärt:
diskret
Eine Zufallsvariable wird als diskret bezeichnet, wenn sie nur endlich viele oder abzählbar unendlich viele Werte annimmt. Im obigen Beispiel des zweimaligen Würfelns sind alle drei Zufallsvariable X1, X2 und S diskret.
konstant
Eine Zufallsvariable wird als konstant bezeichnet, wenn sie nur einen Wert annimmt: X(ω) = c für alle ω. Sie ist ein Spezialfall der diskreten Zufallsvariable.
unabhängig
Zwei Zufallsvariable heißen unabhängig, wenn die von ihnen erzeugten Ereignisräume stochastisch unabhängig sind. In obigem Beispiel sind X1 und X2 unabhängig voneinander; die Zufallsvariablen X1 und S hingegen nicht.
Unabhängigkeit mehrerer Zufallsvariablen
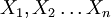 bedeutet, dass das Wahrscheinlichkeitsmaß PX des Zufallsvektors
bedeutet, dass das Wahrscheinlichkeitsmaß PX des Zufallsvektors 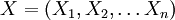 dem Produktmaß der Wahrscheinlichkeitsmaße der Komponenten, also dem Produktmaß von
dem Produktmaß der Wahrscheinlichkeitsmaße der Komponenten, also dem Produktmaß von 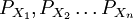 entspricht.[4] So lässt sich beispielsweise dreimaliges unabhängiges Würfeln durch den Wahrscheinlichkeitsraum (Ω,Σ,P) mit
entspricht.[4] So lässt sich beispielsweise dreimaliges unabhängiges Würfeln durch den Wahrscheinlichkeitsraum (Ω,Σ,P) mit- Ω = {1,2,3,4,5,6}3,
- Σ der Potenzmenge von Ω und
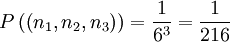
modellieren; die Zufallsvariable "Ergebnis des k-ten Wurfes" ist dann
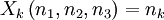 für
für 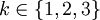 .
.
Die Konstruktion eines entsprechenden Wahrscheinlichkeitsraums für eine unendliche Folge unabhängiger Zufallsvariablen mit gegebenen Verteilungen ist ebenfalls möglich.[5]
identisch verteilt
Zwei oder mehr Zufallsvariable heißen identisch verteilt (bzw. i.d. für identically distributed), wenn ihre Verteilungen gleich sind. In Beispiel des zweimaligen Würfelns sind X1, X2 identisch verteilt; die Zufallsvariablen X1 und S hingegen nicht.
unabhängig und identisch verteilt
Häufig werden Folgen von Zufallsvariablen untersucht, die sowohl unabhängig als auch identisch verteilt sind; dieser Fall wird üblicherweise mit i.i.d. (für independent and identically distributed) bezeichnet.
In obigem Beispiel des dreimaligen Würfelns sind X1, X2 und X3 i.i.d. verteilt. S1,2 = X1 + X2 (die Summe der ersten beiden Würfe) und S2,3 = X2 + X3 (die Summe des zweiten und dritten Wurfs) sind zwar identisch verteilt, aber nicht unabhängig. S1,2 und X3 sind unabhängig, aber nicht identisch verteilt.
Mathematische Attribute für reelle Zufallsvariable
Kenngrößen
Zur Charakterisierung von Zufallsvariablen dienen einige wenige Funktionen, die wesentliche mathematische Eigenschaften der jeweiligen Zufallsvariable beschreiben. Die wichtigste dieser Funktionen ist die Verteilungsfunktion, die Auskunft darüber gibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert bis zu einer vorgegebenen Schranke annimmt, beispielsweise die Wahrscheinlichkeit, höchstens eine Vier zu würfeln. Bei stetigen Zufallsvariablen wird diese durch die Wahrscheinlichkeitsdichte ergänzt, mit der die Wahrscheinlichkeit berechnet werden kann, dass die Werte einer Zufallsvariablen innerhalb eines bestimmten Intervalls liegen. Des Weiteren sind Kennzahlen wie der Erwartungswert, die Varianz oder höhere mathematische Momente von Interesse.
stetig oder kontinuierlich
Das Attribut stetig wird für unterschiedliche Eigenschaften verwendet.
-
- Eine reelle Zufallsvariable wird als stetig (oder auch absolut stetig) bezeichnet, wenn sie eine Dichte besitzt (ihre Verteilung absolutstetig bezüglich des Lebesgue-Maßes ist).[6]
- Eine reelle Zufallsvariable wird als stetig bezeichnet, wenn sie eine stetige Verteilungsfunktion besitzt.[7] Insbesondere bedeutet das, dass P({X = x}) = 0 für alle
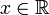 gilt.
gilt.
Messbarkeit, Verteilungsfunktion und Erwartungswert
Wenn eine reelle Zufallsvariable X auf dem Ergebnisraum Ω und eine messbare Funktion
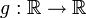 gegeben ist, dann ist auch Y = g(X) eine Zufallsvariable auf demselben Ergebnisraum, da die Verknüpfung messbarer Funktionen wieder messbar ist. Die gleiche Methode, mit der man von einem Wahrscheinlichkeitsraum (Ω,P) nach
gegeben ist, dann ist auch Y = g(X) eine Zufallsvariable auf demselben Ergebnisraum, da die Verknüpfung messbarer Funktionen wieder messbar ist. Die gleiche Methode, mit der man von einem Wahrscheinlichkeitsraum (Ω,P) nach 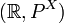 gelangt, kann benutzt werden, um die Verteilung von Y zu erhalten.
gelangt, kann benutzt werden, um die Verteilung von Y zu erhalten.Die Verteilungsfunktion von Y lautet
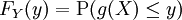 .
.
Für den Erwartungswert der Zufallsgröße Y erhält man im diskreten Fall
und im absolut stetigen Fall
![\operatorname{E}(Y) = \operatorname{E}[g(X)] = \int\limits_{-\infty}^{\infty}g(x)f_{X}(x)\operatorname{d}x](/pictures/dewiki/50/2cc34adff327f22bc2278f82fc5660bb.png) ,
,
wobei fX(x) die Dichte von X bezeichnet.
integrierbar
Eine Zufallsvariable heißt integrierbar, wenn der Erwartungswert der Zufallvariable existiert und endlich ist. Die Zufallsvariable heißt quasi-integrierbar, wenn der Erwartungswert existiert, aber unendlich ist.
Beispiel
Es sei X eine reelle stetig verteilte Zufallsvariable und Y = X2.
Dann ist
Fallunterscheidung nach y:
y < 0:
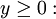
standardisiert
Eine Zufallsvariable nennt man standardisiert, wenn ihr Erwartungswert 0 und ihre Varianz 1 ist. Die Transformation einer Zufallsvariable Y in eine standardisierte Zufallsvariable
bezeichnet man als Standardisierung der Zufallsvariable Y.
Sonstiges
- Zeitlich zusammenhängende Zufallsvariable können auch als stochastischer Prozess aufgefasst werden
- Eine Folge von Realisationen einer Zufallsvariable nennt man auch Zufallssequenz
Belege
- ↑ Die nötigen Voraussetzungen werden im Absatz Definition angegeben.
- ↑ Karl Hinderer: Grundbegriffe der Wahrscheinlichkeitstheorie. Springer, Berlin 1980. ISBN 3-540-07309-4 (nicht überprüft)
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3 (Definition 5.6.2)
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3 (Definition 5.8.1)
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3 (Theorem 5.11.1)
- ↑ Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. VEB Deutscher Verlag der Wissenschaften, Berlin 1989 (11.Aufl., Definition 2.3.3)
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972, S.210. ISBN 0-12-065201-3
Literatur
- Karl Hinderer: Grundbegriffe der Wahrscheinlichkeitstheorie. Springer, Berlin/Heidelberg/New York 1980, ISBN 3540073094
- Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck & Ruprecht, Göttingen 1974, ISBN 3525031149
Weblinks
- Statistik III – Skript zur Vorlesung von Leonhard Held, Ludwig-Maximilians-Universität München, 2006
Wikimedia Foundation.

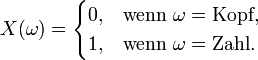
![\operatorname{E}(Y) = \operatorname{E}[g(X)] = \sum_{i=1}^{\infty}g(x_{i}) P(X=x_{i})](/pictures/dewiki/48/0b45bd922e5630932a8c19b11d627330.png)