Cos4-Gesetz

Helligkeitsabfall für verschiedene Brennweiten, bezogen auf das Kleinbildformat (43,2 mm Diagonale)

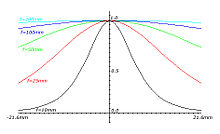
Das Cos⁴-Gesetz (lies: Kosinus-hoch-4-Gesetz) beschreibt den natürlichen Randlichtabfall. Es besagt, dass die Bildhelligkeit beim Abbilden eines gleichmäßig hellen Motivs durch ein Objektiv um den Faktor cos⁴α gegenüber der Helligkeit in der Bildmitte abnimmt. Die Bildhelligkeit B(α) im Winkel α außerhalb der Bildmitte beträgt

$B(\alpha) = B_0 \cdot \cos^4 \alpha$.

Das Gesetz gilt unter den Voraussetzungen, dass die Abbildung verzeichnungsfrei ist und das Objektiv nicht vignettiert und keine Pupillenaberration aufweist und sonstige Lichtverluste, etwa durch Reflexion an den Linsenoberflächen, vernachlässigt werden. In der Praxis sind diese Voraussetzungen aber oft nicht erfüllt. Die meisten Objektive vignettieren bei weit geöffneter Blende, was den Helligkeitsabfall verstärkt, und die Pupillenaberration vieler Weitwinkelobjektive vermindert den Helligkeitsabfall erheblich.

Ursachen

Veranschaulichung des für die Bildhelligkeit relevanten Raumwinkels ω

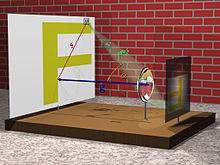
Im Cos4-Gesetz sind verschiedene Faktoren zusammengefasst. Zur Veranschaulichung der einzelnen Ursachen für den natürlichen Randlichtabfall geht man von einem flächenhaften Motiv aus, z. B. einer gleichmäßig ausgeleuchteten Wand mit der Leuchtdichte L. Diese Voraussetzung gilt nicht für alle Objektive. Siehe Abschnitt Objektivkonstruktionen.

Die Abbildung soll mit einer idealen Linse erfolgen. Betrachtet man ein infinitesimales Oberflächenelement der Wand von der Größe $dA = dx\cdot dy$, das sich auf der optischen Achse befinden soll, dann beträgt die photometrische Lichtstärke I senkrecht zur Oberfläche (also in Richtung der Linse)

$I = dA \cdot L$.

Der die Linse durchsetzende Lichtstrom Φ ist vom Raumwinkel ω des Lichtkegels abhängig, der durch die Linse (Kegelbasis) und den Objektpunkt (Kegelspitze) gebildet wird:

$\qquad\qquad\Phi = \omega \cdot I$(Gleichung 1)

Liegt das Oberflächenelement auf der optischen Achse, so ergibt sich der Raumwinkel ω aus Linsendurchmesser d und dem Abstand g zur Wand (näherungsweise für $d \ll g$):

$\omega = \frac{d^2}{4\cdot g^2}\cdot 1sr$

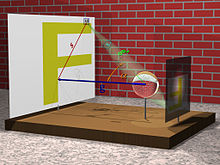
Verschiebt man nun das Oberflächenelement seitlich um einen Betrag s, so dass es von der Linse aus gesehen unter dem Winkel α zur optischen Achse erscheint, dann ändern sich sowohl die photometrische Lichtstärke I also auch der Raumwinkel ω:

Veranschaulichung des Cos4-Gesetzes

Reduktion der photometrischen Lichtstärke

Das Oberflächenelement erscheint nun von der Linse aus betrachtet um den Faktor cos(α) verkürzt, weil es um den Winkel α zur Blickrichtung gekippt ist (perspektivische Verkürzung) und deshalb entsprechend weniger Licht in Richtung der Linse aussendet (lambertsches Gesetz).

Daraus ergibt sich der erste Cosinus-Faktor:

$\qquad\qquad I' = I\cdot \cos \left(\alpha \right)$(Gleichung 2)

Reduktion des Raumwinkels ω

Das Verschieben des Motivs hat die Entfernung g wie folgt vergrößert:

$g' = \frac{g}{\cos \left(\alpha \right)}$

Die Linse erscheint nun außerdem vom Objektpunkt aus gesehen nicht mehr kreisförmig, sondern als Ellipse, deren kurze Achse zu $q = d \cdot \cos(\alpha)$ verkürzt wurde.

Hier muss die Freiheit von Vignettierung und Pupillenaberration vorausgesetzt werden. Bei der Einzellinse ist der Linsenrand zugleich die Blende und damit die Eintrittspupille (EP) des Systems. In einem komplexeren System wird die Blende von den vor der Blende liegenden Linsen auf die EP abgebildet, wobei sie mehr oder weniger verzerrt wird (Pupillenaberration). Die EP begrenzt dann das einfallende Strahlenbündel, und sie kann mehr oder weniger Licht einlassen als bei unverzerrter Abbildung. Außerdem kann das einfallende Strahlenbündel noch von festen Blenden oder Linsenrändern beschnitten werden (Vignettierung), so dass es nicht mehr die ganze EP ausfüllt.

Damit verkleinert sich der Raumwinkel schließlich zu:

$\omega' = \frac{d\cdot q}{4\cdot g'^2}\cdot 1sr = \frac{\cos^3\alpha\cdot d^2}{4\cdot g^2} \cdot 1sr$,

und das ist:

$\qquad\qquad \omega' = \omega\cdot \cos^3\alpha$(Gleichung 3)

Analog zu Gleichung 1 ergibt sich der resultierende Lichtstrom Φ zu

$\Phi' = \omega'\cdot I'$.

Setzt man ω' und I aus den Gleichungen 2 und 3 ein, ergibt sich:

$\Phi' = \Phi\cdot \cos^4\alpha$

Der Bildwinkel β entspricht dabei dem doppelten von α, denn er überstreicht denselben Winkel auch auf der α gegenüberliegenden Seite der optischen Achse, also gilt:

$\Phi' = \Phi \cdot \cos^4 \left(\frac \beta 2 \right)$

Dieser Ausdruck gibt an, wieviel Lichtstrom von einem kleinen, im Winkel α = β / 2 zur Achse stehenden Flächenelement durch eine kreisförmige Öffnung (hier der Linsenrand) tritt. Er gilt universell, selbst wenn überhaupt keine abbildende Optik vorhanden ist.

Wird nun das Flächenelement dA von der Linse bzw. dem Objektiv verzeichnungsfrei und ohne weitere Lichtverluste mit dem Abbildungsmaßstab m auf die Bildebene abgebildet, so nimmt es unabhängig von α immer die gleiche Fläche $dA' = m^2 \cdot dA$ auf dem Bild ein. Die Beleuchtungsstärke E der Bildebene an dieser Stelle beträgt dann

$E = \frac {\Phi'} {dA'} = \frac {\Phi'} {m^2 \cdot dA} = \frac {\Phi} {m^2 \cdot dA} \cos^4 \left(\frac \beta 2 \right)$

Somit nimmt die Beleuchtungsstärke des Bildes unter den beschriebenen Voraussetzungen mit dem Faktor $\cos^4 \left(\frac \beta 2 \right)$ ab (Cos4-Gesetz).

Wenn das Objektiv andererseits verzeichnet, dann hängt die Fläche des Bildelements dA' vom Bildwinkel ab. Einen erheblichen Einfluss hat dies bei Fischaugenobjektiven, die stark tonnenförmig verzeichnen. Mit zunehmendem Bildwinkel α wird hier dA' immer kleiner, und das Licht konzentriert sich auf eine kleinere Fläche, was eine höhere Beleuchtungsstärke und somit eine Verminderung des Randlichtabfalls ergibt.

Bei Lichtverlusten innerhalb des optischen Systems – z. B. durch Filter, Blenden, Reflexions- und Absorptionsverluste – die das Bildfeld gleichmäßig abdunkeln, entspricht die gemessene Helligkeitsverteilung immer noch dem Cos4-Gesetz, denn dieses macht ja keine konkreten Helligkeitsangaben, sondern beschreibt das Verhältnis der Helligkeiten im Zentrum bzw. am Rand des Bildfeldes. Das gilt jedoch nicht für bildwinkelabhängige Lichtverluste.

Gegenmaßnahmen

Abbildung mit einer Kugellinse

Die scheinbare Verkleinerung des Oberflächenelementes dA durch die perspektivische Verkürzung und die Vergrößerung seines Abstandes vom Objektiv lässt sich nicht beeinflussen. Doch das „Zusammenquetschen“ des Lichtkegels durch die perspektivische Verkürzung der Linse (beziehungsweise der Eintrittspupille als Bild der Blende bei einem Objektiv) zur Ellipse lässt sich mit technischen Maßnahmen reduzieren.

So könnte man eine Linse durch eine Glaskugel (oder eine Schusterkugel) ersetzen – deren Projektion erscheint unter jedem Winkel als Kugel und erfährt daher keine perspektivische Verkürzung.

In realen Objektiven nutzt man zu diesem Zweck oft eine Pupillenaberration: Die Linsen vor der Blende, die diese auf die Eintritspupille (EP) abbilden, werden so ausgelegt, dass die EP verzerrt wird. Mit zunehmendem Einfallswinkel β / 2 des Lichts wird die Fläche der EP größer. Der Querschnitt des vom Objektiv eingelassenen Strahlenbündels reduziert sich dadurch um weniger als den Faktor cos(β / 2), und bei entsprechend starker Pupillenaberration kann er sogar größer werden. Mit vertretbarem Aufwand kann der Helligkeitsabfall um maximal etwa zwei Kosinus-Faktoren vermindert werden:

$B(\beta) \, \approx \, B(0) \cdot \cos\left(\frac \beta 2 \right)^2$

Allerdings ist eine so starke Pupillenaberration mit beträchtlichem Aufwand verbunden. Die dadurch entstehen Abbildungsfehler müssen durch die Linsen nach der Blende wieder korrigiert werden. Der Helligkeitsgewinn fällt außerdem erst bei großen Bildwinkeln β deutlich ins Gewicht, deshalb kommt eine auf diesem Prinzip basierende Korrektur in der Fotografie erst bei Weitwinkel-Objektiven mit großen Bildwinkeln zur Anwendung.

Stitching

Dem Randlichtabfall kann bei der Aufnahme von unbewegten Motiven durch Stitching entgegengewirkt werden. Dabei werden einzelne Aufnahmen zu einer Aufnahme mit einem größeren Bildwinkel kombiniert. Die Kamera wird zwischen den einzelnen Aufnahmen jeweils horizontal bzw. vertikal um einen kleinen Winkel geschwenkt. Dadurch wird auch die Schärfeebene (ähnlich wie bei einem Fischaugenobjektiv – siehe nächster Abschnitt) und die Bildebene jeweils geschwenkt. Der Randlichtabfall kann dadurch im Prinzip völlig eliminiert werden. Während dem Randlichtabfall durch Stitching entgegengewirkt werden kann, wirkt sich umgekehrt der durch den Randlichtabfall verursachte Helligkeitsunterschied gerade beim Kombinieren von Aufnahmen besonders störend aus, vor allem wenn die Einzelaufnahmen selbst bereits einen größeren Bildwinkel abdecken.

Objektivkonstruktionen

Einige Objektivkonstruktionen zeigen einen gegenüber dem Cos4-Gesetz unterschiedlichen Randlichtabfall:

Objektseitig telezentrisches Objektiv

Objektseitig telezentrische Systeme weisen einen (prinzipiell korrigierbaren) natürlichen Randlichtabfall von

$B' = B\cdot {\frac {f}{\sqrt{{\left(\frac {d}{2} \right)}^2 + f^2}}}$

am Rand des Bildkreises auf. Da bei ihnen der Bildwinkel immer 0° beträgt, tritt immer dieselbe Lichtmenge durch die Frontlinse. Objektseitig telezentrische Systeme besitzen jedoch eine Blende im bildseitigen Brennpunkt, die von den Randstrahlen – abhängig vom Frontlinsendurchmesser und der Brennweite – schräg durchsetzt wird. Daher wird das Strahlenbündel auf einen elliptischen Querschnitt reduziert, und das bewirkt den genannten Randlichtabfall.

Fischaugenobjektiv

Bei Fischaugenobjektiven ist die Schärfeebene nicht flach, sondern hat die Form einer Kugelschale. Dadurch wird es erst möglich, Bildwinkel von 180° und sogar darüber hinaus abzubilden. Das heißt aber auch, dass man das Flächenstück nicht mehr einfach, wie im Abschnitt Ursachen dargestellt, senkrecht zur optischen Achse verschieben darf; man muss es stattdessen auf der Kugelschale verschieben bzw. um das Zentrum der Kugel rotieren.

Befindet sich das Zentrum der Kugel nahe dem Objektiv, so verändert sich die Entfernung des Flächenelementes bei der Verschiebung nicht. Es gibt auch keine perspektivische Verzerrung des Flächenelementes mehr, denn dieses hat seine Orientierung im Raum ebenfalls verändert, so dass seine Flächennormale immer noch zur Linse weist. Einzig die (prinzipiell korrigierbare) perspektivische Verzerrung der Blende zu einer Ellipse führt zu einem Randlichtabfall von

$B' = B\cdot \cos\left(\frac \beta 2 \right)$

relativer Helligkeitsabfall

Während der absolute Helligkeitsabfall also nur unwesentlich beeinflusst werden kann, kann der relative Helligkeitsabfall hingegen einfach korrigiert werden, indem das Bild einfach im Bildzentrum abgedunkelt wird. So werden bei extremen Weitwinkelobjektiven beispielsweise Centerfilter eingesetzt, die bevorzugt die Bildmitte abdunkeln.

Durch das Abdunkeln mit einem Centerfilter wird zwar das Bild insgesamt dunkler (der absolute Helligkeitsabfall wird also noch größer), so dass bei der Fotografie längere Belichtungszeiten erforderlich werden. Aber der Helligkeitverlauf ist dafür weniger steil, somit wird ein größerer Bildkreis gleichmäßig ausgeleuchtet.

Siehe auch

• Linsengleichung

Weblinks

• Aperture and Pupil. Skript zur Vorlesung Optical System Design Department of Physics at National Cheng Kung University, 2001 (PDF, englisch; 1,05 MB)
• Douglas A. Kerr: Derivation of the “Cosine Fourth” Law for Falloff of Illuminance Across a Camera Image. 2007 (PDF, englisch)