Coupled Cluster

Theoretische Chemie ist die Anwendung nichtexperimenteller (üblicherweise mathematischer oder computersimulationstechnischer) Methoden zur Erklärung oder Vorhersage chemischer Phänomene. Daher beschäftigt sie sich in erster Linie mit der Entwicklung beziehungsweise Weiterentwicklung von Methoden, mit denen die chemischen und physikalischen Eigenschaften der Materie berechnet werden können, sowie mit deren computertechnischen Implementierung durch Programme meist in Fortran oder C. Die entwickelten Computerprogramme werden dann im Rahmen der Computerchemie nicht nur von Vertretern der Theoretischen Chemie, sondern auch von anderen Bereichen der Chemie zur Unterstützung bei der Lösung von chemischen Problemstellungen verwendet. Untergeordnet werden auch neue Ansätze zur Interpretation von Ergebnissen erforscht.

Ab-initio-Methoden

Methoden, die von der Schrödingergleichung bzw. deren relativistischen Erweiterung (Dirac-Gleichung) ausgehen, enthalten als Parameter nur Naturkonstanten, und werden daher als Ab-initio-Methoden bezeichnet. Diese Methoden sind wissenschaftlich am besten fundiert, können allerdings nur auf relativ kleine Systeme mit relativ wenigen Atomen angewendet werden, wenn quantitativ genaue Ergebnisse erwünscht werden. Dies liegt darin begründet, dass die Schrödinger- bzw. Dirac-Gleichung nur für einige triviale Einelektronensysteme analytisch gelöst werden können und ansonsten Näherungslösungen notwendig sind, welche mit zunehmenden Systemumfang jedoch schnell eine zu hohe Rechenleistung in Anspruch nehmen. Computerprogramme zur Ab-initio-Berechnung von chemischen Strukturen sind beispielsweise GAUSSIAN und GAMESS.

Die Schrödingergleichung ist eine Eigenwertgleichung (partielle Differentialgleichung)und hat folgende Form:

Operator * (Eigen)funktion = Eigenwert * (Eigen)funktion.

Im zeitunabhängigen Fall besteht diese aus dem sogenannten Hamiltonoperator Ĥ, der Wellenfunktion Ψ und der Gesamtenergie E des Systems, wobei

$\hat{H} \Psi = E \Psi$

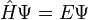
gilt. Der (bekannte) Hamiltonoperator beschreibt dabei die kinetischen und potentiellen Energien der beteiligten Teilchen (Elektronen und Atomkerne). Er wirkt auf die (unbekannte) Wellenfunktion Ψ. Das Betragsquadrat von Ψ, also ΨΨ ^* wird als Wahrscheinlichkeitsdichte der beteiligten Teilchen des Systems interpretiert. Wenn Ψ bekannt ist, können alle Eigenschaften eines Systems relativ einfach als Erwartungswert über den jeweiligen Operator berechnet werden.

Born-Oppenheimer-Näherung

Aufgrund des großen Masseunterschieds zwischen Elektronen und Atomkernen kann die Bewegung der Atomkerne in meist sehr guter Näherung abgetrennt werden, wobei nach weiterer Abtrennung der Translation des Gesamtsystems eine Kernschrödingergleichung resultiert, welche die Schwingung und Rotation des Systems, zum Beispiel eines Moleküls, beschreibt. Übrig bleibt die elektronische Schrödingergleichung, die für feste Atomkernlagen punktweise gelöst werden kann. Die sich dabei ergebenden (elektronischen) Energien fließen in die Kernschrödingergleichung mit ein.

Qualitativ bedeutet dies, dass die Elektronen sich im Potential der Atomkerne bewegen, und sich auf Änderungen der Kerngeometrie augenblicklich einstellen. Ihre Grenze findet diese Näherung dort, wo eine geringe Änderung der Kerngeometrie mit einer großen Änderung der Elektronenstruktur verbunden ist. Solche Situationen findet man gelegentlich an bestimmten Geometrien von vieratomigen oder noch größeren Molekülen, insbesondere, wenn diese sich in einem elektronisch angeregten Zustand befinden.

Die Born-Oppenheimer-Näherung ermöglicht erst die Vorstellung, dass Moleküle eine Gleichgewichtsgeometrie besitzen, um die ihre Atome dann schwingen. Mathematisch bedeutet die Born-Oppenheimer-Näherung, dass in der elektronischen Schrödingergleichung der Term für die kinetische Energie der Kerne gleich Null gesetzt wird und der Term für die potentielle Energie der Kern-Kern-Wechselwirkung zu einem Parameter wird, der durch das Coulomb-Gesetz und die gewählte Anordnung der Atomkerne bestimmt ist.

Die Lösung der Gesamtschrödingergleichung, die auch die kinetische Energie der Kerne umfasst, ist nur für das kleinste System, das Wasserstoffmolekül praktisch möglich. Stattdessen wird in zwei Schritten zunächst die elektronische Schrödingergleichung an ausgewählten Kerngeometrien gelöst, dann basierend auf diesen Daten eine analytische Näherungslösung der Energiehyperfläche gesucht und diese dann in die Kernschrödingergleichung eingesetzt. Dabei muss gesagt werden, dass die Kernschrödingergleichung vergleichsweise selten gelöst wird, da man sich aus zeitlichen Gründen auf wenige Freiheitsgrade des Systems beschränken muss (ein System aus N-Atomen besitzt 3N-6 Freiheitsgrade) und es außerdem Möglichkeiten gibt, Größen wie die Schwingungsfrequenzen von Molekülen auf andere Weise in guter Näherung zu berechnen (siehe unten bei Berechnung physikalischer Eigenschaften)

Hartree-Fock-Methode

Unter Hartree-Fock-Rechnung versteht man eine Ab-initio-Methode der Theoretischen Chemie, um Eigenschaften von Mehrelektronensystemen, die analytisch nicht mehr lösbar sind, näherungsweise zu berechnen. Namensgeber hierfür sind Douglas Rayner Hartree und Wladimir Alexandrowitsch Fock. Bei dieser Methode wird die Wellenfunktion näherungsweise als Determinante aus Einelektronenfunktionen (den sogenannten Orbitalen) angesetzt, wobei diese wiederum in der Regel als Linearkombination von sogenannten (in der Regel Atom-zentrierten) Basisfunktionen mit unbekannten Koeffizienten angesetzt werden. Die Lösung der Hartree-Fock-Gleichung wird damit letztlich auf die Berechnung von Integralen über die Basisfunktionen und die Diagonalisierung einer Matrix zurückgeführt. Diese Rechenoperationen lassen sich mit Computern im Gegensatz zur Lösung von Differentialgleichungen mehrerer Variablen sehr effizient lösen. Bei sogenannten Open-Shell Systemen können zur Respektierung der Symmetrie statt einer Determinante auch Linearkombinationen von Determinanten mit durch Symmetrie vorgegebenen Koeffizienten vorkommen.

Multi-Configuration-SCF Wellenfunktionen

In manchen Fällen genügt es nicht, die Wellenfunktion als eine Determinante (bzw. mit mehreren aber mit festen Koeffizienten) anzusetzen, um das System qualitativ richtig zu erfassen. Stattdessen müssen die relevanten Determinanten identifiziert werden und deren Koeffizienten zusammen mit den Orbitalen optimiert werden. Eine solche Vorgehensweise ist oft bei der Beschreibung von elektronisch angeregten Zuständen erforderlich. Die gezielte Auswahl dieser Determinanten gestaltet sich allerdings als schwierig und hängt zudem in gewissem Maße von der betrachteten Geometrie des Moleküls ab. Daher werden oft nicht einzelne Determinanten, sondern besonders relevante Orbitale (zum Beispiel die (energetisch) höchsten besetzten und tiefsten unbesetzten: HOMO, LUMO) betrachtet und alle Determinanten, die sich durch Ersetzen von den betrachteten besetzten durch unbesetzte erzeugt werden können, berücksichtigt. Dieser Ansatz wird als Complete Active Space Self Consistent Field (CASSCF) bezeichnet. Aufgrund der exponentiell anwachsenden Anzahl ist die maximale Zahl der derart zu berücksichtigten Orbitale auf ca. 12-16 beschränkt.

Korrelierte Rechnungen

Die Genauigkeit der Hartree-Fock bzw. MCSCF / CASSCF Lösungen ist in der Regel nicht genügend hoch, so dass daran anschließend für gewöhnlich eine korrelierte Rechnung durchgeführt wird, wobei die bei der Lösung der Hartree-Fock-Gleichung anfallenden unbesetzten Orbitale zum Einsatz kommen. Die Zahl der berechneten Orbitale entspricht nämlich der Zahl der eingesetzten Basisfunktionen und ist in der Regel signifikant größer als die Zahl der besetzten Orbitale, die Teil der Hartree-Fock bzw. MCSCF-Wellenfunktion sind. Im Prinzip wird bei korrelierten Methoden die Wellenfunktion als Linearkombination von Determinanten angesetzt mit der Hartree-Fock Wellenfunktion als führende Determinante (großer Koeffizient). Weitere Determinanten werden gebildet, indem besetzte Orbitale durch unbesetzte Orbitale ersetzt werden (sogenannte Anregungen).

Bei den korrelierten Methoden werden im Single-Referenz Fall für gewöhnlich entweder die Störungstheorie (Moller-Plesset Ansatz) oder Coupled Cluster (CC) Ansätze eingesetzt, bei Multi-Referenzmethoden entweder die Multi-Referenz Configuration Interaction MRCI Methode oder die Multi-Referenz Störungstheorie.

In der Regel werden bei allen Methoden Ein- und Zweifachanregungen bzgl. der Referenz-Wellenfunktion berücksichtigt, wobei aufgrund der Art des Coupled Cluster Ansatzes hier auch bestimmte Klassen höherer Anregungen mit berücksichtigt werden.

Bei der Configuration Interaction Methode werden zunächst bezüglich der Referenz-Wellenfunktion (SCF bzw. MCSCF/CASSCF) z.B. alle Ein- und Zweifachanregungen erzeugt, indem ein bzw. zwei besetzte Orbitale durch die entsprechende Anzahl unbesetzter Orbitale ersetzt werden. Die CI-Wellenfunktion wird als Linearkombination aller dieser Determinanten angesetzt und die entsprechenden (CI-) Koeffizienten der Determinanten so bestimmt, dass die resultierende Energie minimal (möglichst negativ) ist. Üblicherweise werden nur Ein- und Zweifachanregungen berücksichtigt. Ein Sonderfall ist das sogenannte Full-CI, bei welchem alle möglichen Anregungen erzeugt werden. Full-CI Rechnungen sind aber mit einem so großen Rechenaufwand verbunden, so dass sie nur bei kleinen Systemen als Benchmark durchgeführt werden können. Die MRCI(SD) Methode gilt als sehr genau.

Bei Störungsrechnungen wird der Hamiltonoperator H als Summe eines ungestörten Operators Ĥ⁽⁰⁾ und eines Störoperators Ĥ⁽¹⁾ aufgespalten, wobei die Störung „klein“ sein soll. Die Eigenwertlösungen des ungestörten Operators Ĥ⁽⁰⁾ sind dabei bekannt. Bei korrelierten Störungsrechnungen wird als Ĥ⁽⁰⁾ derjenige Operator verwendet, der als Lösungen die Hartree-Fock bzw. die MCSCF/CASSCF Wellenfunktionen zur Lösung hat. Ĥ⁽¹⁾ ergibt sich dann als Differenz zum echten Hamiltonoperator des Systems. Häufig werden im Single-Referenz Fall die MP2 oder die MP4(SDQ) Methodik eingesetzt, im Multireferenzfall die sogenannte CASPT2 Methode (mit einer CASSCF Wellenfunktion als Referenz-Wellenfunktion), seltener die CASPT3 Methode.

Bei der Lösung der Störungsgleichung ergibt sich, dass der gestörte Anteil sich weiter aufspaltet in eine Wellenfunktion erster Ordnung, zweiter Ordnung usw., wobei sich die Gesamtwellenfuktion als Summe der ungestörten sowie der verschiedenen gestörten Wellenfunktionen ergibt. Der rechnerische Aufwand wird mit jeder hinzukommenden Korrektur deutlich höher. Es ist allerdings nicht zwangsläufig, dass die Reihe gegen das exakte Ergebnis konvergiert, d.h. dass es nicht gewährleistet ist, dass die berechnete Wellenfunktion und die zugehörige Energie / Eigenschaften mit steigendem Aufwand immer besser werden. In der Tat werden teilweise auch Oszillationen bzw. Divergenz der Ergebnisse beobachtet.

Beim Coupled-Cluster Ansatz wird die Wellenfunktion als Ψ = exp(H) Ψ(0) dargestellt. Dies garantiert einerseits die Größenkonsistenz der Methode und führt andererseits dazu, dass bestimmte höhere Anregungstypen ebenfalls erfasst werden. Coupled Cluster Rechnungen vom CCSD(T) Typ gelten als sehr genau. Die Wellenfunktion liegt hier nicht in geschlossener Form vor, so dass die Eigenschaften auf andere Weise berechnet werden müssen, wofür aber entsprechende Vorgehensweisen existieren.

Die Configuration Interaction Methode ist variationell, das heißt die berechnete Energie liegt immer über der exakten Energie. Dies gilt jedoch nicht für die Störungstheorie oder den Coupled Cluster Ansatz. Allerdings sind Störungstheorie und Coupled Cluster Ansatz im Gegensatz zur CI-Methode größenkonsistent. Größenkonsistenz bedeutet, dass die Energie, die sich bei der Berechnung eines Supersystems von zwei aufgrund des großen gewählten Abstands praktisch nicht-miteinander wechselwirkenden (gleichen) Molekülen ergibt, gleich sein muss mit der doppelten berechneten Energie eines einzelnen Moleküls. Aufgrund dieses Mankos der CI-Methode werden heutzutage keine CI-Rechnungen auf (Single-Referenz) Hartree-Fock Rechnungen mehr aufgesetzt, wohingegen MRCI(SD) Rechnungen als sehr genau gelten. Full-CI Rechnungen, bei denen alle im Orbitalraum möglichen Anregungen bzgl. der SCF bzw. MCSCF Funktion berücksichtigt werden, sind als Sonderfall sowohl variationell als auch größenkonsistent, allerdings mit Abstand auch am teuersten.

Der Aufwand bei der Durchführung korrelierter Methoden steigt nicht linear mit der Größe des Moleküls, sondern liegt bei den üblicherweise benutzen Methoden zwischen N⁵ und N⁷, wobei N ein Maß für die Größe des Moleküls (etwa die Zahl der Basisfunktionen) ist. Dies kann darauf zurückgeführt werden, dass die Orbitale delokalisiert, d.h. mehr oder weniger über das ganze Molekül ausgebreitet sind. Die sich bei der Hartee-Fock-Rechnung ergebenden Orbitale lassen sich jedoch mit verschiedenen Methoden relativ gut lokalisieren. Korrelationsmethoden, die diese lokalisierten Orbitale verwenden, versprechen eine deutliche Reduktion des obigen Skalierungsverhaltens mit der Molekülgröße und werden intensiv erforscht.

Semiempirische Methoden

Bei den sogenannten semiempirischen Methoden werden im allgemeinen die Matrixform der Hartree-Fock-Gleichung vereinfacht, indem bestimmte Größen in der Matrixgleichung entweder vernächlässigt, durch experimentell bestimmte Werte ersetzt oder an einem Trainingssatz justiert werden. Ein solcher Trainingssatz besteht in der Regel aus (experimentellen) Größen wie Bindungsabstände, Dipolmomente etc. von einer Reihe von Molekülen, die durch Variation der freien Parameter möglichst gut reproduziert werden sollen. Semiempirische Methoden können Systeme mit (mindestens) mehreren 100 Atomen behandeln.

Dichtefunktionale

Bei der Dichtefunktionaltheorie (DFT) macht man sich die Tatsache zunutze, dass zur Beschreibung des Grundzustandes die Elektronendichte unabhängig von der Zahl der Elektronen als Funktion von nur drei Ortsvariablen notwendig ist; gegebenenfalls kommt eine weitere Funktion für die Spindichte dazu. Allerdings besteht hier das Problem, dass die notwendigen Terme (Operatoren) in der zu lösenden Gleichung nicht alle genau bekannt sind, sondern teilweise Näherungen notwendig sind. Heutige Dichtefunktionale erreichen die Genauigkeit von einfachen korrelierten Ab-initio-Methoden (wie die Störungstheorie zweiter Ordnung) und können für Systeme bis ca. 1000 Atomen eingesetzt werden. Häufig verwendet man DFT-Rechnungen zur Geometrieoptimierung von Molekülen.

Kraftfelder

Bei den sogenannten Kraftfeldmethoden greift man dagegen auf eine klassische Vorstellungsweise zurück, gemäß welcher die Atome in Molekülen durch kleine Federn mit bestimmter Federkonstante miteinander verbunden sind, welche auch die Änderung von Bindungs- und Torsionswinkeln beschreiben. Diese Methode ist besonders für sehr große (Bio-)Moleküle geeignet, die mit anderen Methoden nicht bewältigt werden können, und dient hauptsächlich zu deren Geometrieoptimierung. Allerdings müssen für eine Vielzahl von möglichen Atomkombinationen (zwei für Bindungen, drei für Bindungswinkel, vier für Torsionswinkel) entsprechende Federkonstanten ermittelt werden. (Partielle) Ladungen auf Atomen und deren Wechselwirkung miteinander werden ebenfalls berücksichtigt. Die Beschreibung von Bindungsbrüchen ist bei dieser Methodik inhärent problematisch.

Kraftfeldmethoden können viele konformationelle Fragen beantworten. Kraftfelder werden zum Beispiel bei klassischer Moleküldynamik benutzt.

Berechnung physikalischer Eigenschaften

Den physikalischen Eigenschaften eines Systems wie sein Dipolmoment μ ist ein quantenchemischer Operator zugeordnet. Bei Kenntnis der Wellenfunktion Ψ kann die Eigenschaft als Erwartungswert über den Operator berechnet werden, das Dipolmoment also als 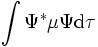$\int \Psi^* \mu \Psi \mathrm d\tau$. Außerdem kann die Eigenschaft auch als ein- oder mehrfache Ableitung der elektronischen Energie des Systems nach bestimmten Größen ermittelt werden, die von der physikalischen Eigenschaft abhängen. Die letztere Methode kann auch verwendet werden, wenn die Wellenfunktion explizit nicht bekannt ist (etwa beim coupled cluster Ansatz) und ist im Gegensatz zur ersten Methode nicht auf die Gleichgewichtsgeometrie beschränkt.

Geometrieoptimierung

Da die Lösung der Schrödingergleichung nur punktweise, das heißt für diskrete Geometrien möglich ist und eine hinreichend genaue Lösung für eine Geometrie bereits mit einem hohen Rechenaufwand verbunden ist, beschäftigt sich ein Teilzweig der Theoretischen Chemie mit der Aufstellung von Algorithmen, mit denen ausgezeichnete Geometrien mit möglichst geringem rechnerischen Aufwand gefunden werden können. Ausgezeichnete Geometrien sind zum Beispiel die Gleichgewichtsgeometrie (energetisches Minimum), sowie bei chemischen Reaktionen der Übergangszustand als Sattelpunkt auf der Reaktionskoordinate. Die Energiedifferenz zwischen Edukten und Übergangszustand bestimmt die Aktivierungsenergie der Reaktion, die Energiedifferenz zwischen Edukten und Produkten die Reaktionsenergie. Häufig werden Methoden eingesetzt, in welchen neben der Energie an einem Punkt auch dessen erste Ableitung berechnet und die zweite Ableitung abgeschätzt wird.

Simulation chemischer Reaktionen

Zur Simulation chemischer Reaktionen ist im allgemeinen eine analytische Darstellung der beteiligten Energiehyperfläche(n) im relevanten Bereich der möglichen Geometrien des zu betrachteten Systems (z.B. Moleküls) notwendig, also eine analytische Funktion, die die Energie des Systems in Abhängigkeit von seiner Geometrie wiedergibt. Dazu wird für jede Fläche an bestimmten ausgezeichneten Geometrien die zugehörigen Energie berechnet und davon ausgehend eine approximative analytische Darstellung der Fläche ermittelt, wofür es verschiedene Ansätze gibt. Da die Zahl der internen Freiheitsgrade eines Systems, das aus N Atomen besteht, 3N-6 beträgt (lineare Moleküle 3N-5), kann eine vollständige Energiehyperfläche, also eine, welche alle Freiheitsgrade des Systems berücksichtigt, nur für drei bis maximal vieratomige Moleküle berechnet werden. Bei größeren Systemen muss eine Auswahl der relevanten Geometrieparameter (d.h. in der Regel bestimmte Bindungsabstände, Winkel oder Torsionswinkel) getroffen werden, wobei die Werte der restlichen Geometrieparamter an den ausgezeichneten Geometrien energetisch optimiert werden. Nachdem die Flächen in analytischer Form vorliegen, kann die Kernschrödingergleichung gelöst und so das Fortschreiten der chemischen Reaktion am Computer simuliert werden. Auch hierzu existieren verschiedene Ansätze.

Qualitative Erklärungsschemata

Vor allem in der Frühzeit der theoretischen Chemie wurde eine Reihe von Erklärungsschemata aufgestellt, mit deren Hilfe verschiedene Aspekte qualitativ erklärt werden konnten. Ein Beispiel ist die sogenannte VSEPR-Theorie, mit deren Hilfe sich die Geometrie einfacher Moleküle mit einem Zentralatom voraussagen lässt. Aber auch in jüngerer Zeit wurden neue Konzepte entwickelt, etwa die electron localization function (ELF) oder das topologische Konzept von Richard Bader (atoms in molecules 1990). ELF ist eine Methode, um chemische Bindungen sichtbar zu machen. Sie beruht auf der Paardichte von zwei Elektronen mit gleichem Spin (same spin pair probability density). Orte mit geringer Paardichte werden mit einer hohen Lokalität eines Elektrons und topologisch mit einer chemischen Bindung in Zusammenhang gebracht. ELF kann auf HF und DFT-Niveau praktisch berechnet werden. Die Bader-Methode bildet über die erste und zweite Ableitung der Elektronendichte nach den Raumkoordinaten einen Zusammenhang mit intuitiven Vorstellungen wie chemischen Bindungen.

Literatur

• M. P. Allen, D. J. Tildesly: Computer Simulation of Liquids. Oxford University Press, 1989, ISBN 0198556454
• P. W. Atkins, R. S. Friedman: Molecular Quantum Mechanics. 4. Aufl., Oxford University Press, Oxford 2004, ISBN 0199274983.
• C. J. Cramer Essentials of Computational Chemistry, Wiley, Chichester 2002, ISBN 0471485527.
• F. Jensen: Introduction to Computational Chemistry. John Wiley & Sons, Chichester 1999, ISBN 9780471984252.
• W. Kutzelnigg: Einführung in die Theoretische Chemie. Wiley-VCH, Weinheim 2002, ISBN 3527306099.
• A. R. Leach Molecular Modelling. Principles and Applications. 2. Aufl., Pearson Prentice Hall, Harlow 2001, ISBN 0582382106.
• E. Lewars: Computational Chemistry. Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Kluwer Academic Publishers, New York, Boston, Dordrecht, London, Moscow, 2004. ISBN 1-4020-7285-6. E-Book ISBN 0-306-48391-2
• J. Reinhold: Quantentheorie der Moleküle. 3. Aufl., Teubner, 2006, ISBN 3835100378.
• A. Szabo, N. S. Ostlund: Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. McGraw-Hill, 1989, ISBN 0-07-062739-8

Siehe auch

• Quantenchemie
• Kategorie:Theoretischer Chemiker

Weblinks

• lectures4you.de: Zusammenstellung von frei zugänglichem Online-Lehrmaterial zur Theoretischen Chemie

Teilbereiche der Chemie

Anorganische Chemie · Biochemie · Organische Chemie · Physikalische Chemie · Technische Chemie

---

Agrochemie · Analytische Chemie · Bioanorganische Chemie · Bioorganische Chemie · Biophysikalische Chemie · Chemoinformatik · Chemometrik · Elektrochemie · Geochemie · Kernchemie · Klinische Chemie · Kohlechemie · Kolloidchemie · Kombinatorische Chemie · Kosmochemie · Lebensmittelchemie · Magnetochemie · Medizinische Chemie · Meereschemie · Naturstoffchemie · Oberflächenchemie · Organometallchemie · Petrochemie · Pharmazeutische Chemie · Photochemie · Physikalische Organische Chemie · Polymerchemie · Radiochemie · Supramolekulare Chemie · Stereochemie · Theoretische Chemie · Thermochemie · Umweltchemie