Logischer Fehlschluss

Dieser Artikel wurde in der Qualitätssicherung Philosophie eingetragen. Dabei werden Artikel gelöscht, die nach Fristablauf sich als nicht relevant herausstellen oder kein akzeptables Niveau erreicht haben. Bitte hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion! Bitte entferne diesen Hinweis nicht ohne Absprache!

Als Fehlschluss oder Trugschluss (lat. fallacia) bezeichnet man einen Schluss, bei dem die abgeleitete Aussage nicht aus den explizit angegebenen oder implizit angenommenen Voraussetzungen folgt. Dies bedeutet nicht sofort, dass die abgeleitete Aussage auch falsch ist: Ein Fehlschluss gibt keinerlei Aufschluss über den tatsächlichen Wahrheitsgehalt der abgeleiteten Aussage.

Ein mit Absicht herbeigeführter Fehlschluss wird auch als Sophismus bezeichnet, ein unbeabsichtigter Fehlschluss wird auch Paralogismus genannt.

Beispiele

Um das Problem eines Fehlschlusses zu verdeutlichen, einige Beispiele:

Mangelnde Ursächlichkeit - reines gleichzeitiges Auftreten gibt noch keinen Grund - 'unechte', nicht kausale Korrelation

(vgl. auch: cum hoc ergo propter hoc)

Tatsache 1: England ist tollwutfrei.

Tatsache 2: Es gibt in England auch keine Störche.

Schlussfolgerung: Störche verursachen somit die Tollwut.

Bei Kenntnis der wirklichen Ursache für die Tollwutverbreitung handelt es sich bei diesem Fehlschluss um einen Sophismus, ansonsten um einen durch Unkenntnis herbeigeführten Paralogismus.

Derselbe Fehlschluss kann auch so dargestellt werden:

Tatsache 1: Patient XY hat Rückenschmerzen.

Tatsache 2: Patient XY hat einen Bandscheibenvorfall.

Schlussfolgerung: Der Bandscheibenvorfall ist die Ursache für die Rückenschmerzen.

Beide Schlüsse sind keine deduktiven (zwingenden, wahrheitskonservierenden) Schlussfolgerungen. Im besten Fall kann die Verknüpfung zweier Tatsachen eine Hypothese über einen Zusammenhang liefern, die mit wissenschaftlichen Methoden weiter geprüft werden muss. Wenn man die Formulierung einer solchen Hypothese als logische Schlussfolgerung ansehen möchte (was manche Logiker tun), so spricht man hier von einer Abduktion.

Zusammenhang zur Statistik

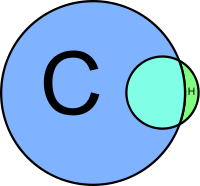
Cannabis wird manchmal als Einstiegsdroge für Heroin bezeichnet. Zwischen beiden Konsumentengruppen gibt es tatsächlich eine Überschneidung (in der Abbildung türkis): Die meisten Heroinbenutzer (kleinere Fläche H) waren vorher Cannabiskonsumenten (große Fläche C). Lässt sich daraus folgern, dass die Mehrheit der Cannabiskonsumenten später auf Heroin umsteigen wird?

Gerd Gigerenzer verweist darauf, dass die Mehrheit der Cannabisbenutzer an Heroin kein Interesse hat (verbleibender Rest der großen Fläche). Die Aussage Aus „die meisten Heroinbenutzer waren früher Cannabisbenutzer“ folgt „die meisten Cannabisbenutzer werden Heroinbenutzer sein“ ist ein Fehlschluss. Für Gigerenzer sind logische Fehlschlüsse ein Teil des „mathematischen Analphabetismus“.

Mathematik

In der Mathematik entstehen Fehlschlüsse oft bei falscher Anwendung von Rechenregeln, z. B. bei versehentlicher Division durch null:

Aus der wahren Aussage 2·0 = 1·0 könnte man mittels einer (genau deshalb nicht definierten) Division durch 0 die falsche Aussage 2 = 1 ableiten.

oder bei Anwendung der von den positiven reellen Zahlen her bekannten Gesetze des Wurzelziehens auf komplexe Zahlen:

Egal wie man „die“ Quadratwurzel einer komplexen Zahl definierte, es würden stets einige Wurzelgesetze gebrochen werden, z. B. gilt die Gleichung 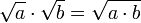$\sqrt{a}\cdot\sqrt{b}=\sqrt{a\cdot b}$ nicht immer. Man betrachtet daher stets beide Quadratwurzeln gleichzeitig.

Traditionelle Logik

In der Tradition der Logik wurden nicht nur die gültigen Schlussfolgerungen untersucht, sondern auch logische Fehlschlüsse im Rahmen der bis Ende des 19. Jahrhunderts üblichen Syllogistik betrachtet und kategorisiert.

Quaternio Terminorum

(lat. Vierheit der Begriffe)

Im kategorischen Syllogismus müssen genau drei verschiedene Begriffe vorkommen, jeder zweimal:

• Im Obersatz (= erste Prämisse) Prädikat und Mittelbegriff
• Im Untersatz (= zweite Prämisse) Subjekt und Mittelbegriff
• Im Schlusssatz (= Konklusion) Subjekt und Prädikat.

Wird diese Regel verletzt, ist ein Fehlschluss die Folge. Leicht zu entdecken ist er in folgendem Beispiel:

Schlüssel haben Bärte. Bärte kann man rasieren. Schlüssel kann man rasieren.

(Schlüsselbart und Barthaar)

Schwerer zu entdecken ist der Fehlschluss in diesem Beispiel:

Alle Erwachsenen lieben Kinder. Alle Kinder lieben Schokolade. Alle Erwachsenen lieben Schokolade.

In diesem Syllogismus kommen tatsächlich vier Begriffe vor, denn korrekt formuliert (zwei kategorische Urteile) müssten die Prämissen lauten:

Alle Erwachsenen sind Kinderlieber. Alle Kinder sind Schokoladenlieber. Es folgt: nichts.

Weitere Beispiele: Der Sophismus vom Verhüllten und der Sophismus vom Gehörnten von Eubulides:

Was du nicht verloren hast, das hast du noch. Hörner hast du nicht verloren. Daraus folgt: Du hast Hörner.

Erkennst Du diesen Verhüllten? Nein! Es ist Dein Vater! Daraus folgt: Du erkennst Deinen Vater nicht.

Quaternio-Terminorum-Fehlschlüsse beruhen oft auf der Homonymie zweier Begriffe, wie in diesem antiken Beispiel:

Die vom Kranken eingenommene Arznei ist gut. Je mehr Gutes man tut, desto besser ist es. Daraus folgt: Man muss möglichst viel Arznei einnehmen.

Weblink: [1]

Nicht distribuiertes Subjekt

Wenn im Schlusssatz eines Syllogismus das syllogistische Subjekt distribuiert ist, das heißt wenn über alle Mitglieder der vom Subjekt bezeichneten Klasse ein Urteil gefällt wird (z.B. „Alle S sind P“, „Keine S sind P“), dann muss auch der Untersatz (2. Prämisse, in der das Subjekt der Konklusion eingeführt wird) ein Urteil über alle Klassen-Mitglieder sein. Fehlschlüsse entstehen, wenn in der zweiten Prämisse nur eine Teilmenge des Subjekts gemeint ist, die Konklusion sich aber auf alle Elemente der Kategorie bezieht. Leicht zu entdecken ist der Fehlschluß in diesem Beispiel:

Alle Vegetarier sind gesund. Einige Menschen sind Vegetarier. Fehlschluss: Alle Menschen sind gesund.

Schwerer zu entdecken ist dieser Fehlschluss im folgenden Beispiel:

Omnivoren essen Fleisch. Menschen sind Omnivoren. Fehlschluss: Alle Menschen essen Fleisch.

Während im Schlusssatz alle lebenden Menschen gemeint sind, sind die 'Menschen' im Untersatz nur die Vertreter des biologischen Gattungsbegriffes, die also nur die 'Veranlagung' zum Omnivoren haben. Weblink: [2]

Nicht distribuierter Mittelbegriff

auch Sophismus des kollektiven Mittelbegriffs (lat. non distributivi, sed collectivi medii)

In einem gültigen Syllogismus ist der Mittelbegriff in mindestens einer Prämisse distribuiert. Ist er es nicht, kann ein Fehlschluss wie der folgende auftreten:

Alle Menschen sind Zweibeiner. Einige Zweibeiner sind Vögel. Fehlschluss: Einige Menschen sind Vögel.

Fehlschluss in der Kriminalistik

Das Ergebnis eines DNA-Tests, eines Fingerabdrucks oder einer sonstigen Spur alleine kann nicht über Schuld oder Nichtschuld eines Verdächtigen entscheiden. Es wird nur als Indiz gewertet, das durch weitere ergänzt werden muss. Viele Verdächtige legen allerdings ein Geständnis ab, wenn man sie mit dem Ergebnis konfrontiert.

Ist das nicht der Fall, muss das Ergebnis interpretiert werden, wobei Fehlschlüsse nicht auszuschließen sind. Eine ungültige Schlussfolgerung macht alle nachfolgenden ungültig:

1. Falsche Übereinstimmung durch falsch positive Testergebnisse
2. Bei einer zufälligen Übereinstimmung muss der Verdächtigte nicht der Urheber der Spur sein
3. Das biologische Material kann von jemand anderem hinterlegt worden sein
4. Das biologische Material muss nicht zum Tatzeitpunkt hinterlegt worden sein

     ----------      ----------      ----------      ----------      ----------
    |berichtete|    |tatsächl. |    |Urheber   |    |am Tatort |    |schuldig  |
    |Überein-  | →  |Überein-  | →  |          | →  |anwesend  | →  |          |
    | stimmung | 1  |stimmung  | 2  |          |  3 |          | 4  |          |
     ----------      ----------      ----------      ----------      ----------
      | |                                ^                                 ^
      | `--------------------------------´                                 | 
      | Urhebertrugschluss                                                 |
      |                                                                    |
      `-------------------------------------------------------------------´
        Trugschluss des Anklägers

Der Trugschluss des Anklägers (Gigerenzer 2002) besteht in der falschen (!) Annahme: P(Unschuld|Übereinstimmung) sei P(Übereinstimmung|Unschuld), wobei P für die bedingte Wahrscheinlichkeit steht.

Beim Trugschluss des Anklägers wird die Folgekette von Schlüssen also einfach übersprungen (siehe Beispiel unten) und die Wahrscheinlichkeit der Schuld wird übertrieben.

So wird auch oft in den Medien berichtet: da beide Proben mit einer Wahrscheinlichkeit von eins zu einer Million zufällig übereinstimmen, ist auch die Wahrscheinlichkeit der Unschuld eins zu einer Million, oder die Wahrscheinlichkeit der Schuld eine Million zu eins. Dies ist ein Fehlschluss und falsch (siehe auch bedingte Wahrscheinlichkeit). Genauso falsch ist die Formulierung: dass das Blut (am Tatort) von einer anderen Person als dem Verdächtigen stammt ist 1 zu eine Million, hier wird fälschlich eine Urheberwahrscheinlichkeit („Urhebertrugschluss“) angegeben - die Spur könnte auch „gelegt“ worden sein.

Damit von einer Übereinstimmung auf eine Urheberschaftwahrscheinlicheit geschlossen werden kann (Punkt 2), muss ein Kreis von Menschen gefunden werden, der objektiv in Frage kommt - vor Gericht wird eine subjektive A-Priori-Wahrscheinlichkeit nicht akzeptiert. Dieses prinzipielle Problem taucht sowohl bei einer gerichtlichen Untersuchung („Täterkreis“) als auch bei einem Vaterschaftstest auf.

Zeitlicher Zusammenhang von Ereignissen

Cum hoc ergo propter hoc (lat. „mit diesem, also wegen dieses“) bezeichnet einen logischen Fehler, bei dem zwei gemeinsam auftretende Ereignisse als Ursache und Wirkung erklärt werden. Auch Post hoc, ergo procter hoc -das Ereignis A zeitlich vor B- beweist keine Kausalität: der Tag folgt stets auf die Nacht, aber nicht, weil diese die Ursache für jenen ist. Möglicherweise ist A eine notwendige, aber keine hinreichende Bedingung von B. Inwieweit dies gilt, war Gegenstand der Untersuchung von David Hume und Immanuel Kant. Wenn etwa eine Billardkugel eine andere trifft, so sieht man von außen nichts als den zeitlichen Zusammenhang zwischen Auftreffen der ersten und Geschwindigkeitsänderung der zweiten. Laut Kant darf unter Einbeziehung (und nur dann) der Newton'schen Gesetze hier allerdings (Hume bestreitet es) sehr wohl eine Kausalität angenommen werden.

Räumlicher Zusammenhang von Ereignissen

Dies ist ein Sonderfall von Cum hoc ergo propter hoc: Aus der räumlichen Nähe zweier Ereignisse wird (logisch falsch, nur plausibel) auf eine Ursache für diese Nähe geschlossen. So wählte Peirce folgendes Beispiel für eine Abduktion (s. Beweis (Logik)): Jemand findet einige weiße Bohnen und daneben einen Sack voller weißer Bohnen. Er schließt: Die Bohnen stammen aus dem Sack. Aus der Gestaltpsychologie kennt man das Gesetz der Nähe: Elemente mit geringen Abständen voneinander werden als zusammengehörig wahrgenommen.

Siehe auch

• Naturalistischer Fehlschluss, intentionaler Fehlschluss, affektiver Fehlschluss, hermeneutischer Zirkel, Fallacia accidentalis, Humes Gesetz
• Fehlschluss, deskriptivistischer (auf John Langshaw Austin zurück gehend)
• Denkstil-Artefakt
• Falsch positiv, Metawissenschaft
• Negation, Polarität (Philosophie)
• These, Deduktion, Induktion (Denken), Abduktion (Wissenschaftstheorie), Statistik, Nullhypothese, Rhetorik, Dialektik, Fehler 1. und 2. Art, Falsche Beweisführung
• Ab uno disce omnes, A nescire ad non esse, Aequat causa effectum, Fallacia fictae necessitatis
• Kreisschluss
• Strohmann-Argument
• Paradoxon
• Stage migration
• Ökologischer Fehlschluss

Literatur

• Gerd Gigerenzer: Das Einmaleins der Skepsis. Über den richtigen Umgang mit Zahlen und Risiken. Berlin Verlag, ISBN 3-82700-079-3
• Arthur Schopenhauer: Ü. d. vierfache Wurzel des Satzes vom zureichenden Grunde, 1813
• Friedrich Überweg: System der Logik, § 126
• Rudolf Eisler: Wörterbuch der philosophischen Begriffe 1904
• Friedrich Kirchner: Wörterbuch der philosophischen Grundbegriffe 1907
• Charles Leonard Hamblin: Fallacies. London: Methuen 1970, ISBN 0416145701 (gebundene Ausgabe), ISBN 0-416-70070-5 (Taschenbuchausgabe) – ein Standardwerk zum Thema der Fehlschlüsse, in englischer Sprache

Weblinks

• Leo Groarke: „Informal Logic“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Bradley Dowden: „Fallacies“ in der Internet Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Timm Grams: Denkfallen und Paradoxa
• Gary N. Curtis: Fallacy Files (englisch)