- Quasitonneliert
-
Tonnelierte Räume sind spezielle lokalkonvexe Vektorräume, in denen der Satz von Banach-Steinhaus gilt. Diese Räume lassen sich durch ihre Nullumgebungsbasen charakterisieren.
Inhaltsverzeichnis
Motivation
Eine Tonne ist eine Teilmenge T eines lokalkonvexen K-Vektorraums E mit folgenden drei Eigenschaften
- T ist absolutkonvex, d.h. für
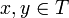 und
und 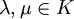 mit
mit 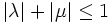 gilt
gilt 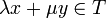 .
. - T ist abgeschlossen in der Topologie auf E.
- T ist absorbierend, d.h. zu jedem
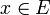 gibt es ein
gibt es ein 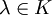 mit
mit 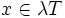 .
.
Leicht zeigt man, dass jeder lokalkonvexe Raum eine Nullumgebungsbasis aus Tonnen besitzt. Ist umgekehrt jede Tonne eine Nullumgebung, so nennt man den Raum tonneliert. Diese Bezeichnung geht auf Bourbaki zurück (französisch tonnelé, englisch barrelled).
Beispiele
- Jeder Fréchet-Raum (insbesondere also jeder Banachraum) ist tonneliert. Ist nämlich T eine Tonne im Fréchet-Raum E, so gilt
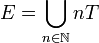 , da T absorbierend ist. Weil T abgeschlossen ist, folgt aus dem Satz von Baire, dass ein nT und damit T einen inneren Punkt hat. Aus der Absolutkonvexheit von T ergibt sich nun leicht, dass T eine Nullumgebung ist.
, da T absorbierend ist. Weil T abgeschlossen ist, folgt aus dem Satz von Baire, dass ein nT und damit T einen inneren Punkt hat. Aus der Absolutkonvexheit von T ergibt sich nun leicht, dass T eine Nullumgebung ist.
- Ist E ein Fréchet-Raum ungleich {0}, so ist
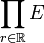 mit der Produkttopologie ein Beispiel für einen tonnelierten Raum, der nicht Fréchet-Raum ist.
mit der Produkttopologie ein Beispiel für einen tonnelierten Raum, der nicht Fréchet-Raum ist.
Vererbungseigenschaften
Quotientenräume nach abgeschlossenen Teilräumen, Produkträume und induktive Limitien tonnelierter Räume sind wieder tonneliert.
Die Tonneliertheit vererbt sich im Allgemeinen nicht auf abgeschlossene Unterräume oder projektive Limiten.
Der Satz von Banach-Steinhaus
Eine Menge B in einem lokalkonvexen Raum E heißt bekanntlich beschränkt, wenn sie von jeder Nullumgebung absorbiert wird, d.h. zu jeder Nullumbegung U von E gibt es ein λ > 0 mit
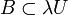 . Eine Familie
. Eine Familie 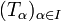 stetiger linearer Operatoren zwischen lokalkonvexen Vektorräumen E und F heißt gleichgradig stetig, wenn es zu jeder Nullumgebung V in F eine Nullumgebung U in E gibt, so dass
stetiger linearer Operatoren zwischen lokalkonvexen Vektorräumen E und F heißt gleichgradig stetig, wenn es zu jeder Nullumgebung V in F eine Nullumgebung U in E gibt, so dass 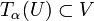 für alle
für alle 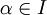 . Der folgende Satz kennzeichnet die tonnelierten Räume als diejenigen, in denen der Satz von Banach-Steinhaus gilt:
. Der folgende Satz kennzeichnet die tonnelierten Räume als diejenigen, in denen der Satz von Banach-Steinhaus gilt:Für einen lokalkonvexen Raum E sind äquivalent:
- E ist ein tonnelierter Raum.
- Ist F ein weiterer lokalkonvexer Raum und
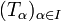 eine Familie stetiger linearer Operatoren
eine Familie stetiger linearer Operatoren 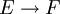 , die punktweise beschränkt ist (d.h. für jedes
, die punktweise beschränkt ist (d.h. für jedes 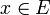 ist
ist 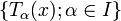 beschränkt), so ist
beschränkt), so ist 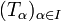 gleichgradig stetig.
gleichgradig stetig.
Beziehung zur Reflexivität
Ist E ein lokalkonvexer Vektorraum, so definiert jede beschränkte Menge B in E eine Halbnorm PB auf dem Dualraum
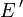 , indem man
, indem man 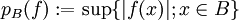 setzt. Versehen mit der Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, wird
setzt. Versehen mit der Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, wird 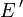 zu einem lokalkonvexen Vektorraum, den man dann mit Eb' bezeichnet. Dies verallgemeinert die Dualraumbildung bei normierten Räumen. Wie dort hat man eine natürliche Einbettung
zu einem lokalkonvexen Vektorraum, den man dann mit Eb' bezeichnet. Dies verallgemeinert die Dualraumbildung bei normierten Räumen. Wie dort hat man eine natürliche Einbettung 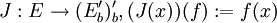 , und wie üblich identifiziert man E mit J(E), so dass E als Unterraum des Biduals (Eb')b' aufgefasst werden kann. Ist J surjektiv, so nennt man E halbreflexiv. Dann stimmen E und (Eb')b' zwar als Mengen überein, aber im Allgemeinen sind die lokalkonvexen Topologien auf E und dem Bidual (Eb')b' verschieden. Stimmen auch die Topolgien überein, so nennt man E reflexiv. Die Tonneliertheit ist genau die Eigenschaft, die einem halbreflexiven Raum zur Reflexivität fehlt, denn es gilt:
, und wie üblich identifiziert man E mit J(E), so dass E als Unterraum des Biduals (Eb')b' aufgefasst werden kann. Ist J surjektiv, so nennt man E halbreflexiv. Dann stimmen E und (Eb')b' zwar als Mengen überein, aber im Allgemeinen sind die lokalkonvexen Topologien auf E und dem Bidual (Eb')b' verschieden. Stimmen auch die Topolgien überein, so nennt man E reflexiv. Die Tonneliertheit ist genau die Eigenschaft, die einem halbreflexiven Raum zur Reflexivität fehlt, denn es gilt:Für einen lokalkonvexen Raum E äquivalent:
- E ist reflexiv
- E ist halbreflexiv und tonneliert.
Quasitonnelierte Räume
Man nennt eine Menge T in einem lokalkonvexen Raum bornivor, wenn sie jede beschränkte Menge absorbiert, d.h. wenn es zu jeder beschränkten Menge B ein
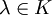 mit
mit 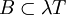 gibt. (Zur Wortherkunft vergleiche carnivor oder herbivor.)
gibt. (Zur Wortherkunft vergleiche carnivor oder herbivor.)Ein Raum heißt quasitonneliert, wenn jede bornivore Tonne eine Nullumgebung ist. Offensichtlich handelt es sich um eine Abschwächung der Tonneliertheit, Bornologische Räume sind quasitonneliert.
Die Quasitonneliertheit ist bei obiger Charakterisierung der Reflexivität ausreichend, denn für einen lokalkonvexen Raum E sind äquivalent:
- E ist reflexiv
- E ist halbreflexiv und tonneliert.
- E ist halbreflexiv und quasitonneliert.
Quellen
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
- T ist absolutkonvex, d.h. für
Wikimedia Foundation.
