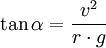Velofahren

Die Artikel Radfahrer, Fahrrad und Fahrradfahren überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Mediocrity 17:09, 1. Dez. 2008 (CET)

Radfahrer in Wien

Jan Ullrich in Kurvenhaltung (Druck auf dem Außenpedal und der inneren Hand)

Radrennfahrer nahe Aviano in Italien

Fahrradkurier in London

Der Ausdruck Fahrradfahren – auch Radfahren – bezeichnet die Fortbewegung auf einem nicht-motorisierten Zweirad, dem Fahrrad. Der Ausdruck bezeichnet auch die Sportart Fahrradfahren, die als Freizeitbeschäftigung, zur Erhaltung der Gesundheit oder als sportlicher Wettkampf (Leistungssport) betrieben wird.

Das Fahrrad befindet sich im labilen Gleichgewicht. Entgegen landläufiger Meinung ist dies zwar auch bei einem vierrädrigen Fahrzeug der Fall, jedoch ist die Auflagefläche hier wesentlich größer, zum Kippen muss der Schwerpunkt bei einem vierrädrigen Fahrzeug zunächst erheblich angehoben werden, was beim Fahrrad wegen der Rundung der Reifen so gut wie nicht der Fall ist.

Dass das Fahrradfahren trotzdem auch einem Menschen mit durchschnittlicher Fähigkeit sich bzw. ein System, dessen Teil er ist, auszubanlancieren möglich ist, liegt daran, dass die Eigenschaften des Fahrrades den Fahrer dabei unterstützen. Ein nachhaltiges Gleichgewicht des Systems Fahrrad/Fahrer beruht bei schnellerer Fahrt zu einem Teil auf der Fähigkeit des Fahrers, es durch kleine, habitualisierte Korrekturbewegungen auszubalancieren, zum anderen auf der Fahrradkonstruktion und verschiedenen physikalischen Effekten. Sie unterstützen ihn, so dass sogar ein freihändiges Fahren möglich ist.

Das Fahrrad im labilen Gleichgewicht

Ein Fahrrad berührt den Boden an zwei Stellen – den Auflageflächen der Reifen. Eine auch nur geringe Neigung der senkrecht zur Fahrbahn stehenden Rahmenebene führt beim stehenden Fahrrad zum Umkippen. Sobald der Schwerpunkt nicht mehr über der die Auflageflächen umfassenden und verbindenden Unterstützungsfläche liegt, kippt das Rad um.

Durch extremes Einschlagen des Lenkers lässt sich die Unterstützungsfläche für den Schwerpunkt vergrößern. Nur geübte Menschen können auf einem stehenden Fahrrad für längere Zeit einen Sturz vermeiden. Da diese Probleme beim Geradeausfahren nicht bestehen, muss die Fahrdynamik dafür ausschlaggebend sein.

Das dynamische Gleichgewicht

Einem Umkippen in eine Richtung während der Fahrt wird dadurch entgegengewirkt, dass der Lenker in die gleiche Richtung ausschlägt, eine kurze Kurve einleitet und nun durch die Zentrifugalkraft zur anderen Seite aufgerichtet wird. Dabei lässt sich ein Überkippen kaum vermeiden, der Lenker muss wiederum in die andere Richtung gelenkt werden und so weiter.

Eine Geradeausfahrt kommt daher einem kaum merkbaren Pendeln um die Gleichgewichtslage zwischen Kippen und Wiederaufrichten gleich. Bei langsamer Fahrt äußert sich das Pendeln durch starke, abwechselnde Lenkausschläge.

Bei freihändigem Fahren hilft das seitliche Neigen des Körpers zur Erzeugung eines entgegengesetzten Schweremoments. Freihändiges Fahren ist daher bei langsamer Fahrt nahezu unmöglich. Erst der weiter unten beschriebene Nachlauf und die Kreiselkräfte ermöglichen dies, indem sie bei einer Radneigung einen kontrollierbaren Lenkausschlag auslösen und so das Rad wieder in die gerade Fahrlinie zurückbringen, beziehungsweise eine stabile Kurvenfahrt ermöglichen.

Die Laufräder als Kreisel

Bei zunehmender Geschwindigkeit haben sowohl Lenkbewegungen als auch Körperschwerpunktverlagerungen (Balancieren) eine untergeordnete Bedeutung. Das gilt grundsätzlich für die Geradeausfahrt wie für Kurven. Ab einer Geschwindigkeit von 20 km/h werden die auf die Laufräder wirkenden Kreiselkräfte so stark, dass ein stabiles Geradeausfahren und ein großer Teil der Lenkmanöver auch freihändig möglich sind. Der Beitrag der rotierenden Laufräder als Kreisel zur Stabilisierung der Fahrt liegt darin, die zuvor geschilderten nötigen Lenkausschläge zu unterstützen bzw. beim Freihändigfahren auszulösen. Dadurch werden sowohl kleine, bei der Geradeausfahrt notwendige Korrekturen „automatisch“ ausgelöst als auch die länger aufrechtzuerhaltenden Lenkausschläge bei Kurvenfahrten.

Kreiseleffekte: Stabilisation und Präzession

Das Vorderrad stellt einen symmetrischen, nutationsfreien Kreisel dar; die Drehimpuls-, Rotations- und Figurenachsen sind identisch. Durch ein seitliches Neigen des Vorderrades wirkt ein Drehmoment, das senkrecht zum Drehimpuls steht. Dies führt zu einer Drehimpulsänderung und damit zu einer Präzessionsbewegung (s. auch Gyroskopischer Effekt bei Zweirädern): Der Lenker dreht sich in die Richtung der Neigung. Umgekehrt führt eine Drehung des Vorderrades um die Lenkachse zu einem Neigen des Fahrrades in die entgegengesetzte Richtung aufgrund der Präzession.

Das Hinterrad präzediert nicht, trägt aber zur Kreiselwirkung bei, indem seine Neigung auf das Vorderrad übertragen wird, was zu einer Verstärkung der Kreiselwirkung führt und das Rad insgesamt stabilisiert.

Der entscheidende Beitrag des Fahrers zur dauerhaften Erhaltung des Gleichgewichts

Wie Experimente bestätigen (s. u.), kann ein Fahrrad wie ein über eine Fläche gerollter, schmaler Autoreifen seine Geradeausfahrt ohne Fahrereinwirkung eine Weile beibehalten. Diese dem Fahrrad bzw. seinen Laufrädern innewohnende Eigenschaft lässt sich durch die Kreiselkräfte erklären. Bei einmaligem Auftreten von Störkräften und bei Verlangsamung der Geschwindigkeit nach einer bestimmten Zeit wird das Rad instabil, der gerollte Reifen beginnt zu taumeln und fällt schließlich um. Dies liegt überwiegend am Zeitverzug der Reaktion (s. o.: Präzession). Dadurch beginnen entgegengesetzte, rhythmische Neigungen und Drehungen, die aufschwingen und schließlich unkontrollierbar werden. Durch den Nachlauf (s. u.) wird die wechselseitige Verstärkung der Kräfte zwar gedämpft, aber es verbleibt ein entscheidender Rest an Instabilität.

Der Fahrer kann durch ein geschultes Gleichgewichtsempfinden, ein ruhiges Sitzen auf dem Sattel bzw. eine saubere Tretbewegung auch beim sportlichen Radfahren diese Instabilität in der Geradeausfahrt kompensieren. Bei der Kurvenfahrt unterstützt er die Stabilität durch seine Fahrtechnik (siehe Abschnitt Kurvenfahrt). Er bleibt die entscheidende Kraft – ohne ihn gerät jedes Fahrrad irgendwann aus der Kontrolle.

Experimente und Theorien zur Bedeutung der Kreiselkräfte

David E. H. Jones fand experimentell, dass mit Fahrer der Einfluss der Kreiselwirkungen bei normalen Geschwindigkeiten sehr klein sei, ohne Fahrer dagegen stabilisierten sie das angeschobene oder einen Hügel hinunterfahrende freilaufende Rad. Er montierte knapp oberhalb des Bodens ein drittes Laufrad neben das Vorderrad und drehte dieses in Rückwärtsrichtung, mit dem Ziel, die Kreiselwirkungen beider Vorderräder in etwa aufzuheben. Er konnte jedoch normal fahren, auch freihändig. Ohne Fahrer dagegen fiel das der Kreiselwirkungen beraubte Fahrrad auf der Stelle um. [1]

Felix Klein und Arnold Sommerfeld haben in ihrer Theorie des Kreisels eine erschöpfende theoretisch-analytische Abhandlung über die Kreiselwirkungen beim Fahrrad geliefert. Sie stellen fest, dass sich zwischen 16 und 20 km/h ein stabiler Bereich befindet, in dem allein die Kreiselwirkungen die Stabilisierung zu generieren vermögen, trotz der geringen Radmassen. Es ist dem Fahrer hier möglich, freihändig zu fahren. Unterhalb davon reicht der Lenkausschlag, den die Kreiselwirkung verursacht, nicht aus, um eine ausreichend große aufrichtende Zentrifugalkraft hervorzurufen; der Fahrer muss lenkend eingreifen. Fährt man sehr viel schneller, werden keine Kreiselwirkungen mehr spürbar. Die Hinterradspur nähert sich so schnell der Vorderradspur an, dass sich beide zusammen wie ein starres System verhalten. Das Fahrgefühl gleicht dem Fahren in einer schmalen Schiene; das Lenken und damit das Aufrechtbleiben ist erschwert.

Klein und Sommerfeld erkennen aber an, dass ein Fahrrad eher auf Energieersparnis und Leichtigkeit als auf Optimierung der Kreiselwirkungen konstruiert und durch die ausgleichenden Bewegungen eines Fahrers die Eigenstabilisierung „nicht gerade [..] erforderlich [..] ist“. Sie ziehen dennoch als Fazit, dass „[..] es doch kaum von der Hand zu weisen [ist], daß die Kreiselwirkungen zur Aufrechterhaltung des Gleichgewichts bei der Fahrt beitragen, wir möchten sagen, in besonders intelligenter Weise beitragen; sind sie es doch, die vermöge der Phase ihrer Wirkung zuerst ein Überfallen des Rades spüren und die dann die viel stärkeren, aber etwas langsamen Centrifugalwirkungen in den Dienst der Stabilität spannen.“ [2]

Kurvenfahrt

Eine Kurve wird nicht durch ein Lenken in die gewünschte Richtung eingeleitet. Laufradspuren auf Sand oder Schnee zeigen, dass zunächst eine leichte Lenkbewegung in die entgegengesetzte Richtung erfolgt. Schlüge man einfach nach links ein, bewegte sich die Auflagefläche des Reifens nach links unter dem Schwerpunkt weg, so dass die Schwerkraft ein Kippen nach rechts bewirken würde. Um die Kurve zu fahren, ist aber grundsätzlich eine Neigung in die gewünschte Kurvenrichtung, in diesem Falle nach links, notwendig.

Um das Rad in diese Schräglage zu bringen, muss es zunächst durch eine der gewünschten Richtung entgegengesetzte (kurze und leichte!) Lenkbewegung zum Kippen gebracht werden.

Bestimmung des Neigungswinkels

Eine Kurve kann als Teil einer Kreisbahn betrachtet werden. Legt sich der Fahrer in die Kurve, ist der Neigungswinkel, bei dem er nicht stürzt, abhängig von Fahrgeschwindigkeit und Kurvenradius. Je schneller die Fahrt und je enger die Kurve, desto größer muss der einzunehmende Neigungswinkel sein. Dieser ist eindeutig bestimmbar: Die Verbindungslinie zwischen Schwerpunkt und Unterstützungsfläche muss nämlich in Richtung der Resultierenden von Fliehkraft und Anziehungskraft verlaufen. Für den Neigungswinkel α zwischen der Resultierenden und der Senkrechten gilt daher:

$\tan \alpha = \frac{v^2}{r \cdot g}$

Dabei ist v die Geschwindigkeit, r der Kurvenradius und g die Schwerebeschleunigung, auf der Erde 9,81 m·s^–2.

Erwachsenen Menschen fällt das Erlernen des Fahrradfahrens häufig deshalb so schwer, weil die erforderliche Bewegungskoordination der Intuition entgegenläuft, auch wenn sie es von der Logik her schnell erfassen können.

Für einen ruhenden Beobachter wirkt auf das Fahrrad eine zum Kreismittelpunkt gerichtete Zentripetalkraft, die durch die Haftreibung der Laufräder aufgebracht wird. Der Haftreibungskoeffizient bestimmt nun den maximalen Neigungswinkel, dessen Überschreitung zum Wegrutschen des Vorderrades und zum Sturz führt. Vor engen Kurven und auf schmierigen, schotterigen oder glatten Bodenbelägen ist also ein Abbremsen notwendig, weil die Reibung sonst nicht ausreicht, eine der Fliehkraft betragsgleiche Zentripetalkraft aufzubringen.

Kreiselkräfte und Fahrereinfluss bei Kurvenfahrten

Wie schon beim Geradeausfahren, so sind es auch hier wieder die Kräfte der sich drehenden Laufräder, die die Fahrt durch Kurven entscheidend unterstützen. Haben die Räder durch die Präzession beim Kippen in der Geradeausfahrt einen Lenkeinschlag bewirkt, der korrigierend wirkte, so unterstützen sie nun den für die Kurvenfahrt notwendigen Einschlag des Vorderrades. Der Nachlauf (s.u.) dämpft diesen Einschlag, wobei kürzere Nachläufe bessere Kurveneigenschaften und schlechtere Geradeauslaufeigenschaften, größere Nachläufe die umgekehrten Eigenschaften bewirken.

Dem Fahrer ist auch hier die Feinabstimmung überlassen, ohne die eine kontrollierte Fahrt nicht möglich wäre. Beim sportlichen Radfahren (Radrennsport) sind zum erfolgreichen Durchfahren von Kurven weitere Techniken unerlässlich. Beispielsweise muss der Fahrer eine Körperspannung aufbauen, was durch Durchdrücken des fast gestreckten kurvenäußeren Beines (Pedale im tiefsten Punkt) bewirkt wird. Im Mountainbikesport hingegen, wo es eher um schnelle Verlagerung des Körperschwerpunktes aufgrund der Bodenbeschaffenheiten geht, hat sich eine Waagrechtstellung der Pedale als eher zweckmäßig erwiesen.

Überhöhung

Der Kurvenradius kann erheblich verkleinert werden, wenn die Fahrbahn nicht eben, sondern in Richtung Kurvenmittelpunkt geneigt ist (Überhöhung). Diese Hilfe machen sich sowohl Cyclo-Cross-Fahrer und Mountainbiker als auch Bahnfahrer zunutze:

• Im Cyclocross- und Mountainbike-Sport nutzt man z. B. ausgefurchte Kurven, die hierdurch eine Überhöhung aufweisen, um Kurven schneller zu durchfahren.
• Im Bahnradsport weisen die Radrennbahnen grundsätzlich in den Kurven Überhöhungen zwischen 30 Grad (lange Freiluft-Zementbahnen mit größerer Haftreibung) und gewöhnlich 45 Grad Überhöhungswinkel auf (in Ausnahmefällen sogar darüber: die nicht mehr existierenden Bahnen in Münster und Frankfurt am Main hatten Überhöhungen von über 55 Grad).

Ausweichmanöver

Bei Kurven, die im Zuge von kurzen Ausweichmanövern gefahren werden, ist die Technik des Gegenlenkens, um das Kippen einzuleiten, nicht notwendig, wenn der Fahrer anschließend die Fahrt auf der ursprünglichen Fahrlinie fortsetzen möchte. Statt der beschriebenen Technik lenkt der Fahrer das Fahrrad an dem Hindernis vorbei, während sein Körperschwerpunkt sich fast geradeaus weiterbewegt. Demzufolge ist diese Technik auch nur zum Ausweichen vor bodennahen Hindernissen, Schlaglöchern usw. geeignet. Wird sie in der falschen Situation angewandt, führt sie zu schweren Stürzen. Die Entscheidung über die Technik trifft der Fahrer nicht bewusst, sondern in Zehntelsekundenschnelle intuitiv.

Konstruktionsmerkmale eines Fahrrads, die das Fahren beeinflussen

Nachlauf und Radstand

Nachlauf

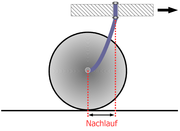
Als Nachlauf wird der Abstand zwischen dem Vorderradaufstandspunkt und dem Punkt, in dem die gedachte Verlängerung der Lenkachse den Boden trifft, dem so genannten Spurpunkt, bezeichnet. Geometrisch festgelegt wird der Nachlauf durch Laufradradius, Steuerkopfwinkel (zwischen Lenkachse und Boden) und der Gabelbiegung (senkrechter Abstand von Nabe zur Lenkachse). Der Name rührt daher, dass das Rad bei Lenkbewegungen dem Spurpunkt „hinterherläuft“. Ist der Nachlauf positiv, so befindet sich der Spurpunkt wie in der Abbildung dargestellt in Fahrtrichtung vor dem Aufsetzpunkt. Die Größe des Nachlaufs liegt meist zwischen 5 und 7,5 cm

Der Nachlauf ist wohl die wichtigste bauliche Unterstützung im Bemühen gegen das Umfallen während des Geradeausfahrens. Er wirkt auf folgende Arten:

1. Droht ein Sturz, bewirkt die bei Radneigung in der Vorderachse angreifende Schwerkraft des Vorderrades einen Lenkereinschlag in Richtung der Neigung. Wie oben beschrieben greift nun die Fliehkraft ein und richtet das Rad auf. Dieser Effekt ist gut sichtbar, hält man den Sattel fest und neigt das Rad. Prompt dreht sich das Vorderrad.

Nachlauf beim Einkaufswagen

2. Die Richtkraft versucht das Rad in Radflucht auszurichten. Anschaulich ist dieser Effekt bei Teewagen oder Einkaufswagen, deren Radachsen nicht unterhalb der Lenkachsen liegen, sodass ein Kräftepaar auftritt. Lagerkraft und Rollwiderstand (Reibung) lassen das Rad auf der Stelle verharren. Bewegt sich z. B. der Einkaufswagen, rotieren die Räder zunächst auf der Stelle. Erst wenn ein positiver Nachlauf erreicht ist, folgt das Rad der Bewegung hinterher. Ohne den Nachlauf wäre diese Richtkraft nicht vorhanden.

Ist der Nachlauf kurz, verhält sich das Fahrrad wendiger und bei niedrigen Geschwindigkeiten leichter steuerbar, hohe führen zu Rahmenflattern. Ein langer Nachlauf macht das Fahrrad richtungsstabiler, jedoch sind größere Lenkkräfte erforderlich und Langsamfahren ist schwieriger.

Dass ein Fahren mit einem negativen Nachlauf nur schwer möglich ist, zeigt das Experiment des Chemikers David E. H. Jones. Er versuchte im Jahr 1970 ein Fahrrad zu konstruieren, das unfahrbar ist. Die meisten entwickelten Radtypen waren jedoch mehr oder weniger trotzdem nutzbar. Erst ein Rad mit negativem Nachlauf war „sehr knifflig“ zu steuern und besaß vernachlässigbare Selbststabilisierung. [1]

Radstand

Radstand und Schwerpunktsweg

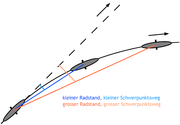
Ein Fahrrad mit zwei Laufrädern berührt den Boden in zwei Punkten. Der Abstand dieser Punkte heißt Radstand. In einer Kurve neigt sich das Rad in Kurvenrichtung, der Schwerpunkt wandert dabei in dieselbe Richtung. Je größer der Radstand, desto größer ist der Weg des Schwerpunkts bei der Gewichtsverlagerung und damit die Zeit, um die für eine Kurvenfahrt nötige Neigung zu erreichen. Das etwas träge Verhalten von Rädern mit langem Radstand, etwa Tandems, lässt sich hierdurch erklären.

Ein Fahrrad mit weit auseinanderstehenden Laufrädern ist weniger wendig, bleibt aber der Richtung treu. Mit nahe beieinanderstehenden Laufrädern reagiert es schneller auf Lenkbewegungen, dabei stellt sich aber ein eher nervöser Geradeauslauf ein. Seine Wendigkeit wird beim Rennrad genutzt.

Vor allem nicht betont sportlich konstruierte Fahrräder haben einen Radstand von deutlich über 1 m, ein Tandem gar 2 m. In Wettbewerben verwendete Rennräder weisen i.d.R. einen Radstand von 97–100 cm auf.

Um den Radstand zu messen, misst man die Entfernung der Radmittelpunkte (Nabenachsenmittelpunkt) bei geradeaus ausgerichtetem Lenker, die die gleiche Entfernung haben wie die Aufstehpunkte am Boden.

Laufradgröße und -gewicht

Je größer im Durchmesser und schwerer die Räder sind, desto größer sind die Kreiselmomente. Bei einem normalen Gebrauchsrad (Laufraddurchmesser 60 cm, Masse 1 kg) sind die Kreiselwirkungen etwa fünfmal so groß wie bei einem Kinderrad (30 cm; 0,4 kg). Korrekterweise hängt das Kreiselmoment natürlich nicht von der Masse des Laufrades sondern von der Verteilung der Masse im Laufrad ab; beispielsweise hat ein Laufrad mit einer „schweren“ Felge ein größeres Kreiselmoment als ein gleich schweres Laufrad mit einer „leichten“ Felge mit einer „schweren“ Nabenschaltung. Konstruiert werden Fahrräder aber eher unter dem Gesichtspunkt des Energiesparens und daher so leicht wie möglich.

Abrollfläche

Bei Geradeausfahrt entspricht die Form der Abrollfläche der Reifen einem Zylindermantel, bei einer Radneigung einem Kegel. Ein gerollter Kegel kreist um sein spitzes Ende. So ist ein Steuern durch Schräglage möglich, der Effekt ist jedoch gering.

Vorderradabsenkung

Einen sehr geringen Einfluss haben der Vorbau und Lenkkopf. In Geradeausstellung hat er die höchste Lage und damit größte potentielle Energie. Der Zustand niedrigster Energie wird angestrebt, daher werden Lenkeinschläge durch die Vorderradabsenkung verstärkt. Bei einem Lenkwinkel von 8° beträgt diese nur 0,15 mm.

Sitzposition

Verlagert der Fahrer sein Gewicht auf das Hinterrad, sind geringere Lenkkräfte nötig. Dies führt allerdings zu Übersteuern und flatterigem Fahrverhalten aufgrund zu weiter oder zu schneller Richtungskorrekturen. Beugt man sich vor und belastet das Vorderrad, sind größere Lenkkräfte nötig. Man untersteuert und erreicht ein schwankendes Fahrverhalten wegen zu später und geringer Korrekturen.

Als Erfahrungswert gilt, dass ein ausgewogenes Fahrverhalten gewährleistet ist, wenn 55 bis 60 % des Gesamtgewichts von Fahrrad und Fahrer auf dem Hinterrad lasten.

Gesetzliche Bestimmungen

Hier werden die rechtlichen Bestimmungen für das Radfahren beschrieben. Die gesetzlichen Regeln für das Fahrrad selbst, also beispielsweise die Ausrüstung mit Licht, Hupe etc. finden sich im Artikel Fahrrad#Gesetzliche Bestimmungen.

Österreich

• Nebeneinanderfahren: Grundsätzlich dürfen Radfahrer nur auf Radwegen und in Wohnstraßen sowie auf sonstigen Straßen mit öffentlichen Verkehr bei Trainingsfahrten mit Rennfahrrädern nebeneinander fahren. Beim Nebeneinanderfahren darf nur der äußerste rechte Fahrstreifen benutzt werden. Dies bedeutet in der Praxis - und ausgehend von der üblichen Fahrstreifenbreite - dass maximal zwei trainierende Radrennfahrer nebeneinander unterwegs sein dürfen.

• Fahren am Zebrastreifen: Radfahrer dürfen auf dem Zebrastreifen nicht fahren, das Schieben des Rades ist jedoch erlaubt.

• Fahren am Gehsteig: Radfahren am Gehsteig ist verboten, das Schieben ist erlaubt

• Pflicht zur Benutzung von Radwegen: Ist eine Radfahranlage (Radweg, Geh- und Radweg, Radfahrstreifen, Mehrzweckstreifen) vorhanden, so muss diese auch benutzt werden. Von der Benutzungspflicht (Wahlmöglichkeit) ausgenommen sind einspurige Fahrräder mit Anhängern, die unter 80 cm breit sind und Trainingsfahrten mit Rennfahrrädern. Weiter dürfen Fahrräder mit sonstigen Anhängern oder mehrspurige Fahrräder Radfahranlagen nicht benutzen.

• Fahrordnung auf Radfahranlagen: Grundsätzlich dürfen Radfahranlagen in beiden Richtungen befahren werden, sofern sich aus Bodenmarkierungen (Richtungspfeile) nichts anderes ergibt. Die Ausnahme hierbei ist der Radfahrstreifen, denn dieser darf - außer in Einbahnstraßen - nur in derselben Richtung wie der angrenzende Fahrstreifen befahren werden.

• Radfahrerüberfahrten: Radfahrerüberfahrten, wo der Verkehr nicht durch Arm- oder Lichtzeichen geregelt wird, dürfen Radfahrer nur mit einer Geschwindigkeit von höchstens 10 km/h und nicht unmittelbar vor einem herannahenden Fahrzeug und für dessen Lenker überraschend befahren.

• Fahren gegen eine Einbahnstraße: Das Fahren mit dem Rad gegen eine Einbahnstraße ist grundsätzlich verboten, allerdings kann dies durch Verordnung Radfahrern erlaubt werden. In Wohnstraßen, die auch Einbahnstraßen sind, ist das Fahren in die entgegengesetzte Richtung erlaubt.

• Vorschlängeln: Radfahrer dürfen sich vor Kreuzungen, Eisenbahnübergängen oder Straßenengen neben oder zwischen den angehaltenen Fahrzeugen vorschlängeln. Allerdings nur, wenn dafür ausreichend Platz vorhanden ist und Fahrzeuge dadurch nicht beim Einbiegen behindert werden. Trotzdem sollte man als Radler vorsichtig und mit angemessenem Tempo vorfahren, um auf plötzliche Situationen, wie beispielsweise das Öffnen einer Autotür, rasch reagieren zu können.

Andere Länder

Die gesetzliche Lage in anderen Ländern kann sich von jener im deutschsprachigen Raum zum Teil erheblich unterscheiden. So gilt beispielsweise in Spanien und Portugal die Rechtsregel nicht für Radfahrer: Hier hat der motorisierte Verkehr gegenüber Radfahrern immer Vorrang!

Literatur

• Michael Gressmann: Fahrradphysik und Biomechanik. Kiel: Moby Dick Verlag, 2002, ISBN 3-89595-023-8
• Frank Bollerey: Das Problem des Gleichgewichts beim Fahrradfahren aus physikalischer Sicht. Diplomarbeit, Universität Kassel, 1999
• Hans Joachim Schlichting: Zur Gleichgewichtsproblematik beim Fahrradfahren. In: technic-didact 9/4, S. 257, 1984. (Download 57kB pdf)
• Roger Erb: Zum Problem der Stabilität beim Fahrradfahren. In: MNU 5/54 (2001), 279–284. (Download 320kB pdf)
• [1] David E. H. Jones: The Stability of the Bicycle. In: Physics Today 23 (April 1970) S. 34–40. (Download 9MB pdf englisch)
• [2] Felix Klein, Arnold Sommerfeld: Über die Theorie des Kreisels. S. 863–884 (1897). Stuttgart: Teubner, 1965

Weblinks

• Fahrrad korrekt einstellen
• Fahrradphysik