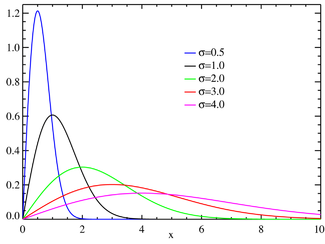
- Rayleigh-Verteilung
-
In der Wahrscheinlichkeitstheorie und Statistik wird mit Rayleighverteilung (nach John William Strutt, 3. Baron Rayleigh) eine kontinuierliche Wahrscheinlichkeitsverteilung bezeichnet.
Wenn die Komponenten eines zweidimensionalen Zufallsvektors normalverteilt und statistisch unabhängig sind, dann ist der Betrag Rayleigh-verteilt. Dies tritt zum Beispiel bei Quadraturamplitudenmodulation in Telekommunikationssystemen auf, wo die Sendesymbole durch einen Punkt in der komplexen Ebene dargestellt werden können.
Sind nun Abweichungen des Real- und Imaginärteils normal verteilt und statistisch unabhängig, so weist der Betrag der komplexen Zahl eine Rayleighverteilung auf.
Die Verteilung von 10-Minutenmittelwerten der Windgeschwindigkeit werden ebenfalls des Öfteren durch eine Rayleighverteilung beschrieben, wenn nicht eine zweiparametrige Weibull-Verteilung gewählt werden soll.
Inhaltsverzeichnis
Definition
Eine stetige Zufallsvariable X heißt Rayleigh-verteilt mit Parameter σ > 0, wenn sie die Wahrscheinlichkeitsdichte
besitzt. Daraus ergibt sich die Verteilungsfunktion
Eigenschaften
Momente
Die Momente beliebiger Ordnung können über folgende Formel errechnet werden:
wobei Γ(z) die Gammafunktion darstellt.
Erwartungswert
Der Erwartungswert ergibt sich zu
 .
.
Varianz
Die Varianz der Verteilung ist
 .
.
Somit ist das Verhältnis zwischen Erwartungswert und Standardabweichung bei dieser Verteilung konstant:
 .
.
Schiefe
Für die Schiefe erhält man
Wölbung (Kurtosis)
Die Wölbung ergibt sich zu
Charakteristische Funktion
Die Charakteristische Funktion ist
wobei
 die komplexe Fehlerfunktion ist.
die komplexe Fehlerfunktion ist.Momenterzeugende Funktion
Die Momenterzeugende Funktion ist gegeben durch
wobei
 wiederum die Fehlerfunktion ist.
wiederum die Fehlerfunktion ist.Modus
Das Maximum erreicht die Rayleigh-Verteilung für x = σ denn
für
 . Damit ist σ der Modus der Rayleigh-Verteilung.
. Damit ist σ der Modus der Rayleigh-Verteilung.Im Maximum hat f() den Wert
 .
.
Parameterschätzung
Die Maximum-Likelihood Schätzung von σ erfolgt über:
Beziehungen zu anderen Verteilungen
Die Chi-Verteilung, Weibull-Verteilung und Rice-Verteilung sind Verallgemeinerungen der Rayleighverteilung.
Beziehung zur Chi-Quadrat-Verteilung
Wenn R∼Rayleigh(1) dann ist R2 Chi-Quadrat verteilt mit zwei Freiheitsgraden:

Beziehung zur Weibull-Verteilung

Beziehung zur Exponentialverteilung
Wenn X exponentialverteilt ist
 , dann ist
, dann ist  .
.Beziehung zur Gammaverteilung
Wenn R∼Rayleigh(σ2) dann ist
 gammaverteilt mit den Parametern N und 2σ2:
gammaverteilt mit den Parametern N und 2σ2: ![[Y=\sum_{i=1}^N R_i^2] \sim \Gamma(N,2\sigma^2)](a/b2a73fb8d83427b643055fabc41f2f14.png) .
.Beziehung zur Normalverteilung
R∼Rayleigh(σ) ist Rayleigh verteilt, wenn
 wobei
wobei  und
und  zwei statistisch unabhängige Normalverteilungen sind.
zwei statistisch unabhängige Normalverteilungen sind.Siehe auch
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta
Wikimedia Foundation.