- Buchstabenhäufigkeit
-
Die Buchstabenhäufigkeit ist eine statistische Größe, die angibt, wie oft ein bestimmter Buchstabe in einem Text oder einer Sammlung von Texten („Korpus“) vorkommt. Sie kann als absolute Anzahl oder in Relation zur Gesamtzahl der Buchstaben des Textes angegeben werden. Die Häufigkeitsverteilung der Buchstaben hängt von der jeweiligen Sprache ab. Während frühere Annahmen pauschal die statistische Verteilung der Buchstabenhäufigkeit durch das Zipfsche Gesetz vorherzusagen glaubten, hat die quantitative Linguistik gezeigt, dass eine Reihe anderer Wahrscheinlichkeitsverteilungen [1] in Betracht zu ziehen sind (Best 2005). Zählungen zur Häufigkeit von Buchstaben oder Lauten in Texten oder Textkorpora sind spätestens seit dem frühen 19. Jahrhundert nachweisbar.[2] Für manche Zwecke ist es auch interessant, wie häufig ein Buchstabe am Wortanfang oder am Wortende vorkommt.
Inhaltsverzeichnis
Anwendung
Die Buchstabenhäufigkeit wird in der Entschlüsselung von Substitutionsverfahren in der Kryptoanalyse sowie in der Datenkompression und -kodierung benutzt. Bei einfachen Verschlüsselungsverfahren wie bei der Cäsarchiffre kann ein Text alleine durch Häufigkeitsanalyse entschlüsselt werden. Dabei werden die Häufigkeiten der einzelnen Zeichen im Geheimtext festgestellt, und dann mit der Häufigkeit der Zeichen in einem Klartext der vermuteten Sprache verglichen. Nun werden die Buchstaben des Geheimtextes durch die „normalen“ Buchstaben gleicher Häufigkeit ersetzt. Der häufigste Buchstabe des Geheimtextes entspricht dann zum Beispiel dem Klartextbuchstaben „e“. Diese Methode ist offensichtlich für längere zu entschlüsselnde Text besonders gut geeignet, weil die statistische Abweichung der gefundenen Buchstabenhäufigkeit von der zu erwartenden Häufigkeit geringer wird.
Für den Maschinenschreibunterricht ist es ungemein wichtig, dass die Lehrkraft über die Buchstabenhäufigkeit in einer Sprache gut informiert ist und die Unterrichtsinhalte entsprechend darauf abgestimmt werden. Häufige Buchstaben wie das E oder das I müssen hinreichend trainiert werden um eine möglichst hohe Anschlagszahl und eine gute Schreibsicherheit zu erzielen. Bei der Erstellung ergonomischer Tastaturbelegungen spielt die Buchstabenhäufigkeit ebenfalls eine große Rolle. Hersteller von Buchstabenspielen wie Boggle oder Scrabble berücksichtigen bei den nationalen Varianten ebenfalls die Häufigkeit und, falls vorhanden, auch die Wertigkeit der Buchstaben.
Eine der ersten Anwendungen war das Morse-Alphabet, das für häufige Zeichen kurze Codes verwendet (zum Beispiel E = ·); für selten gebrauchte Zeichen dagegen längere Codes (zum Beispiel Q = – – · –).
Siehe auch: Shannon-Fano-KodierungWeiterführung
Die Weiterführung der Buchstabenhäufigkeit ist die Häufigkeit von Buchstabenpaaren und -tripeln und die Worthäufigkeit. Befasst man sich statt mit der geschriebenen einmal mit der gesprochenen Sprache, so kann man ganz entsprechend auch Erhebungen zur Laut- oder Phonemhäufigkeit durchführen.
Buchstabenhäufigkeiten in deutschsprachigen Texten
Die Umlaute ä, ö und ü wurden wie ae, oe und ue gezählt, die Ligatur ſz als eigenständiges Zeichen ß.[3]
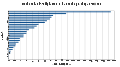
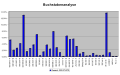
Platz Buchstabe Relative Häufigkeit 1. E 17,40 % 2. N 9,78 % 3. I 7,55 % 4. S 7,27 % 5. R 7,00 % 6. A 6,51 % 7. T 6,15 % 8. D 5,08 % 9. H 4,76 % 10. U 4,35 % 11. L 3,44 % 12. C 3,06 % 13. G 3,01 % 14. M 2,53 % 15. O 2,51 % 16. B 1,89 % 17. W 1,89 % 18. F 1,66 % 19. K 1,21 % 20. Z 1,13 % 21. P 0,79 % 22. V 0,67 % 23. ß 0,31 % 24. J 0,27 % 25. Y 0,04 % 26. X 0,03 % 27. Q 0,02 % Zum Vergleich: Bei einer Gleichverteilung der 27 Buchstaben betrüge die Häufigkeit jeweils 3,704 %.
Anfangsbuchstaben
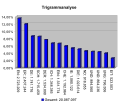
Die Häufigkeit von Anfangsbuchstaben gibt an, wie oft ein Buchstabe als erster Buchstabe eines Wortes vorkommt. Sie hängt relativ stark von der Textart ab. Für Fließtext sind die fünf häufigsten Anfangsbuchstaben:[4]
Platz Buchstabe Relative Häufigkeit 1. D 14,2 % 2. S 10,8 % 3. E 7,8 % 4. I 7,1 % 5. W 6,8 % Für Lexika ergibt sich eine andere Verteilung. Die Buchstaben „D“, „E“, „I“ und „W“ kommen im Vergleich zum Fließtext wesentlich seltener am Wortanfang vor, „S“ kommt mit deutlichem Abstand am häufigsten vor:[4]
Platz Buchstabe Relative Häufigkeit 1. S 11,8 % 2. K 7,3 % 3. A 7,1 % 4. P 7,0 % 5. B 5,7 % 6. M 5,7 % Endbuchstaben
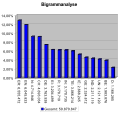
Die Häufigkeit von Endbuchstaben gibt an, wie häufig ein Buchstabe als letzter Buchstabe eines Wortes vorkommt. (Als Beispiel-Textbasis wurde das Buch Effi Briest von Theodor Fontane ausgewertet, wobei „ß“ stets als „ss“ gezählt wurde. Die Textbasis umfasst alle 36 Kapitel dieses Werks mit insgesamt 572.849 Zeichen.)
Platz Buchstabe Relative Häufigkeit 1. N 21,0 % 2. E 15,1 % 3. R 13,0 % 4. T 10,3 % 5. S 9,6 % Häufigkeitsdiagramme
-
Diagramm zu den relativen Buchstabenhäufigkeiten in deutschsprachigen Texten
-
Monogramm-Häufigkeitsgebirge: Die Buchstaben-Häufigkeitsverteilung eines längeren deutschen Textes.
-
Bigramm-Häufigkeitsgebirge: Verteilung der häufigsten Bigramme in einem deutschen Text.
-
Trigramm-Häufigkeitsgebirge: Verteilung der häufigsten Trigramme in einem deutschen Text. Die Tripel ER_ und EN_ sind am häufigsten („_“ steht für das Leerzeichen).
Buchstabenhäufigkeiten in ausgewählten Sprachen
Buchstabe Deutsch Englisch [5] Französisch [6] Spanisch [7] Esperanto [8] Italienisch[9] Schwedisch[10] a 6,51 % 8,167 % 7,636 % 12,53 % 12,12 % 11,74 % 9,3 % b 1,89 % 1,492 % 0,901 % 1,42 % 0,98 % 0,92 % 1,3 % c 3,06 % 2,782 % 3,260 % 4,68 % 0,78 % 4,5 % 1,3 % d 5,08 % 4,253 % 3,669 % 5,86 % 3,04 % 3,73 % 4,5 % e 17,40 % 12,702 % 14,715 % 13,68 % 8,99 % 11,79 % 9,9 % f 1,66 % 2,228 % 1,066 % 0,69 % 1,03 % 0,95 % 2,0 % g 3,01 % 2,015 % 0,866 % 1,01 % 1,17 % 1,64 % 3,3 % h 4,76 % 6,094 % 0,737 % 0,70 % 0,38 % 1,54 % 2,1 % i 7,55 % 6,966 % 7,529 % 6,25 % 10,01 % 11,28 % 5,1 % j 0,27 % 0,153 % 0,545 % 0,44 % 3,50 % 0,00 % 0,7% k 1,21 % 0,772 % 0,049 % 0,00 % 4,16 % 0,00 % 3,2 % l 3,44 % 4,025 % 5,456 % 4,97 % 6,14 % 6,51 % 5,2 % m 2,53 % 2,406 % 2,968 % 3,15 % 2,99 % 2,51 % 3,5 % n 9,78 % 6,749 % 7,095 % 6,71 % 7,96 % 6,88 % 8,8 % o 2,51 % 7,507 % 5,378 % 8,68 % 8,78 % 9,83 % 4,1 % p 0,79 % 1,929 % 3,021 % 2,51 % 2,74 % 3,05 % 1,7 % q 0,02 % 0,095 % 1,362 % 0,88 % 0,00 % 0,51 % 0,007 % r 7,00 % 5,987 % 6,553 % 6,87 % 5,91 % 6,37 % 8,3 % s 7,27 % 6,327 % 7,948 % 7,98 % 6,09 % 4,98 % 6,3 % t 6,15 % 9,056 % 7,244 % 4,63 % 5,27 % 5,62 % 8,7 % u 4,35 % 2,758 % 6,311 % 3,93 % 3,18 % 3,01 % 1,8 % v 0,67 % 0,978 % 1,628 % 0,90 % 1,90 % 2,10 % 2,4 % w 1,89 % 2,360 % 0,114 % 0,02 % 0,00 % 0,00 % 0,03 % x 0,03 % 0,150 % 0,387 % 0,22 % 0,00 % 0,00 % 0,1 % y 0,04 % 1,974 % 0,308 % 0,90 % 0,00 % 0,00 % 0,6 % z 1,13 % 0,074 % 0,136 % 0,52 % 0,50 % 0,49 % 0,02 % œ 0,00 % 0,00 % 0,018 % 0,00 % 0,00 % 0,00 % 0,00 % ß 0,31 % 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % à 0,00 % 0,00 % 0,486 % 0,00 % 0,00 % siehe a 0,00 % ç 0,00 % 0,00 % 0,085 % 0,00 % 0,00 % 0,00 % 0,00 % ĉ 0,00 % 0,00 % 0,00 % 0,00 % 0,66 % 0,00 % 0,00 % è 0,00 % 0,00 % 0,271 % 0,00 % 0,00 % siehe e 0,00 % é 0,00 % 0,00 % 1,904 % 0,00 % 0,00 % siehe e 0,00 % ê 0,00 % 0,00 % 0,225 % 0,00 % 0,00 % 0,00 % 0,00 % ë 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % ĝ 0,00 % 0,00 % 0,00 % 0,00 % 0,69 % 0,00 % 0,00 % ĥ 0,00 % 0,00 % 0,00 % 0,00 % 0,02 % 0,00 % 0,00 % î 0,00 % 0,00 % 0,045 % 0,00 % 0,00 % 0,00 % 0,00 % ì 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % siehe i 0,00 % ï 0,00 % 0,01 % 0,005 % 0,00 % 0,00 % 0,00 % 0,00 % ĵ 0,00 % 0,00 % 0,00 % 0,00 % 0,12 % 0,00 % 0,00 % ò 0,00 % 0,00 % 0,00 % 0,00 % 0,00 % siehe o 0,00 % ŝ 0,00 % 0,00 % 0,00 % 0,00 % 0,38 % 0,00 % 0,00 % ù 0,00 % 0,00 % 0,058 % 0,00 % 0,00 % siehe u 0,00 % ŭ 0,00 % 0,00 % 0,00 % 0,00 % 0,52 % 0,00 % 0,00 % Siehe auch
- Benfordsches Gesetz (Ziffernhäufigkeit)
- Häufigkeitsklasse
- Lauthäufigkeit
- Phonemhäufigkeit
- Worthäufigkeit
- N-Gramm
Literatur
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. Springer, Berlin u. a. 1995, ISBN 3-540-58118-9. Enthält Buchstabenhäufigkeiten im Deutschen und Englischen mit Prozentangaben S. 223.
- Karl-Heinz Best: Zur Häufigkeit von Buchstaben, Leerzeichen und anderen Schriftzeichen in deutschen Texten. In: Glottometrics. 11, 2005, ISSN 1617-8351, S. 9–31. Gibt neben den Buchstabenhäufigkeiten auch die Anteile anderer Zeichen in deutschen Texten an.
- Karl-Heinz Best: Buchstabenhäufigkeiten im Deutschen und Englischen. In: Naukovyj Visnyk Černivec'koho Universitetu. Vypusk 231, 2005, ZDB-ID 2390772-1, S. 119–127. Enthält unter anderem eine Übersicht über die Buchstabenhäufigkeiten in einem deutschen Briefkorpus von knapp 100000 Buchstaben.
- Erich Mater: Deutsche Verben. 1. Alphabetisches Verzeichnis. Bibliographisches Institut, Leipzig 1966. Enthält im Anfangskapitel eine Übersicht über die Häufigkeit von Anfangsbuchstaben in 6 verschiedenen Wörterbüchern sowie eine Gesamtübersicht. (Leider keine Seitenzählung).
- Helmut Meier: Deutsche Sprachstatistik. 2. erweiterte und verbesserte Auflage. Olms, Hildesheim 1967 (Olms Paperbacks 31). Buchstabenstatistik des Deutschen, Englischen und Spanischen S. 334.
- Gustav Muthmann: Rückläufiges deutsches Wörterbuch. Handbuch der Wortausgänge im Deutschen, mit Beachtung der Wort- und Lautstruktur. Niemeyer, Tübingen 1988, ISBN 3-484-31078-2 (Reihe germanistische Linguistik 78). Enthält S. 36 eine Zusammenstellung der Häufigkeiten von Anfangsbuchstaben sowie S. 65 der Endbuchstaben.
- Gustav Muthmann: Phonologisches Wörterbuch der deutschen Sprache. Niemeyer, Tübingen 1996, ISBN 3-484-31163-0, S. 35–37 (Reihe Germanistische Linguistik 163). Häufigkeit von Graphemen und Phonemen.
- Wolfgang Schönpflug: n-Gramm-Häufigkeit in der deutschen Sprache. I. Monogramme und Digramme. In: Zeitschrift für experimentelle und angewandte Psychologie. 16, 1969, ISSN 0044-2712, S. 157–183. Enthält S. 162f. eine Übersicht über die Häufigkeit von Buchstaben in einem Textkorpus von über 100000 Wörtern Länge, getrennt nach der Position im Wort.
Weblinks
- Facharbeit zum Thema „Buchstabenhäufigkeit“ DE, FR, IT, PT, ES
- Java-Anwendung, die die Buchstabenhäufigkeit aus einer Textdatei ausliest
- Grazer Projekt zur Quantitativen Textanalyse (QuanTA)
- Bibliographien und weitere Informationen zum Göttinger Projekt Quantitative Linguistik
- Portables Freeware-Tool um die Häufigkeiten von Buchstaben und/oder Silben aus beliebig langen Texten zu bestimmen
Einzelnachweise
- ↑ S. dazu: http://lql.uni-trier.de//index.php/Phoneme_frequency; Buchstaben, Laute und Phoneme folgen im Prinzip den gleichen Verteilungen.
- ↑ Karl-Heinz Best: Laut- und Buchstabenzählungen im frühen 19. Jahrhundert. In: Glottometrics 20, 2010, S. 110-114.
- ↑ Albrecht Beutelspacher, Kryptologie, 7. Aufl., Wiesbaden: Vieweg Verlagsgesellschaft, 2005, ISBN 3-8348-0014-7, Seite 10
- ↑ a b Peter Vogelgesang, 2003: Häufigkeit von Buchstaben.
- ↑ English letter frequencies
- ↑ CorpusDeThomasTempé. Abgerufen am 15. Juni 2007.
- ↑ Fletcher Pratt, Secret and Urgent: the Story of Codes and Ciphers Blue Ribbon Books, 1939, pp. 254-255.
- ↑ La Oftecoj de la Esperantaj Literoj. Abgerufen am 14. September 2007.
- ↑ Simon Singh, Codici e Segreti, 1999, RCS, ISBN 88-17-12539-3
- ↑ Singh, Simon; Brogren Margareta: Kodboken: konsten att skapa sekretess - från det gamla Egypten till kvantkryptering, Norstedt, Stockholm 1999 (swe). ISBN 91-1-300708-4 (inb.).
Schlagen Sie auch in anderen Wörterbüchern nach:
Buchstabenhäufung — Die Buchstabenhäufigkeit ist eine statistische Größe, die angibt, wie oft ein bestimmter Buchstabe in einem Text bzw. einer Sammlung von Texten („Korpus“) vorkommt. Sie kann als absolute Anzahl oder in Relation zur Gesamtzahl der Buchstaben des… … Deutsch Wikipedia
ERNSTL — ETAOIN SHRDLU sind die ersten zwölf der am häufigsten genutzten Buchstaben der englischen Sprache. Dies ist leicht verschieden von der Buchstabenhäufigkeit in Wörterbucheinträgen. Die gesamte Sequenz ist ETAOIN SHRDLU CMFWYP VBGKQJ XZ. Drucksatz… … Deutsch Wikipedia
Häufigkeitsgebirge — Das deutsche Alphabet ist diejenige Variante des lateinischen Alphabets, die zur Schreibung der deutschen Sprache verwendet wird. Im heutigen standardisierten Gebrauch umfasst es die 26 Grundbuchstaben des lateinischen Alphabets zuzüglich der… … Deutsch Wikipedia
Informationsdichte — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Informationsentropie — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Maximale Entropie — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Maximalentropie — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Shannon-Entropie — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Shannonentropie — Entropie ist ein Maß für den mittleren Informationsgehalt oder auch Informationsdichte eines Zeichensystems. Der Begriff in der Informationstheorie ist in Analogie zur Entropie in der Thermodynamik und Statistischen Mechanik benannt. Beide… … Deutsch Wikipedia
Buchstaben — Ein Buchstabe ist ein Kommunikations Aufschreibzeichen, welches in einer menschlichen, alphabetischen Schriftsprache eine allgemeine Verwendung findet. Die Gesamtheit der verschiedenen Buchstaben einer phonembasierten Schriftsprache ergibt ein… … Deutsch Wikipedia
-
Buchstabenhäufigkeit
18+
© Academic, 2000-2024
- Kontaktieren Sie uns: Unterstützung, Werbung
Wörterbücher Export, schritte mit PHP, Joomla, Drupal, WordPress, MODx.