Cantor-Verteilung

Die Cantor-Verteilung ist eine Wahrscheinlichkeitsverteilung, die singulär bezüglich des Lebesgue-Maßes ist. Die dazugehörige Verteilungsfunktion wird als Cantorfunktion oder auch Teufelstreppe bezeichnet.

Plot der Cantorfunktion (10 Iterationen)

Konstruktion der Cantor-Verteilung

Die Cantorverteilung $\mu : \mathcal{B}(\mathbb{R}) \rightarrow [0,1]$ (mit $\mathcal{B}(\mathbb{R})$ als Borelsche σ-Algebra) kann nicht einfach explizit angegeben werden. Sie muss rekursiv konstruiert werden, ähnlich wie die Cantormenge.

1. Variante der Konstruktion

Wenn man vom gleichverteilten Maß auf der Menge {0,1} ausgeht, erhält man auf der Menge $2^{\mathbb N}$ ein Produktmaß. Dieses Maß μ lässt sich so interpretieren: Man betrachtet ein Experiment, in dem unendlich oft eine faire Münze geworfen wird; Elemente von $2^{\mathbb N}$ lassen sich als Ausgänge des Experiments interpretieren (die Folge $(0,1,0,1,\ldots)$ bedeutet zum Beispiel, dass immer abwechselnd Kopf und Zahl aufgetreten sind). Das Maß μ weist einer Teilmenge von $2^{\mathbb N}$ nun seine Wahrscheinlichkeit zu. Zum Beispiel besagt das starke Gesetz der großen Zahlen, dass die Menge G der „gleichverteilten“ Folgen Wahrscheinlichkeit 1 hat, wobei G die folgenden Menge ist:

$G= \left\{(x_0, x_1, \ldots) \left|\ \lim\limits_{n\to \infty}\frac{|\{i<n: x_i=0\}|}{n} = \frac12 \right.\right\}.$

Das oben genannte Maß μ lässt sich durch die oben genannte Bijektion in ein Wahrscheinlichkeitsmaß μ auf der Cantormenge übersetzen. (Eine alternative Beschreibung von μ ergibt sich als Hausdorffmaß zur Dimension ln 2 / ln 3.)

Dieses Wahrscheinlichkeitsmaß μ ist die Cantor-Verteilung, ein Beispiel für ein Maß, dessen Verteilungsfunktion zwar stetig, aber nicht absolut-stetig ist. Die Verteilungsfunktion

$\begin{align} F: [0,1]&\to [0,1]\\ x &\mapsto \mu([0,x] \cap C) \end{align}$

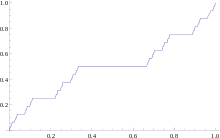
heißt Cantorfunktion (auch „cantorsche Treppenfunktion“). Dabei ist C die Cantormenge, die durch den im zugehörigen Artikel beschriebenen rekursiven „Drittelungs“-Prozess konstruiert werden kann. Auf jedem Intervall im Komplement der Cantormenge ist diese Funktion konstant; auf dem Intervall $\left(\tfrac13, \tfrac23\right)$ hat sie zum Beispiel den Wert 1/2, und auf dem Intervall $\left(\tfrac19, \tfrac29\right)$ hat sie den Wert 1/4.

2. Variante der Konstruktion

Bei dieser Konstruktion wird die Cantorfunktion $F:\mathbb{R} \rightarrow [0,1]$ konstruiert, welche nach dem Korrespondenzsatz die Cantor-Verteilung μ eindeutig bestimmt.

Sei $\mathcal{G}$ das System aller Teilmengen von [0,1], welche als Vereinigung von endlich vielen disjunkten abgeschlossenen nichtleeren Intervallen dargestellt werden kann. Ferner sei $\varphi: \mathcal{G} \rightarrow \mathcal{G}$ gegeben durch (mit $i,m \in \mathbb{N}, a_i,b_i \in [0,1], a_i \leq b_i$)

$\varphi\left(\bigcup_{i \in \{1, \ldots, m\}}[a_i,b_i] \right) := \bigcup_{i \in \{1, \ldots, m\}} \left( \left[a_i, \frac{2a_i+b_i}{3}\right] \cup \left[\frac{a_i+2b_i}{3},b_i\right]\right)$

(Dies entspricht der bereits angesprochen rekursiven Drittelung der Intervalle (Intervall-Länge: b_i-a_i), wobei nur das untere und das obere Drittel mitgenommen werden, während das mittlere Drittel „ausgewischt“ wird .)

Sei weiterhin mit $n \in \mathbb{N}$

$C_n := \varphi^n([0,1])\,.$

Schließlich sei die Cantormenge C definiert durch

$C=\bigcap_{n \in \mathbb{N}}C_n \,.$

Nun wird das Maß $\mu_n: \mathcal{B}(\mathbb{R}) \rightarrow [0,1]$ folgendermaßen definiert:

$\mu_n := \int \left(\frac{3}{2}\right)^n \chi_{C_n}(x)d\lambda(x)$,

wobei λ das eindimensionale Lebesgue-Maß bezeichnet. μ_n ist offensichtlich ein Wahrscheinlichkeitsmaß, die dazugehörige Verteilungsfunktion sei $F_n: \mathbb{R} \rightarrow [0,1]$. Für F_n gilt:

$F_n(x) = \left(\frac{3}{2}\right)^n \lambda(C_n \cap [0,x])$

Für F_n gilt insbesondere F_n(0) = 0 und F_n(1) = 1.

Da F_n | _[0,1] gleichmäßig konvergent ist, ist die Cantorfunktion F durch

$F(x) := \begin{cases} 0 & \text{falls }x \in (-\infty,0]\\ \lim\limits_{n\rightarrow \infty} F_n|_{[0,1]}(x)& \text{falls } x \in (0,1)\\ 1 & \text{falls } x \in [1, \infty) \end{cases}$

eindeutig definiert. Die dazugehörige Verteilung im Sinne der Maßtheorie ist die Cantor-Verteilung.

Eigenschaften

• Die Cantorverteilung ist singulär bezüglich des Lebesgue-Maßes.
• Die Cantorverteilung ist eine symmetrische Verteilung.
• Die Cantorverteilung besitzt keine Lebesgue-Dichte.
• Die Cantorfunktion ist stetig und monoton wachsend zwischen 0 und 1.
• Die Cantorfunktion ist fast überall differenzierbar mit Ableitung 0, aber dennoch nicht konstant.

In der Integrationstheorie ergeben also Ausdrücke der Form

$\int_0^1 g(x) \,{\rm d} F(x)$

einen Sinn, nicht dagegen Ausdrücke der Form

$\int_0^1 g(x) \, \frac{{\rm d} F}{{\rm d}x}(x)\,\mathrm dx.$

Dabei ist g(x) eine beliebige, im Intervall [0,1] Lebesgue-integrierbare Funktion.

Physikalische Realisierungen

Teufelstreppen treten näherungsweise in der Physik in Systemen mit konkurrierenden Längen (z. B. in Adsorbaten oder bei strukturellen Phasenübergängen, die durch das Modell von Frenkel und Kontorowa beschrieben werden) oder mit konkurrierenden Wechselwirkungen (z.B. Magneten oder Legierungen, die durch das ANNNI-Modell beschrieben werden) auf.

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta