Seiteneinteilung

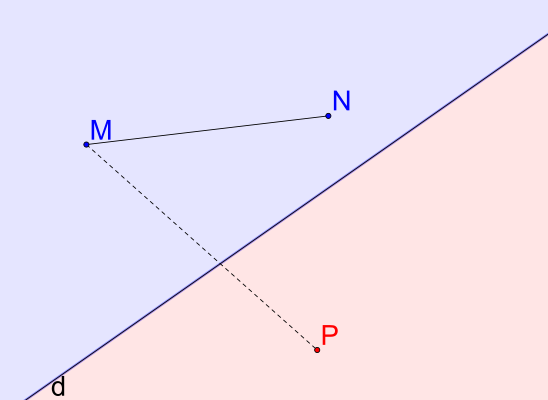
In der elementaren Geometrie der Zeichenebene zerlegt jede Gerade die Ebene in zwei (offene) Halbebenen, die Seiten der Gerade, diese Beobachtung ist zunächst der Anschauung entnommen. Diese Seiteneinteilung lässt sich mathematisch beschreiben als Äquivalenzrelation auf der Menge aller Punkte der Ebene, die nicht auf der einteilenden Gerade liegen.

In der analytischen Geometrie kann dies präzisiert und verallgemeinert werden: In einem n-dimensionalen affinen Raum über einem geordneten Körper liefert jede Hyperebene, also jeder n − 1-dimensionale Teilraum eine Seiteneinteilung des Gesamtraums in zwei Halbräume.

In der synthetischen Geometrie können alle Seiteneinteilungen, die von Geraden einer affinen Ebene bestimmt sind, durch axiomatische Beschreibung einer Seiteneinteilungsfunktion eingeführt werden, mit der die Ebene zu einer schwach angeordneten Ebene wird. Eine solche Seiteneinteilungsfunktion erlaubt es dann, auf dieser Ebene eine schwache Zwischenbeziehung einzuführen, die durch ein zusätzliches Axiom zu einer Zwischenbeziehung im Sinne von Hilberts Axiomensystem der euklidischen Geometrie wird. Ebenen mit einer „starken“ Zwischenbeziehung, die den Hilbertschen Anordnungsaxiomen genügt, heißen angeordnete Ebenen. Schwache Seiteneinteilungsfunktionen existieren für desarguesche affine Ebenen genau dann, wenn der Koordinatenschiefkörper der Ebene einen nichttrivialen quadratischen Charakter zulässt und lassen sich durch einen solchen Charakter eindeutig beschreiben. Jede Anordnung einer desargueschen Ebene entspricht eineindeutig einer Anordnung ihres Koordinatenschiefkörpers.

Dieser Artikel beschreibt hauptsächlich die Seiteneinteilung in einer affinen Ebene im Sinne der synthetischen Geometrie. Dabei wird der Begriff der Seiteneinteilung aus der analytischen Geometrie, der für Ebenen ein Spezialfall des synthetischen Begriffes ist, als Leitidee vorangestellt.

Eine Gerade d und die zwei durch sie bestimmten Halbebenen. M und N liegen auf der gleichen Seite von d, während M und P auf verschiedenen Seiten liegen.

Definitionen

Analytische Geometrie

Für eine übersichtliche Darstellung wird hier ein dreidimensionaler Raum zugrundegelegt. Die Seiteneinteilung kann in gleicher Weise in jedem endlichdimensionalen Raum mit einer Hyperebene anstelle der Ebene vorgenommen werden. Sei K ein geordneter Körper und A der dreidimensionale affine Raum mit dem Koordinatenvektorraum K³. Jede Ebene lässt sich durch eine inhomogene Koordinatengleichung $a_1\cdot x_1+a_2\cdot x_2+a_3\cdot x_3-d=0$ beschreiben. Das Vorzeichen der affinen Funktion $f(x_1,x_2,x_2)=a_1\cdot x_1+a_2\cdot x_2+a_3\cdot x_3-d$ liefert die Seiteneinteilung. Liefert diese Funktion für die Ortsvektoren von zwei Punkten Werte größer 0, dann liegen sie auf derselben Seite der durch f = 0 beschriebenen (Hyper-)Ebene, ebenso, wenn beide Werte kleiner als 0 sind. Ist einer der Werte kleiner und einer größer als 0, dann liegen die Punkte auf verschiedenen Seiten.

Obgleich die Punktkoordinaten und die (Hyper-)Ebenengleichung von dem gewählten Koordinatensystem abhängen, ändert sich die Seiteneinteilung bei einem Wechsel des Koordinatensystems nicht. Sie hängt allein von der Ordnung des geordneten Körpers ab und bestimmt diese sogar eindeutig.

Synthetische Geometrie

Zum 3. Axiom: Zwei verschiedene Geraden (rot), die die Verbindungsgerade PQ (blau) im gleichen Punkt T schneiden, liefern den gleichen Wert der Seiteneinteilungsfunktion für P und Q. Dies ermöglicht es, die Seiteneinteilungsfunktion zu einer (schwachen) Zwischenfunktion zu machen.

Sei A eine affine Inzidenzebene, G die Menge ihrer Geraden und $\mathbf R$ die Menge der Tripel

$\mathbf R= \lbrace (g,P,Q)\in G\times A\times A |P\not\in g \and Q\not\in g\rbrace;$

dann heißt eine Abbildung $S: \mathbf R\rightarrow C_2$ in die zyklische Gruppe $(C_2,\cdot)=\left(\lbrace -1,1\rbrace,\cdot\right)$ eine (schwache) Seiteneinteilungsfunktion, wenn folgende Axiome erfüllt sind:

1. S(g,P,Q) = S(g,Q,P).
2. $S(g,P,Q)\cdot S(g,Q,R) \cdot S(g,R,P)=+1.$
3. Sind $P\neq Q, PQ\neq g, PQ\neq h$ und PQ,g,h kopunktal, dann ist S(g,P,Q) = S(h,P,Q).
4. Sind $P\neq Q, PQ\parallel g$ und $PQ\neq g$, so ist S(g,P,Q) = + 1.
5. Für jede Gerade g existieren Punkte mit $P,Q\not\in g$ und S(g,P,Q) = − 1.

Eine affine Inzidenzebene mit einer Seiteneinteilungsfunktion heißt schwach angeordnet.

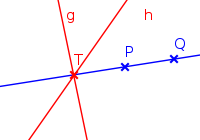
Aus den ersten beiden Axiomen folgt, dass die Eigenschaft S(g,P,Q) = + 1 („auf der gleichen Seite liegen“) bei fester Gerade g eine Äquivalenzrelation für Punkte ist, die nicht auf der Geraden liegen. Das 4. Axiom besagt, dass Parallelen einer Geraden ganz auf einer Seite der Geraden liegen, das 5. Axiom fordert, dass es zu jeder Geraden zwei verschiedene Seiten gibt. Das 3. Axiom, das auch als Geradenrelation bezeichnet wird, fordert, dass die Seiteneinteilung, die eine schneidende Gerade g auf einer bestimmten Geraden PQ einführt, nur von dem Schnittpunkt $T\in g\cap PQ$ abhängt.

Zusammenhang zwischen den Definitionen

Definiert man für eine affine Ebene über einem geordneten Körper die Seiteneinteilungsfunktion durch

$S(g,P,Q)= \sgn (a_1\cdot p_1+a_2\cdot p_2-d) \cdot \sgn(a_1\cdot q_1+a_2\cdot q_2-d),$

wobei sgn  die Vorzeichenfunktion ist, $a_1\cdot x_1+a_2\cdot x_2-d=0$ eine Gleichung der Gerade g und P(p₁ | p₂) Q(q₁ | q₂) die Koordinaten der Punkte sind, dann wird diese affine Ebene damit zu einer schwach angeordneten (sogar einer angeordneten) Ebene im Sinne der synthetischen Geometrie und alle abgeleiteten Begriffe sind anwendbar. Insbesondere sind die Seiteneinteilungen, die zwei unterschiedliche Geraden erzeugen, miteinander verträglich im Sinne des 3. Axioms – für schneidende Geraden – bzw. des 4. Axioms – für parallele Geraden.

Eigenschaften und abgeleitete Begriffe

• Für jede Gerade g existieren zwei disjunkte, nichtleere Mengen, die Seiten von g, wobei zwei Punkte $P,Q\in A\setminus g$ genau dann zur gleichen Seite gehören, wenn S(g,P,Q) = + 1 ist.
• Die Seite von g, die einen bestimmten Punkt $P\in A\setminus g$ enthält, wird als gP ⁺ , die andere Seite als gP ⁻ notiert.
• Es gilt $A=gP^+\dot \cup g \dot \cup gP^-.$
• Die Vereinigung $X=gP^+\cup g$ wird als (abgeschlossene) Halbebene bezeichnet, die Seite als deren Inneres $X^\circ=gP^+$, die Gerade als deren Rand $\partial X=g$.
• Die Halbebenen $gP^+\cup g$ und $gP^-\cup g$ heißen zueinander entgegengesetzt.
• Der Schnitt zweier entgegengesetzter Halbebenen ist ihr gemeinsamer Rand.
• Eine Gerade, die zum Rand einer Halbebene parallel ist und mit der Halbebene mindestens einen Punkt gemeinsam hat, liegt ganz in der Halbebene.
• Eine Gerade ist genau dann nicht parallel zum Rand einer Halbebene, wenn sie Punkte der Halbebene enthält, aber nicht ganz in der Halbebene liegt.
• Der Durchschnitt einer Halbebene X mit einer Geraden h, die nicht parallel zum Rand $\partial X$ ist, wird als Halbgerade bezeichnet, $T\in\partial X \cap h$ als ihr Anfangspunkt, h als Trägergerade der Halbgeraden. Zwei Halbgeraden, die als Durchschnitte von h mit zwei entgegengesetzten Halbebenen entstehen, heißen entgegengesetzt.
• Aufgrund des 3. Axioms der Seiteneinteilungsfunktion gibt es zu einer Geraden g und einem Anfangspunkt $T\in g$ genau zwei Halbgeraden und diese hängen als Mengen nicht davon ab, welche Gerade h ($h\neq g$) durch T die definierenden entgegengesetzten Halbebenen ausschneidet.

Die hier definierten Begriffe lehnen sich an topologische Begriffe („Inneres“, „Rand“) an. Legt man die Menge aller Seiten (das „Innere“ für alle Halbebenen) als Subbasis zugrunde, dann wird dadurch auf der Ebene tatsächlich eine Topologie definiert. Enthält die Ebene unendlich viele Punkte, was für eine affine Ebene über einem geordneten Körper stets der Fall ist, dann gelten die definierten Begriffe auch im topologischen Sinn. In einer endlichen Ebene entsteht allerdings eine triviale, nämlich die diskrete Topologie.

Zwischenrelation

Zu jeder Seiteneinteilungsfunktion S auf einer affinen Ebene gibt es eine eindeutig bestimmte Abbildung $\overline S$ auf der Menge der kollinearen Punktetripel der Ebene

$\overline{\mathbf R}=\lbrace(T,P,Q)\in A\times A \times A| T,P,Q \quad\text{sind kollinear},T\neq P, T\neq Q\rbrace.$

Sie wird definiert, indem für irgendeine Gerade g durch T, die weder durch P noch durch Q geht,

$\overline S(T,P,Q)=S(g,P,Q)$

gesetzt wird. Dass diese Definition unabhängig von der Wahl von g ist, folgt aus dem 3. Axiom für die Seiteneinteilungsfunktion. Die surjektive Funktion $\overline S:\, \overline{\mathbf R} \rightarrow C_2$ heißt die von der Seiteinteilungsfunktion induzierte schwache Zwischenfunktion. Die schwache Zwischenfunktion ist invariant unter Parallelprojektionen.

Zum Axiom (Z) einer schwachen Zwischenfunktion: In einem nichtentarteten Dreieck (rote Punkte) bilden 3 Punkte (blau), die zwischen unterschiedlichen Punktepaaren des Ausgangsdreiecks liegen, wieder ein nichtentartetes Dreieck.

Man sagt dann, „T liegt zwischen P und Q“, wenn $(T,P,Q)\in\overline{\mathbf R }$ und $\overline{S}(T,P,Q)=-1$ ist und nennt diese dreistellige Relation schwache Zwischenbeziehung. Diese Relation erfüllt folgende Axiome (→ vergleiche dazu Gruppe II, Axiome der Anordnung in Hilberts Axiomensystem):

(A1) Liegt T zwischen P und Q, dann sind die drei Punkte kollinear und T liegt auch zwischen Q und P.

(A2) Sind P und Q verschiedene Punkte, so existiert ein Punkt T, der zwischen ihnen liegt.

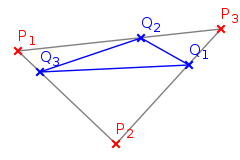
(A4, Axiom von Pasch) Sind P₁,P₂,P₃ drei nicht kollineare Punkte, und ist g eine Gerade, die durch keinen dieser Punkte geht und einen Punkt zwischen P₁ und P₂ enthält, dann enthält g auch einen Punkt zwischen P₂ und P₃ oder einen zwischen P₃ und P₁.

(Z) Sind P₁,P₂,P₃ drei nicht kollineare Punkte und Q₁,Q₂,Q₃ Zwischenpunkte der drei Verbindungsstrecken dieses Dreiecks, dann sind auch Q₁,Q₂,Q₃ nicht kollinear.

Das Axiom (Z) lässt sich auch gleichwertig als Ergänzung zu (A4), dem Axiom von Pasch formulieren: „…dann enthält g auch einen Punkt zwischen P₂ und P₃ oder einen zwischen P₃ und P₁, niemals beides!“ – Das „Oder“ in dem Axiom (A4) wird also durch (Z) zum ausschließenden Oder.

Nun gilt: Genügt eine dreistellige Relation in einer affinen Inzidenzebene den Axiomen (A1), (A2), (A4) und (Z), dann existiert eine eindeutig bestimmte Seiteneinteilungsfunktion S, aus der sich diese Zwischenbeziehung über die von S induzierte Zwischenfunktion wie oben beschrieben definieren lässt. Die Seiteneinteilungsfunktion kann aus der Zwischenfunktion direkt berechnet werden:

$S(g,P,Q)=\begin{cases} +1,\;\text{ falls}\; P=Q \text{ oder } PQ\parallel g\\ \overline{S}(T,P,Q)\; \text{ mit } T\in g\cap PQ,\;\text{falls } P\neq Q\, \text{ und } PQ\not\parallel g. \end{cases}$

Schwache Anordnung auf desargueschen Ebenen

Eine desarguesche Ebene ist isomorph zu einer Koordinatenebene über einem Schiefkörper K. Zu drei kollinearen Punkten T,P,Q mit $T\neq P$ gibt es immer ein Element $\alpha\in K$, den Streckungsfaktor $\alpha=\operatorname{SF}(T,P,Q)$ mit $\alpha(\overrightarrow{TP})=\overrightarrow{TQ}$, umgekehrt gibt es zu jedem $\alpha\in K$ ein kollineares Punktetripel mit $\alpha=\operatorname{SF}(T,P,Q)$ (→ siehe dazu Affine Translationsebene). Weil sowohl der Streckungsfaktor als auch die Zwischenfunktion invariant unter Parallelprojektionen ist, kann man eine wohldefinierte Zuordnung

$K^*\rightarrow C_2,\quad \alpha \mapsto \overline{S}(T,P,Q);\quad \alpha=\operatorname{SF}(T,P,Q)$

definieren, die ein nichttrivialer quadratischer Charakter von K ist.

Umgekehrt kann jeder nichttriviale quadratische Charakter χ des Schiefkörpers zur Definition einer schwachen Zwischenfunktion verwendet werden:

$\overline{S}:\overline{\mathbf R}\rightarrow C_2,\quad (T,P,Q)\mapsto \chi\left(\operatorname{SF}(T,P,Q)\right).$

Jede schwache Seiteneinteilung auf einer desargueschen Ebene wird so durch einen nichttrivialen quadratischen Charakter des Koordinatenschiefkörpers induziert und umgekehrt. Auf einer desargueschen Ebene existiert also genau dann eine schwache Seiteneinteilungsfunktion, wenn sein Koordinatenschiefkörper einen nichttrivialen quadratischen Charakter zulässt und zu jedem solchen Charakter existiert eine schwache Anordnung der Ebene.

Angeordnete Ebene

Das dritte Hilbertsche Anordnungsaxiom lautet

(A3) Liegt T zwischen P und Q, so liegt Q nicht zwischen P und T.

Aus den Hilbertschen Axiomen (A1) bis (A4) folgt das Axiom (Z). Eine affine Ebene mit einer Zwischenrelation, die die Axiome (A1) bis (A4) und damit automatisch auch (Z) erfüllt, wird als angeordnete Ebene bezeichnet.

Eigenschaften

• In einer angeordneten affinen Inzidenzebene liegt von drei verschiedenen kollinearen Punkten genau einer zwischen den beiden anderen.
• Jede angeordnete affine Inzidenzebene ist auch schwach angeordnet.
• Die Anordnung (Zwischenbeziehung) lässt sich mit einer eindeutig durch sie bestimmten Seiteneinteilungsfunktion bzw. mit der durch sie bestimmten Zwischenfunktion beschreiben. Sie ist also im Falle einer desargueschen Ebene wie die schwache Anordnung durch einen nichttrivialen quadratischen Charakter eindeutig bestimmt.
• In einer angeordneten Ebene und in einer endlichen, schwach angeordneten Ebene gilt das affine Fano-Axiom, daher existiert in diesen Fällen zu zwei beliebigen Punkten stets ein Mittelpunkt. Dieser Mittelpunkt liegt dann immer (im Sinne der jeweiligen Zwischenbeziehung) zwischen den beiden Punkten.
• Kann die affine Translationsebene, die durch Schlitzen aus einer Moufangebene entsteht, zu einer angeordneten Ebene gemacht werden, dann sind beide Ebenen desarguesch.^[1]

Desarguesche angeordnete Ebene

Die Anordnung eines Schiefkörpers K muss die gleichen Axiome erfüllen wie die Ordnung eines geordneten Körpers, woraus folgt, dass sie durch einen Positivbereich $K^+=\!\,\lbrace \alpha \in K | 0<\alpha \rbrace$ eindeutig bestimmt ist, der folgende Eigenschaften hat (→ vergleiche geordneter Körper):

1. $a,b\in K^+ \Rightarrow a+b\in K^+,$
2. $a,b\in K^+ \Rightarrow a\cdot b\in K^+,$
3. für jedes $a\in K$ gilt genau eine der Beziehungen $a\in K^+,\, -a\in K^+, a=0$.

Durch jeden solchen Positivbereich ist ein quadratischer Charakter χ bestimmt, der auf K ⁺ positiv, auf − K ⁺ negativ ist und χ( − 1) = − 1 erfüllt. Umgekehrt bestimmt jeder quadratische Charakter mit χ( − 1) = − 1 einen Bereich L = χ ^{− 1}(1), der allerdings im allgemeinen nur die 2. und 3. Eigenschaft eines Positivbereiches hat.

Der folgende Satz klärt den Zusammenhang zwischen der Anordnung einer desargueschen Ebene und der Anordnung ihres Koordinatenschiefkörpers:

Der Koordinatenschiefkörper einer angeordneten desargueschen Ebene lässt eine Anordnung zu. Umgekehrt lässt die affine Ebene über einem angeordneten Schiefkörper sich anordnen. Jede Anordnung des Schiefkörpers induziert eine „starke“ Zwischenfunktion auf der Ebene und umgekehrt. Der Zusammenhang wird durch die Gleichwertigkeit

$\overline S(T,P,Q)=+1 \Leftrightarrow \operatorname{SF} (T,P,Q)>0$

für alle $(T,P,Q)\in\overline{R}$ vermittelt.

Beispiele

• Die affine Ebene über einem geordneten Körper wird durch die oben beschriebene Seiteneinteilungsfunktion zu einer angeordneten Ebene. Der quadratische Charakter ordnet jeder Zahl des Körpers außer 0 ihr Vorzeichen als Zahl in C₂ = { − 1, + 1} zu.
• Ein formal reeller Körper lässt mindestens eine Ordnung zu, die ihn zu einem geordneten Körper macht. Jede dieser Körperordnungen bestimmt wie im vorigen Beispiel einen nichttrivialen quadratischen Charakter und damit eine Anordnung der affinen Ebene über dem Körper.
• Ein euklidischer Körper lässt nur einen nichttrivialen quadratischen Charakter zu, der jeder Quadratzahl 1 und jeder Nichtquadratzahl −1 zuordnet, (siehe dazu auch Quadratklasse). Daher ist auf der affinen Ebene über einem solchen Körper genau eine schwache Seiteneinteilung möglich, mit der diese Ebene zu einer „stark“ angeordneten Ebene wird.

• Zu den euklidischen Körpern zählen die reellen Zahlen und allgemeiner jeder reell abgeschlossene Körper.

• Der Körper der komplexen Zahlen und allgemeiner jeder algebraisch abgeschlossene Körper lässt nur den trivialen Charakter als quadratischen Charakter zu. Daher ist auf einer affinen Ebene über einem solchen Körper keine schwache Anordnung möglich.
• Auf dem Körper der rationalen Zahlen können unendlich viele nichttriviale quadratische Charaktere definiert werden: Teilt man die Menge der Primzahlen willkürlich in zwei disjunkte Teilmengen P ₊ und P ₋ auf, dann wird durch χ(P ₊ ) = + 1,χ(P ₋ ) = − 1 und die Wahl eines Vorzeichens für χ( − 1) ein Charakter χ eindeutig bestimmt. Damit sind alle quadratischen Charaktere von $\Q^*$ beschrieben. Jeder dieser Charaktere außer dem trivialen ($P_-=\emptyset,\chi(-1)=1$) bestimmt eine schwache Anordnung der affinen Ebene über $\Q$. Genau für den durch $P_-=\emptyset, \chi(-1)=-1$ beschriebenen Charakter ist die schwache Anordnung eine Anordnung, die „gewöhnliche“ Anordnung der rationalen Ebene.
• Jeder Restklassenkörper $K=\Z /p\Z$ zu einer ungeraden Primzahl p besitzt ein Element β, das die zyklische multiplikative Gruppe K ^* des Körpers erzeugt. Durch χ(β) = − 1 ist ein nichttrivialer quadratischer Charakter auf K ^* als Gruppenhomomorphismus eindeutig definiert. Dies ist der einzige nichttriviale quadratische Charakter des Körpers, daher kann die desarguesche Ebene über einem solchen Körper auf genau eine Art schwach angeordnet werden.

• Dies gilt allgemeiner und aus den gleichen Gründen für jeden endlichen Körper mit ungerader Charakteristik.

• Die affine Ebene über dem Restklassenkörper $K=\Z /13\Z$ wird durch ihren einzigen nichttrivialen quadratischen Charakter zu einer schwach angeordneten Ebene. 2 ist ein erzeugendes Element von K ^* . Für ein Punktetripel (T,P,Q) mit $\operatorname{SF}(T,P,Q)=2^2=4$ ändert sich die Zwischenfunktion bei zyklischer Vertauschung der Punkte in dem Tripel nicht. Daher liegt keiner der drei verschiedenen kollinearen Punkte zwischen den beiden anderen.^[2]
• Ist F ein beliebiger Körper und K = F(X) der rationale Funktionenkörper über diesem Körper, dann kann durch den Grad der rationalen Funktion $\frac{f}{g} \neq 0$ ein nichttrivialer quadratischer Charakter auf K eingeführt werden: $\chi \left( \frac{f}{g} \right)=-1$ genau dann, wenn $\deg \left(\frac{f}{g}\right)=\deg (f)-\deg(g)$ ungerade ist. Durch diesen Charakter lässt sich die affine Ebene über K schwach anordnen. – Dies ist also auch über gewissen unendlichen Körpern mit Charakteristik 2 möglich!
• Ein endlicher Körper mit Charakteristik 2 lässt keinen nichttrivialen quadratischen Charakter zu, daher existiert auf einer affinen Ebene über einem solchen Körper nie eine Seiteneinteilung.

Literatur

• Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie, Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
• Erich Glock: Die Orientierungsfunktionen eines affinen Raumes, aus: Mathematische Zeitschrift. Bd 78. 1962 S. 319-360
• Erich Glock: Ordnungsfunktionen, die auf Seiteneinteilungen besonderer Art führen. in: Mathematics and Statistics, Archiv der Mathematik Volume 12, Number 1, 71-77, PDF Volltext
• Günter Pickert: Projektive Ebenen. 2. Auflage, Berlin-Heidelberg-New York 1975
• Emanuel Sperner: Die Ordnungsfunktionen einer Geometrie, Math. Ann. 121 (1949) 107-130
• Emanuel Sperner: Beziehungen zwischen geometrischer und algebraischer Anordnung, Sitzungsbericht Heidelberger Akad. Wiss. Math. Naturwiss. Klasse 1949, 413-448

Einzelnachweise

1. ↑ Pickert (1975) S. 240
2. ↑ Degen (1976) S. 105