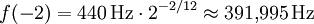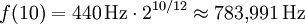12-EDO

Bei der gleichstufigen (auch gleichtemperierten oder gleichschwebenden) Stimmung gleicht man das Pythagoreische Komma aus und teilt die Oktave in zwölf Halbton-Schritte mit dem Frequenzverhältnis

$\frac{f_2}{f_1} = \sqrt[12] \tfrac 2 1 \approx 1{,}05946309$

Zusammenhang von Frequenz, Halbton und Oktave

Ein derart gestimmtes Instrument enthält außer der Oktave kein einziges „ideales“, d. h. in einem einfach ganzzahligen Frequenzverhältnis rein gestimmtes Intervall mehr, und die Abweichungen sind auch durchaus hörbar. In der heutigen Musikwahrnehmung wird dieses jedoch allgemein als akzeptabel empfunden (Gewöhnungseffekt).

Andersherum interpretiert ist es eine kuriose Besonderheit der Mathematik, dass die Tonhöhen der gleichstufigen und der reinen Stimmung doch so nahe beieinander liegen, dass sie in der Praxis vermengt werden können, ohne dass es dem Laienohr auffällt. Die ganze Harmonik der Musik wäre sonst gar nicht möglich.

Die Einteilung der Oktave in zwölf Töne mit gleichem Frequenzverhältnis zu ihren Nachbartönen ist zwar die gebräuchlichste, aber nicht die einzige Möglichkeit, um sich reinen Intervallen anzunähern. Mit mehr Tönen pro Oktave lassen sich bessere Näherungen erreichen. Eine Einteilung, die tatsächlich Verwendung gefunden hat, ist ein gleichstufig gestimmtes neunzehnstufiges Tonsystem.

Geschichte

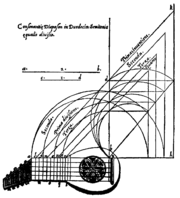Geometrische Darstellung der gleichstufigen Stimmung aus Sopplimenti musicali (1588) von Gioseffo Zarlino

Die gleichstufige Stimmung konnte erstmals 1584 von Chu Tsai-yü ( 朱載堉 ) in China mit Hilfe eines Systems neunstelliger Zahlen ziemlich genau berechnet werden. In Europa wurden diese Berechnungen allerdings erst 1799 bekannt, ohne dass Chu Tsai-yü namentlich genannt wurde. 1588 bot Gioseffo Zarlino eine exakte geometrische Darstellung. Simon Stevin beschrieb als erster Europäer in Vande Spiegheling der Singconst (Manuskript um oder vor 1600) eine weitgehende Annäherung mit Hilfe eines von ihm entwickelten Verfahrens zur Wurzelberechnung, meinte allerdings fälschlicherweise, dabei natürliche große Terzen zu gewährleisten.

Als gleichstufig bezeichnete Lautenstimmungen des 16. Jahrhunderts fußten, wie von Vincenzo Galilei praktiziert, meist auf dem Halbton mit dem Verhältnis 18:17 (etwa 99 Cent).

Vor allem im 17. Jahrhundert wurde die gleichstufige Stimmung nicht nur von Theoretikern wie z. B. Pietro Mengoli und Marin Mersenne, sondern auch von Komponisten, Instrumentenbauern und ausübenden Musikern diskutiert. Das belegt beispielsweise eine Auseinandersetzung über Stimmungen zwischen Giovanni Artusi und Claudio Monteverdi kurz nach 1600. Girolamo Frescobaldi empfahl die gleichstufige Stimmung für die Orgel in der Basilica S. Lorenzo in Damaso.

Im deutschen Sprachraum verwendete man für gleichstufig den Begriff gleichschwebend, so Andreas Werckmeister 1707 in Musikalische Paradoxal-Discourse: „ ... wenn die Temperatur also eingerichtet wird/daß alle Quinten 1/12 Commat: ... schweben, und ein accurates Ohr dieselbe auch zum Stande zu bringen und zu stimmen weiß/so dann gewiß eine wohltemperirte Harmonia, durch den gantzen Circul und durch alle Clavis sich finden wird.“ Werckmeister meint damit ausdrücklich nicht, dass die Schwebungsfrequenzen gleich seien. Die von ihm angesprochene Schwierigkeit, gleichstufig zu stimmen, kann z. B. ein Klavierstimmer gerade dadurch meistern, dass er die unterschiedlichen Schwebungsfrequenzen der Quinten in den verschieden hohen Lagen des Klavieres kennt und zum Stimmen nutzt.

Der Begriff gleichschwebend kann aber auch auf eine weitere Besonderheit dieser Stimmung bezogen werden: Die Oberquinte eines Tones und die Unterquinte seiner Oktave schweben stets gleich schnell.

Die praktische Bedeutung blieb indes bis ins 18. Jahrhundert gering. Es mehrten sich aber die Befürworter der gleichstufigen Stimmung, zu denen z. B. Jean-Philippe Rameau und Friedrich Wilhelm Marpurg gehörten. Bis gegen Ende des 18. Jahrhunderts gewann die gleichstufige Stimmung die Oberhand gegenüber ungleichstufigen Stimmungen und setzte sich im 19. Jahrhundert endgültig durch.

Damit verloren allerdings die Tonarten-Charaktere für neue Kompositionen an Bedeutung, weil verschiedene Tonarten in dieser Hinsicht nicht mehr unterschiedlich klangen. Beim Aufführen älterer Werke auf gleichstufig gestimmten Instrumenten gehen aus demselben Grund häufig wesentliche künstlerische Aspekte der Komposition verloren, so setzten beispielsweise ältere Komponisten zu ihrer Zeit gerne schlecht klingende „unmögliche“ Tonarten ein, um negative Sachverhalte wie Schmerz oder Sünde klanglich erlebbar zu machen.

Heute werden Instrumente mit festen Tonhöhen, wie das Klavier oder die Gitarre, standardmäßig gleichstufig gestimmt. Viele Orgeln und Cembali aber werden historisierend mit anderen, ungleichstufigen Stimmungen versehen.

Frequenzberechnung

Die mathematische Vorschrift zur Bestimmung der Töne auf der gesamten Tonleiter der gleichstufigen Stimmung lautet

$f(i) = f_0 \cdot 2^{i/12} \,$,

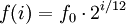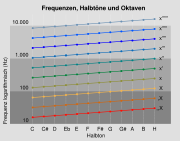
wobei f₀ z. B. die Frequenz des Kammertons a’ (440 Hz) sein kann. i ist die Halbtonschritt-Entfernung zu dem gewählten Ton mit der Frequenz f₀. Eine solche mathematische Folge nennt man geometrische Folge. Man erhält bei einer linearen Auftragung der Frequenz über den Tonnamen eine halblogaritmische Skala, hier allerdings nicht mit dem Zehner- sondern dem Zweierlogarithmus.

Möchte man beispielsweise die Frequenz des Tones g’ bestimmen, so zählt man seine Halbtonschritt-Entfernung vom Kammerton a’ ab (i = minus 2, da man nach unten zählt), und setzt die Werte in die Gleichung ein:

$f(-2) = 440\,\mathrm{Hz} \cdot 2^{-2/12} \approx 391{,}995\,\mathrm{Hz} \,$

für den Ton g’’ erhält man entsprechend einen Halbtonabstand zu f₀ von i = 10:

$f(10) = 440\,\mathrm{Hz} \cdot 2^{10/12} \approx 783{,}991\,\mathrm{Hz} \,$

Wie man sieht, besitzt g’’ die doppelte Frequenz wie g’ – daher klingt es so konsonant, wenn man zwei gleichnamige Töne anspielt, womit auch eine Haupteigenschaft der gleichstufigen Stimmung erklärt ist. Ein anderer Vorteil liegt darin, dass man jedes Stück transponieren kann (also z. B. alle Töne von dem ursprünglichen Fis-Dur nach C-Dur verschieben), ohne dass sich für einen gewöhnlichen Zuhörer an dem Stück etwas charakteristisch verändert (Menschen mit absolutem Gehör ausgenommen).

Centwerte der gleichstufigen Stimmung

Ton	C	Cis/Des	D	Dis/Es	E	F	Fis/Ges	G	Gis/As	A	Ais/B	H	C
Centwert	0	100	200	300	400	500	600	700	800	900	1000	1100	1200

Die folgende Tabelle zeigt die Werte aller Intervalle, in gleichstufiger und reiner Stimmung sowie deren Abweichung voneinander in Cent:

Intervall	Gleichstufig temperiertes Intervall	Reines Intervall	Differenz in Cent
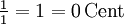
Prime	$\sqrt[12]{2^0} = 1 = 0\,\mathrm{Cent}$	$\tfrac{1}{1} = 1 = 0\,\mathrm{Cent}$	0 Cent
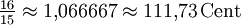
Kleine Sekunde	$\sqrt[12]{2^1} = \sqrt[12]{2} \approx 1{,}059463 = 100\,\mathrm{Cent}$	$\tfrac{16}{15} \approx 1{,}066667 \approx 111{,}73\,\mathrm{Cent}$	-11,73 Cent
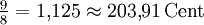
Große Sekunde	$\sqrt[12]{2^2} = \sqrt[6]{2} \approx 1{,}122462 = 200\,\mathrm{Cent}$	$\tfrac{9}{8} = 1{,}125 \approx 203{,}91\,\mathrm{Cent}$	-3,91 Cent
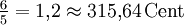
Kleine Terz	$\sqrt[12]{2^3} = \sqrt[4]{2} \approx 1{,}189207 = 300\,\mathrm{Cent}$	$\tfrac{6}{5} = 1{,}2 \approx 315{,}64\,\mathrm{Cent}$	-15,64 Cent
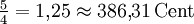
Große Terz	$\sqrt[12]{2^4} = \sqrt[3]{2} \approx 1{,}259921 = 400\,\mathrm{Cent}$	$\tfrac{5}{4} = 1{,}25 \approx 386{,}31\,\mathrm{Cent}$	13,69 Cent
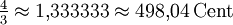
Quarte	$\sqrt[12]{2^5} = \sqrt[12]{32} \approx 1{,}334840 = 500\,\mathrm{Cent}$	$\tfrac{4}{3} \approx 1{,}333333 \approx 498{,}04\,\mathrm{Cent}$	1,96 Cent
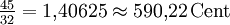
Übermäßige Quarte *	$\sqrt[12]{2^6} = \sqrt{2} \approx 1{,}414214 = 600\,\mathrm{Cent}$	$\tfrac{45}{32} = 1{,}40625 \approx 590{,}22\,\mathrm{Cent}$	9,78 Cent
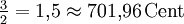
Quinte	$\sqrt[12]{2^7} = \sqrt[12]{128} \approx 1{,}498307 = 700\,\mathrm{Cent}$	$\tfrac{3}{2} = 1{,}5 \approx 701{,}96\,\mathrm{Cent}$	-1,96 Cent
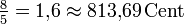
Kleine Sexte	$\sqrt[12]{2^8} = \sqrt[3]{4} \approx 1{,}587401 = 800\,\mathrm{Cent}$	$\tfrac{8}{5} = 1{,}6 \approx 813{,}69\,\mathrm{Cent}$	-13,69 Cent
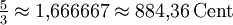
Große Sexte	$\sqrt[12]{2^9} = \sqrt[4]{8} \approx 1{,}681793 = 900\,\mathrm{Cent}$	$\tfrac{5}{3} \approx 1{,}666667 \approx 884{,}36\,\mathrm{Cent}$	15,64 Cent
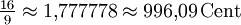
Kleine Septime	$\sqrt[12]{2^{10}} = \sqrt[6]{32} \approx 1{,}781797 = 1000\,\mathrm{Cent}$	$\tfrac{16}{9} \approx 1{,}777778 \approx 996{,}09\,\mathrm{Cent}$	3,91 Cent
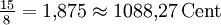
Große Septime	$\sqrt[12]{2^{11}} = \sqrt[12]{2048} \approx 1{,}887749 = 1100\,\mathrm{Cent}$	$\tfrac{15}{8} = 1{,}875 \approx 1088{,}27\,\mathrm{Cent}$	11,73 Cent
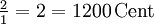
Oktave	$\sqrt[12]{2^{12}} = 2 = 1200\,\mathrm{Cent}$	$\tfrac{2}{1} = 2 = 1200\,\mathrm{Cent}$	0 Cent
Anmerkungen: * Übermäßige Quarte, mitunter auch als Tritonus bezeichnet, definiert als: Große Terz (5/4) plus Große Sekunde (9/8). Das ist gleichbedeutend mit: Quinte (3/2) minus diatonischer Halbton (16/15). Ist die Differenz negativ, so ist das gleichtemperierte Intervall enger als das reine.

Siehe auch

• Frequenzen der gleichstufigen Stimmung
• Quintenzirkel
• Cent

Literatur

• Mark Lindley: Stimmung und Temperatur, in Frieder Zaminer (Hrsg.): Geschichte der Musiktheorie, Bd. 6. Hören Messen und Rechnen in der frühen Neuzeit, S. 109-332, Darmstadt 1987

Stimmungen des abendländischen zwölfstufigen Tonsystems
Aulos-Modi | Pythagoreische Stimmung | Reine Stimmung | Mitteltönige Stimmung | Wohltemperierte Stimmung | Werckmeister-Stimmung | Silbermann-Sorge-Temperatur | Kirnberger-Stimmung | Gleichstufige Stimmung | Vallotti-Stimmung

Weblinks

• Intervall-Umrechnung - Frequenzverhältnis nach cent und cent nach Frequenz