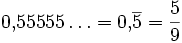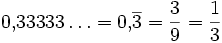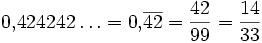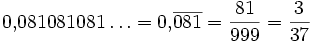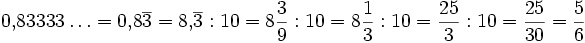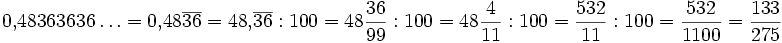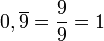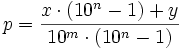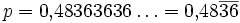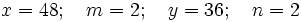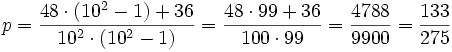Denär

Das Dezimalsystem (von Lateinisch: Dezimus = „der Zehnte“), auch als Zehnersystem oder Denärsystem bezeichnet, ist ein Stellenwertsystem zur Darstellung von Zahlen. Es verwendet die Grundzahl (oder Basis) 10. Das Dezimalsystem ist heute das weltweit verbreitetste Zahlensystem und stammt ursprünglich aus Indien.

Vermutlich hat das Dezimalsystem seinen Ursprung im Umstand, dass der Mensch zehn Finger hat, die den weniger geübten als Rechenhilfe dienen konnten. Mathematisch gesehen wäre das Duodezimalsystem zur Basis 12 praktischer, da die Zahl 12 durch die Zahlen 2, 3, 4 und 6 teilbar ist. Die Sumerer und Babylonier, bei denen sich das Stellenwertsystem zum ersten Mal nachweisen lässt, haben sogar ein 60er-System benutzt, das zusätzlich auch noch die restfreie Teilung durch 5 ermöglicht. Nicht zufällig ist noch heute das Dutzend eine Handelseinheit oder wird der Tag in 2 mal 12 Stunden à 60 Minuten à 60 Sekunden eingeteilt.

Definition und Darstellung

Ziffern

Im Dezimalsystem verwendet man die zehn Ziffern

0 (Null), 1 (Eins), 2 (Zwei), 3 (Drei), 4 (Vier), 5 (Fünf), 6 (Sechs), 7 (Sieben), 8 (Acht), 9 (Neun).

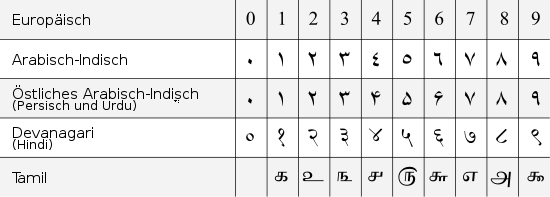
Diese Ziffern werden jedoch in verschiedenen Teilen der Welt unterschiedlich geschrieben. Siehe dazu die Artikel Arabische und Indische Ziffern.

Indische Zifferzeichen werden auch heute noch in den verschiedenen indischen Schriften (Devanagari, Bengalische Schrift, Tamilische Schrift usw.) verwendet. Sie unterscheiden sich stark voneinander.

Definition

Eine Dezimalzahl wird in der Form

$\pm z_m z_{m-1} \ldots z_0\operatorname{,}z_{-1} z_{-2} \ldots z_{-n} \qquad \left(m,n\in\mathbb{N} \quad z_i\in\{0,\ldots,9\}\right)$

aufgeschrieben. Dabei ist jedes z_i eine der oben genannten Ziffern. Der Index i beschreibt den Stellenwert der jeweiligen Ziffer, die Wertigkeit einer Ziffer ist die Zehnerpotenz 10ⁱ. Die Ziffern werden ohne Trennzeichen hintereinander geschrieben, wobei bei rechtsläufigen Schriften die höchstwertige Stelle mit der Ziffer z_m ganz links und die niederwertigeren Stellen mit den Ziffern z_m-1 bis z₀ in absteigender Reihenfolge rechts davon stehen. Zur Darstellung von rationalen Zahlen mit nicht-periodischer Entwicklung folgen dann, nach einem trennenden Komma, die Ziffern z _-1 bis z _-n. Im englischen Sprachraum wird statt des Kommas meist ein Punkt verwendet.

Ziffern vor dem Komma werden mit einer Zehnerpotenz mit einem positiven Exponenten multipliziert (Ausnahme: zur ersten Stelle links vom Komma gehört der Exponent Null), die Ziffern nach dem Komma dagegen mit einer Zehnerpotenz mit einem negativen Exponenten. Der Wert Z der Dezimalzahl ergibt sich also durch Summierung dieser Ziffern, welche vorher jeweils mit ihrem Stellenwert 10ⁱ multipliziert werden; zusätzlich ist (zumindest bei negativen Zahlen) das Vorzeichen voranzustellen:

$Z = \pm \sum_{i=-n}^m z_i \cdot 10^i$.

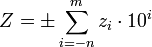Diese Darstellung nennt man auch Dezimalbruch-Entwicklung.

Beispiel

723,48 = 7·10² + 2·10¹ + 3·10⁰ + 4·10^-1 + 8·10^-2

Dezimalbruchentwicklung

Mit Hilfe der Dezimalbruchentwicklung kann man jeder reellen Zahl eine Folge von Ziffern zuordnen. Jeder endliche Teil dieser Folge definiert einen Dezimalbruch, der eine Näherung der reellen Zahl ist. Man erhält die reelle Zahl selbst, wenn man von den endlichen Summen der Teile zur unendlichen Reihe über alle Ziffern übergeht. Diese Darstellung ist ein Beispiel einer Reihenentwicklung.

Formal wird mit 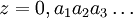$z = 0,a_1 a_2 a_3 \ldots\;$ also der Wert der Reihe 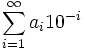$\sum_{i=1}^{\infty} a_i 10^{-i}$ bezeichnet.

Man sagt, dass die Dezimalbruchentwicklung abbricht, wenn die Ziffernfolge ab einer Stelle n nur noch aus Nullen besteht, die dargestellte reelle Zahl also selbst schon ein Dezimalbruch ist. Insbesondere bei allen irrationalen Zahlen bricht die Ziffernfolge nicht ab; es liegt eine unendliche Dezimalbruch-Entwicklung vor.

Zur Umformung periodischer Dezimalbruchentwicklungen (siehe weiter unten) verwendet man die Beziehungen:

$0{,}\overline{1} = \frac{1}{9}; \quad 0{,}\overline{01} = \frac{1}{99}; \quad 0{,}\overline{001} = \frac{1}{999}; \quad \ldots$.

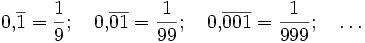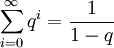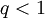Diese Identitäten ergeben sich aus den Rechenregeln für geometrische Reihen, wonach $\sum_{i=0}^{\infty} q^{i} = \frac{1}{1-q}$ für $q < 1\;$ gilt. Im ersten Beispiel wählt man q = 10 ^{− 1} und beginnt die Summation erst beim ersten Folgenglied.

Beispiele:

$0{,}55555\ldots = 0{,}\overline{5} = \frac{5}{9}$

$0{,}33333\ldots = 0{,}\overline{3} = \frac{3}{9} = \frac{1}{3}$

$0{,}424242\ldots = 0{,}\overline{42} = \frac{42}{99} = \frac{14}{33}$

$0{,}081081081\ldots = 0{,}\overline{081} = \frac{81}{999} = \frac{3}{37}$

Die Periode wird jeweils in den Zähler übernommen. Im Nenner stehen so viele Neunen, wie die Periode Stellen hat. Gegebenenfalls sollte der entstandene Bruch noch gekürzt werden.

Etwas komplizierter ist die Rechnung, wenn die Periode nicht unmittelbar auf das Komma folgt:

Beispiele:

$0{,}83333\ldots = 0{,}8\overline{3} = 8{,}\overline{3} : 10 = 8\frac{3}{9} : 10 = 8\frac{1}{3} : 10 = \frac{25}{3} : 10 = \frac{25}{30} = \frac{5}{6}$

$0{,}48363636\ldots = 0{,}48\overline{36} = 48{,}\overline{36} : 100 = 48\frac{36}{99} : 100 = 48\frac{4}{11} : 100 = \frac{532}{11} : 100 = \frac{532}{1100} = \frac{133}{275}$

Doppeldeutigkeit der Darstellung

Eine besondere Eigenschaft bei der Dezimalbruchentwicklung ist, dass eine rationale Zahl zwei unterschiedliche Dezimalbruchentwicklungen besitzen kann. Wie oben beschrieben, kann man 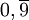$0,\overline{9}$ umformen und zu der Aussage

$0,\overline{9}= \frac{9}{9} = 1$

gelangen.

Diese Identität ist sinnvoll, da zwei reelle Zahlen x und y nur dann verschieden sind, wenn es eine reelle Zahl z gibt, die zwischen ihnen liegt, für die also x < z < y oder y < z < x gilt. Offensichtlich kann im Fall x = 1 und 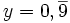$y=0,\overline{9}$ kein solches z existieren.

Aus dieser Identität kann man weiter folgern, dass viele rationale Zahlen (nämlich alle mit endlicher Dezimalbruchentwicklung mit Ausnahme der 0) auf zwei verschiedene Weisen darstellbar sind: entweder eben als endlicher Dezimalbruch mit Periode 0, oder als unendlicher mit Periode 9. Um die Darstellung eindeutig zu machen, kann man die Periode 9 jedoch schlicht verbieten und sich auf endliche Dezimalbrüche beschränken.

Formel

Für periodische Dezimalbrüche mit einer Null vor dem Komma lässt sich folgende Formel aufstellen:

$p = \frac{x \cdot \left(10^n-1\right) + y}{10^m \cdot \left(10^n - 1\right)}$

Dabei sind p die Zahl, x die Zahl vor Beginn der Periode (als Ganzzahl), m die Anzahl der Ziffern vor Beginn der Periode, y die Ziffernfolge der Periode (als Ganzzahl) und n die Länge der Periode.

Die Anwendung dieser Formel soll anhand des letzten Beispiels demonstriert werden:

$p = 0{,}48363636\ldots = 0{,}48\overline{36}$

$x = 48; \quad m = 2; \quad y = 36; \quad n = 2$

$p = \frac{48 \cdot \left(10^2-1\right) + 36}{10^2 \cdot \left(10^2 - 1\right)} = \frac{48 \cdot 99 + 36}{100 \cdot 99} = \frac{4788}{9900} = \frac{133}{275}$

Periode

In der Mathematik bezeichnet man als Periode eines Dezimalbruchs eine Ziffer oder Ziffernfolge, die sich nach dem Komma immer wieder wiederholt. Alle rationalen Zahlen, und nur diese, haben eine periodische Dezimalbruchentwicklung.

Beispiele:

Rein periodische:

1/3 = 0,33333...

1/7 = 0,142857142857...

1/9 = 0,11111...

Gemischt periodische:

2/55 = 0,036363636...

1/30 = 0,03333...

1/6 = 0,16666...

Auch endliche Dezimalbrüche zählen zu den periodischen Dezimalbrüchen; nach Einfügung unendlich vieler Nullen ist zum Beispiel 0,12 = 0,12000...

Echte Perioden (also keine endlichen Dezimalbrüche) treten im Dezimalsystem genau dann auf, wenn sich der Nenner des zugrunde liegenden Bruches nicht ausschließlich durch die Primfaktoren 2 und 5 erzeugen lässt -- 2 und 5 sind die Primfaktoren der Zahl 10, der Basis des Dezimalsystems. Ist der Nenner eine Primzahl P (außer 2 und 5), so hat die Periode höchstens eine Länge, die um eins niedriger ist als der Wert des Nenners (in den Beispielen fett dargestellt).

Die genaue Länge der Periode von 1 / P (falls die Primzahl weder 2 noch 5 ist) entspricht der natürlichen Zahl n, bei der P das erste Mal in der Primfaktorzerlegung von R_n = 10ⁿ − 1 vorkommt.

Beispiel zur Periodenlänge 6: (10⁶ - 1) = 999.999:

999.999 = 3 · 3 · 3 · 7 · 11 · 13 · 37, 1/7 = 0,142857142857... bzw. 1/13 = 0,076923076923....

Sowohl 1/7 als auch 1/13 haben eine Periodenlänge von 6, weil 7 und 13 das erste mal in der Primfaktorzerlegung von R_n = 10⁶ - 1 auftauchen. 1/37 hat jedoch eine Periodenlänge von nur n = 3, weil bereits (10³ - 1) = 999 = 3 · 3 · 3 · 37.

Ist der Nenner keine Primzahl, so ergibt sich die Periodenlänge entsprechend als die Zahl n, bei der der Nenner das erste Mal ein Teiler von R_n = 10ⁿ − 1 ist; die Primfaktoren 2 und 5 des Nenners bleiben dabei unberücksichtigt.

Beispiele: 1/185 = 1/(5·37) hat die gleiche Periodenlänge wie 1/37, nämlich 3.

1/143 = 1/(11·13) hat die Periodenlänge 6, weil 999.999 = 3 · 3 · 3 · 7 · 143 · 37 (siehe oben)

1/260 = 1/(2·2·5·13) hat die gleiche Periodenlänge wie 1/13, also 6.

Notation

Für periodische Dezimalbruchentwicklungen ist eine Schreibweise üblich, bei der der sich periodisch wiederholende Teil der Nachkommastellen durch einen Überstrich markiert wird. Beispiele sind

• $1/6 = 0{,}1\bar{6}$,
• $1/7 = 0{,}\overline{142857}$.

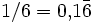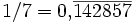Aufgrund technischer Einschränkungen existieren auch andere Konventionen. So kann der Überstrich vorangestellt, eine typografische Hervorhebung (fett, kursiv, unterstrichen) des periodischen Teils gewählt oder dieser in Klammern gesetzt werden:

• 1/6 = 0,1¯6 = 0,16 = 0,16 = 0,16 = 0,1(6)
• 1/7 = 0,¯142857 = 0,142857 = 0,142857 = 0,142857 = 0,(142857)

Nicht periodische Nachkommaziffern-Folge

Wie im Artikel Stellenwertsystem erläutert, besitzen irrationale Zahlen (auch) im Dezimalsystem eine unendliche, nichtperiodische Nachkommaziffern-Folge. Irrationale Zahlen können also nicht durch eine endliche und nicht durch eine periodische Ziffernfolge dargestellt werden. Man kann sich zwar mit endlichen (oder periodischen) Dezimalbrüchen beliebig annähern, jedoch ist eine solche endliche Darstellung niemals exakt. Es ist also nur mithilfe zusätzlicher Symbole möglich, irrationale Zahlen durch endliche Darstellungen anzugeben.

Beispiele solcher Symbole sind Wurzelzeichen, wie für √2, Buchstaben wie π oder e, sowie mathematische Ausdrücke wie unendliche Reihen oder Grenzwerte.

Umrechnung in andere Stellenwertsysteme

Methoden zur Umrechnung von und in das Dezimalsystem werden in den Artikeln zu anderen Stellenwertsystemen und unter Zahlbasiswechsel und Stellenwertsystem beschrieben.

Geschichte

Ohne die Null, aber bereits mit der Dezimalzahlen-Idee (also Zehner, Hunderter, Tausender usw.) rechnete man bereits im Alten Ägypten (siehe Hieroglyphen) und später bei den Römern (siehe römische Zahlen). Die chinesischen Zahlen sind ein Mischsystem aus den Ziffern eins bis neun (eine Null wurde später hinzugefügt) und Zeichen für die Zehnerschritte.

Das Dezimalsystem ist indischer Herkunft, was durch Inschriften und Erwähnungen nachweisbar ist. Die Inder haben die Zahl Null um ca. 600 n.Chr. erfunden und in weiterer Folge das Dezimalsystem entwickelt. Vom Mathematiker und Astronomen Brahmagupta ist aus dem Jahre 628 der früheste bekannte Text über die grundlegenden Rechenvorschriften in diesem Zahlensystem verfasst worden, wie damals in Indien üblich in Versform, die Brahmasphutasiddhanta, auf Deutsch Sindhind. Sein Zeitgenosse Bhaskara I. verwendet 629 die ersten neun Brahmi-Zahlen, von denen unsere Ziffern abstammen, und einen kleinen Kreis für die Null.

Mit der Überarbeitung des Sindhind durch den islamischen Mathematiker Muhammad ibn Musa al-Chwarizmi im 8. Jahrhundert und mit seinem Arithmetikbuch wurde das indische Zahlensystem in der arabischen Welt bekannt. Sein Lehrbuch "Hisab al-dschabr wa-l-muqabala" wurde erst im 12. Jahrhundert ins Lateinische übersetzt und gelangte so nach Europa, wo es durch den Mathematiker Leonardo Fibonacci weiter verbreitet wurde. Auf Reisen hatte er die arabische Mathematik kennengelernt, die er in seinem Rechenbuch "Liber abaci" (Buch des Abakus) vermittelte. Mit ihrer Durchsetzung im 13. Jahrhundert kam auch der Begriff arabische Zahlen auf. In arabischen Ländern werden sie bis heute indische Zahlen genannt.

In Europa verbreitete sich das Rechnen mit den zehn Ziffern sehr langsam und setzte sich erst mit der Erfindung des Buchdrucks durch.

Siehe auch

• Schreibweise von Zahlen
• Zahlbasiswechsel
• Zahlensystem
  • Unärsystem₁
  • Dualsystem₂
  • Ternärsystem₃
  • Quaternärsystem₄
  • Quinärsystem₅
  • Senärsystem₆
  • Oktalsystem₈
  • Duodezimalsystem₁₂
  • Hexadezimalsystem₁₆
  • Vigesimalsystem₂₀
  • Sexagesimalsystem₆₀

Literatur

• Georges Ifrah: Universalgeschichte der Zahlen. 2., durchgesehene u. mit einem Register erweiterte Auflage. Campus-Verlag, Frankfurt/Main 1987, ISBN 3-593-33666-9
• John D. Barrow: Warum die Welt mathematisch ist. Campus-Verlag, Frankfurt/Main 1993, ISBN 3-593-34956-6

Weblinks

• Zahlensysteme im Vergleich
• Umrechnung von Zahlensystemen (Oktal-/Dezimal-/Binär-/Hexadezimalsystem)
• Dezimal-/Zehnersystem für Schüler erklärt auf mathematik-wissen.de

Zahlensysteme

Ägyptisch | Arabisch | Armenisch | Attisch | Babylonisch | Brahmi | Chinesisch | Etruskische | Glagolitisch | Griechisch | Hebräisch | Indisch | Japanisch | Khmer | Koreanisch | Kyrillisch | Maya | Römisch | Sanskrit | Thai