- Distributionentheorie
-
Dieser Artikel erläutert die Distribution als verallgemeinerte Funktion; pfaffsche Systeme werden in der Differentialgeometrie (als eine Verallgemeinerung der exakten Differentialgleichung) auch als geometrische Distribution bezeichnet. 
- Sei
 und
und 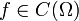 , so ist durch
, so ist durch 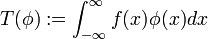 für alle
für alle 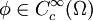 eine Distribution
eine Distribution 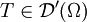 definiert.
definiert. - Sei
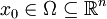 und
und 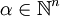 . Dann ist für alle
. Dann ist für alle 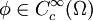 die partielle Ableitung
die partielle Ableitung 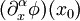 ebenfalls eine Distribution aus
ebenfalls eine Distribution aus 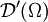 .
. - Die Delta-Distribution, auf welche auch weiter unten eingegangen wird, ist wie der Name schon sagt ebenfalls eine Distribution.
- Der Cauchysche Hauptwert der Funktion
 kann ebenfalls als Distribution T aufgefasst werden. Man setzt
kann ebenfalls als Distribution T aufgefasst werden. Man setzt 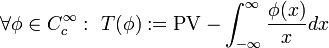 .
.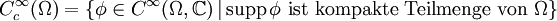
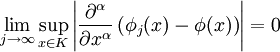

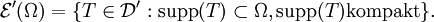
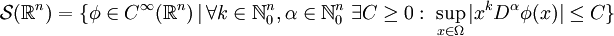
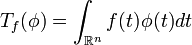
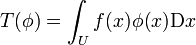
- Hauptartikel: Delta-Distribution


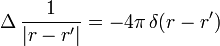
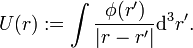
- Δ(r) = − 4πφ(r)
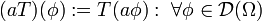 .
.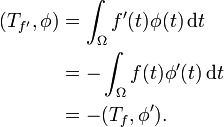
 .
.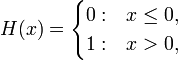
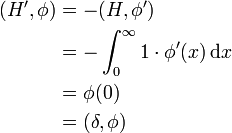
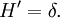

- (u * φ)(x) = u(φ(x − .)).
- Falls u eine glatte Funktion ist, so stimmt die Definition mit der Faltung von Funktionen überein.
- Das Ergebnis der Faltung ist eine glatte Funktion, also gilt
-
 .
.
- Für
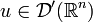 und
und 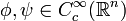 ist die Faltung ist assoziativ, also gilt
ist die Faltung ist assoziativ, also gilt -
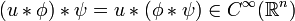 .
.
- Für jeden Multi-Index α gilt für die Ableitung der Faltung
-
 .
.
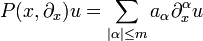
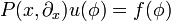
- Hauptartikel: Fundamentallösung
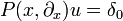
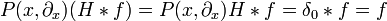
- u = H * f,
- Israel Gelfand: Verallgemeinerte Funktionen (Distributionen). Bände I - III (1958 mit G.E. Schilow), IV (1960 mit N.J. Wilenkin), V (1962 mit M.I. Graev und N.J. Wilenkin), VEB Deutscher Verlag der Wissenschaften, Berlin (Ost).
- Michael James Lighthill: An introduction to Fourier analysis and generalised functions, Cambridge University Press, Cambridge 2003, ISBN 0-521-09128-4.
- Joseph Wloka: Grundräume und Verallgemeinerte Funktionen, Lecture Notes in Mathematics 82, Springer-Verlag 1968, ISBN 3540042504.
Der Begriff der Distribution ist eine Verallgemeinerung des Begriffs der Funktion. Er wurde Mitte des 20. Jahrhunderts von Laurent Schwartz geprägt, der für seine Untersuchung von Distributionen die Fields-Medaille erhielt.
Inhaltsverzeichnis |
Motivation
Entwickelt wurden Distributionen, um gewisse singuläre Objekte der Physik mathematisch behandeln zu können. So ist zum Beispiel die Delta-Distribution geeignet, um Konzepte der theoretischen Physik wie etwa eine „Punktmasse“ oder eine elektromagnetische „Punktladung“ mathematisch zu beschreiben: Von der räumlichen „Dichtefunktion“ eines Massenpunktes mit Einheitsmasse wird gefordert, dass sie überall verschwindet, außer an einem Punkt. Dort muss sie unendlich werden, da das Raumintegral über die Dichtefunktion 1 ergeben soll (Einheitsmasse). Es gibt keine Funktion, die diese Eigenschaften der Dichte erfüllt; wenn man aber das Integral als Funktional auffasst, kann man die Dichte als Delta-Distribution beschreiben.
Distributionen sind heutzutage ein unentbehrliches Mittel in vielen Gebieten der Mathematik, Physik und Elektrotechnik, zum Beispiel in der Theorie der partiellen Differentialgleichungen sowie der Fourieranalyse, die wiederum eine prominente Rolle in der Quantenelektrodynamik und der Signalverarbeitung spielen.
Definitionen
Definition von Distributionen
Eine Distribution ist eine stetige und lineare Abbildung von einem Testfunktionenraum in die komplexen Zahlen (siehe Funktional). Das bedeutet, dass eine Distribution eine Abbildung ist, die jeder Testfunktion eine Zahl zuordnet. Die Menge der Distributionen mit den entsprechenden Verknüpfungen ist also der topologische Dualraum zum Testfunktionenraum.
Schreibweise für Distributionen
Nach der Definition ordnet eine Distribution jeder Testfunktion eine Zahl zu:
In der letzten Gleichung ist 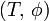 einfach eine Schreibweise für den Wert, den die Distribution der Testfunktion
einfach eine Schreibweise für den Wert, den die Distribution der Testfunktion 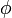 zuordnet. Man sagt: Die Distribution
zuordnet. Man sagt: Die Distribution 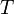 wird auf
wird auf 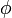 angewendet.
angewendet.
Beispiele
Testfunktionen
Es gibt mehrere Räume von Testfunktionen, wir wollen hier drei bekannte Räume beschreiben.
Wir bezeichnen mit
die Menge aller unendlich oft differenzierbaren Funktionen, welche einen kompakten Träger haben, also außerhalb eines kompakten Bereichs gleich null sind.
Testfunktionen für allgemeine Distributionen
Für den ersten Testfunktionenraum, den man mit 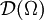 bezeichnet, benötigt man noch einen Konvergenzbegriff. Man sagt eine Folge
bezeichnet, benötigt man noch einen Konvergenzbegriff. Man sagt eine Folge 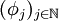 mit
mit  konvergiert gegen
konvergiert gegen 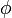 , wenn es ein Kompaktum
, wenn es ein Kompaktum 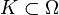 gibt mit
gibt mit 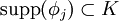 für alle j und
für alle j und
für alle Multiindizes 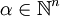 . Der Raum
. Der Raum 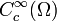 zusammen mit diesem Konvergenzbegriff ergibt einen lokal-konvexen Raum, den man mit
zusammen mit diesem Konvergenzbegriff ergibt einen lokal-konvexen Raum, den man mit 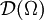 bezeichnet.
bezeichnet.
Testfunktionen für Distributionen mit kompaktem Träger
Ein weiterer Testfunktionenraum ist der Raum der glatten Funktionen 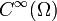 . Dieser Testfunktionenraum zusammen mit der folgenden Familie von Halbnormen und der damit induzierten Topologie wird mit
. Dieser Testfunktionenraum zusammen mit der folgenden Familie von Halbnormen und der damit induzierten Topologie wird mit 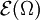 bezeichnet. Die Familie von Halbnormen lautet
bezeichnet. Die Familie von Halbnormen lautet
Diese induziert eine lokal-konvexe Topologie. Hierbei ist  und
und 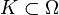 durchläuft alle Kompakta. Der Raum der Distributionen, welcher durch
durchläuft alle Kompakta. Der Raum der Distributionen, welcher durch 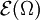 erzeugt wird, wird mit
erzeugt wird, wird mit 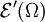 bezeichnet und heißt Raum der Distributionen mit kompaktem Träger, da gilt
bezeichnet und heißt Raum der Distributionen mit kompaktem Träger, da gilt
Dies ist der topologische Dualraum zu 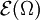 .
.
Raum der schnell fallenden Funktionen
Hauptartikel: Schwartz-Raum
Der dritte Testfunktionenraum, der hier beschrieben wird, sind die sogenannten schnell fallenden Funktionen. Im Unterschied zu den vorhergehenden werden diese meist dann verwendet, wenn Distributionen auf unbeschränkten Gebieten benötigt werden. Schnell fallende Funktionen sind unendlich oft differenzierbar und streben im Unendlichen so schnell gegen 0, dass sie und alle ihre Ableitungen multipliziert mit einer beliebigen Potenz immer noch gegen 0 gehen. Die Menge all dieser Testfunktionen wird als Schwartz-Raum 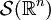 bezeichnet:
bezeichnet:
Dieser Raum ist unter der Fourier-Transformation invariant und in allen Sobolew-Räumen enthalten. Die mit diesen Testfunktionen definierten Distributionen nennt man temperierte oder auch langsam wachsende Distributionen und schreibt 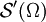 . (Hierbei benutzt man, dass die Eigenschaft des Langsamen Wachstums bei den Distributionen dual zum Schnell Fallend bei den Testfunktionen ist.)
. (Hierbei benutzt man, dass die Eigenschaft des Langsamen Wachstums bei den Distributionen dual zum Schnell Fallend bei den Testfunktionen ist.)
Die wesentliche Eigenschaft der Schwartzfunktionen ist, dass sie Fourier-transformierbar sind und dass die Fouriertransformation ein Isomorphismus auf 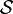 ist.
ist.
Regulärität und singulärer Träger
Reguläre Distributionen
Reguläre Distributionen lassen sich als Integraloperatoren Tf schreiben, was bedeutet es gibt eine Darstellung
mit  eine lokal integrierbare Funktion. Nicht alle Distributionen lassen sich auf diese Weise schreiben, weil es nicht immer eine solche Funktion f gibt. Würde man zum Beispiel die Delta-Distribution als reguläre Distribution annehmen, erhält man den Widerspruch δ = 0 (als Distribution).
eine lokal integrierbare Funktion. Nicht alle Distributionen lassen sich auf diese Weise schreiben, weil es nicht immer eine solche Funktion f gibt. Würde man zum Beispiel die Delta-Distribution als reguläre Distribution annehmen, erhält man den Widerspruch δ = 0 (als Distribution).
In der Praxis verwendet man jedoch diese Schreibweise auch für nicht reguläre Distributionen. Jedoch muss einem dabei bewusst sein, dass dies nur eine Schreibweise ist.
Träger
Sei 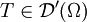 eine Distribution. Man sagt, dass ein Punkt
eine Distribution. Man sagt, dass ein Punkt 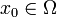 zum Träger von T gehört (
zum Träger von T gehört (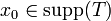 ), wenn für jede offene Umgebung
), wenn für jede offene Umgebung 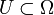 von x0 eine Funktion
von x0 eine Funktion 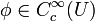 existiert mit
existiert mit 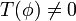 .
.
Falls T eine reguläre Distribution ist, so ist diese Definition äquivalent zur Definition des Trägers einer Funktion.
Singulärer Träger
Sei 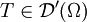 eine Distribution. Man sagt, dass ein Punkt
eine Distribution. Man sagt, dass ein Punkt 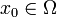 nicht zum singulären Träger gehört, wenn es eine offene Umgebung
nicht zum singulären Träger gehört, wenn es eine offene Umgebung 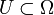 von x0 und eine Funktion
von x0 und eine Funktion  gibt mit
gibt mit
für alle 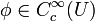 .
.
Es gilt also 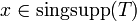 genau dann, wenn es keine offene Umgebung U von x0 gibt, sodass die Einschränkung von T auf U gleich einer glatten Funktion ist. Insbesondere ist der singuläre Träger einer nicht regulären Distribution nicht leer.
genau dann, wenn es keine offene Umgebung U von x0 gibt, sodass die Einschränkung von T auf U gleich einer glatten Funktion ist. Insbesondere ist der singuläre Träger einer nicht regulären Distribution nicht leer.
Beispiel
Delta-Distribution
Die Delta-Distribution δ ist eine irreguläre Distribution. Das heißt sie kann nicht durch eine gewöhnliche Funktion dargestellt werden, obwohl sie oft wie eine solche geschrieben wird. Es gilt:
Sprich: Die Delta-Distribution angewendet auf eine Testfunktion φ ergibt die Testfunktion ausgewertet an der Stelle 0.
Dies ist ein Spezialfall der folgenden allgemeineren Definition mit 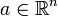 :
:
Die Schreibweise „wie eine gewöhnliche Funktion“ ist δa(t) = δ(t − a).
Poisson-Gleichung
Ein prominentes Beispiel ist die formale Identität
aus der Elektrostatik, die im Zusammenhang mit Integral
auftritt. Man kann die oben angegebene Identität benutzen, um nachzuweisen, dass U die sog. Poisson-Gleichung
löst. Δ ist der Laplace-Operator. Bei Verwendung von Distributionen, d.h. bei Differentiation unter dem Integral, erhält man mit den Eigenschaften der unten ausführlich behandelten Delta-Distribution δ(r − r') sehr schnell eine sog. „schwache Lösung“, die dann gegebenenfalls noch „regularisiert“ werden kann (z. B.: wenn φ stetig ist, ist U zweimal stetig differenzierbar und erfüllt die Poisson-Gleichung im gewöhnlichen Sinn).
Operationen auf Distributionen
Da die drei zu Anfang behandelten Distributionenräume Vektorräume sind, sind die Addition von Distributionen und die Multiplikation einer komplexen Zahl mit einer Distribution schon definiert. Im Folgenden werden noch die Multiplikation einer Funktion mit einer Distribution die Ableitung einer Distribution und die Faltung einer Distribution mit einer glatten funktion definiert.
Multiplikation mit einer Funktion
Sei 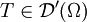 und
und 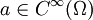 . Dann wird die Distribution
. Dann wird die Distribution 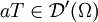 definiert als
definiert als
Differentiation
Motivation
Betrachtet man eine stetig differenzierbare Funktion f und die ihr zugeordnete reguläre Distribution Tf, so erhält man die Rechenregel
Hierbei wurde partielle Integration verwendet, wobei die Randterme wegen der gewählten Eigenschaften der Testfunktion φ wegfallen. Dies entspricht der schwachen Ableitung. Die äußeren beiden Terme sind auch für singuläre Distributionen definiert, und man verwendet dies zur Definition der Ableitung einer beliebigen Distribution T.
Definition
Sei also 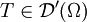 eine Distribution und
eine Distribution und 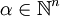 . Dann wird eine Distribution
. Dann wird eine Distribution 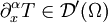 definiert als
definiert als
Beispiel
Die Heaviside-Funktion 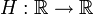 ist durch
ist durch
definiert. Sie ist mit Ausnahme von x = 0 überall differenzierbar. Man kann sie als reguläre Distribution betrachten, und die Rechnung
zeigt, dass ihre Ableitung (als Distribution) die Delta-Distribution ist:
Man kann außerdem die Delta-Distribution selbst noch ableiten:
Die Ableitungen der Delta-Distribution sind also ( bis auf den zusätzlichen Vorzeichenfaktor ( − 1)n ) gleich den Ableitungen der Testfunktion an der Stelle 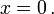
Faltung mit einer Funktion
Definition
Sei 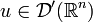 eine Distribution und
eine Distribution und 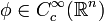 eine Funktion so ist die Faltung definiert durch
eine Funktion so ist die Faltung definiert durch
Eigenschaften
Differentialgleichungen
Lösungen im Distributionensinne
Sei
ein Differentialoperator mit glatten Koeffizientenfunktionen 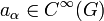 . Eine Distribution
. Eine Distribution  heißt Distributionenlösung von
heißt Distributionenlösung von 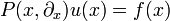 , falls die von
, falls die von 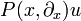 und f erzeugten Distributionen übereinstimmen. Dies bedeutet
und f erzeugten Distributionen übereinstimmen. Dies bedeutet
für alle 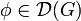 . Falls die Distribution u regulär und sogar m-mal stetig differenzierbar ist, dann ist u ein klassische Lösung der Differentialgleichung.
. Falls die Distribution u regulär und sogar m-mal stetig differenzierbar ist, dann ist u ein klassische Lösung der Differentialgleichung.
Fundamentallösungen
Sei 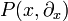 nun ein linearer Differentialoperator. Eine Distribution
nun ein linearer Differentialoperator. Eine Distribution 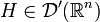 heißt Fundamentallösung, falls H die Differentialgleichung
heißt Fundamentallösung, falls H die Differentialgleichung
im Distributionensinne löst.
Die Menge aller Fundamentallösungen von 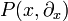 ergibt sich durch Addition einer speziellen Fundamentallösung H mit der allgemeinen homogenen Lösungen H0. Die allgemeine homogene Lösung ist die Menge der Distributionen für die
ergibt sich durch Addition einer speziellen Fundamentallösung H mit der allgemeinen homogenen Lösungen H0. Die allgemeine homogene Lösung ist die Menge der Distributionen für die 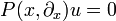 gilt. Nach einem Satz von Bernard Malgrange besitzt jeder lineare Differentialoperator mit konstanten Koeffizienten eine Fundamentallösung
gilt. Nach einem Satz von Bernard Malgrange besitzt jeder lineare Differentialoperator mit konstanten Koeffizienten eine Fundamentallösung 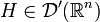 .
.
Mit Hilfe dieser Fundamentallösungen erhällt man durch Faltung Lösungen entsprechender inhomogener Differentialgleichungen. Sei f eine glatte Funktion (oder allgemeiner eine Distribution mit kompaktem Träger), dann ergibt sich wegen
eine Lösung von 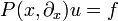 in der Form
in der Form
wobei 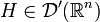 genauso wie oben eine Fundamentallösung des Differentialoperators ist.
genauso wie oben eine Fundamentallösung des Differentialoperators ist.
Literatur
Wikimedia Foundation.
