- Pfaffsche Form
-
Im mathematischen Teilgebiet der Differentialgeometrie bezeichnet Pfaffsche Form (nach Johann Friedrich Pfaff[1]) oder Differentialform vom Grad 1 oder kurz 1-Form ein Objekt, das in gewisser Weise dual zu einem Vektorfeld ist. Pfaffsche Formen sind die natürlichen Integranden für Wegintegrale.
Kontext
Es sei U
- eine offene Teilmenge des

- oder allgemeiner ein offener Teil einer differenzierbaren Untermannigfaltigkeit des

- oder allgemein ein offener Teil einer (abstrakten) differenzierbaren Mannigfaltigkeit.
In jedem dieser Fälle gibt es
- den Begriff der differenzierbaren Funktion auf U; der Raum der differenzierbaren Funktionen auf U werde mit
 bezeichnet;
bezeichnet; - den Begriff des Tangentialraums TpU an U in einem Punkt
 ;
; - den Begriff der Richtungsableitung Xf für einen Tangentialvektor
 und eine differenzierbare Funktion f;
und eine differenzierbare Funktion f; - den Begriff des differenzierbaren Vektorfeldes auf U. Der Raum der Vektorfelder auf U sei mit ΓTU bezeichnet.
Elementare Definition
Eine pfaffsche Form ω auf U ordnet jedem Punkt
 eine Linearform
eine Linearform  zu. Derartige Linearformen heißen Kotangentialvektoren; sie sind Elemente des Dualraumes
zu. Derartige Linearformen heißen Kotangentialvektoren; sie sind Elemente des Dualraumes  des Tangentialraumes TpU. Der Raum
des Tangentialraumes TpU. Der Raum  wird Kotangentialraum genannt.
wird Kotangentialraum genannt.Eine pfaffsche Form ω ist also eine Abbildung
Andere Definitionen
- Eine differenzierbare pfaffsche Form ist eine
 -lineare Abbildung
-lineare Abbildung  Stetige oder messbare pfaffsche Formen sind analog definiert.
Stetige oder messbare pfaffsche Formen sind analog definiert. - Die oben gegebene Menge
 wird als Kotangentialbündel bezeichnet. Das ist nichts anderes als das duale Vektorbündel des Tangentialbündels. Eine pfaffsche Form kann damit als Schnitt des Kotangentialbündels definiert werden.
wird als Kotangentialbündel bezeichnet. Das ist nichts anderes als das duale Vektorbündel des Tangentialbündels. Eine pfaffsche Form kann damit als Schnitt des Kotangentialbündels definiert werden.
Totales Differential einer Funktion
Das totale Differential oder die äußere Ableitung df einer differenzierbaren Funktion
 ist die pfaffsche Form, die folgendermaßen definiert ist: Ist
ist die pfaffsche Form, die folgendermaßen definiert ist: Ist  ein Tangentialvektor, so ist: (df)p(X) = Xf, also gleich der Richtungsableitung von f in Richtung X.
ein Tangentialvektor, so ist: (df)p(X) = Xf, also gleich der Richtungsableitung von f in Richtung X.Ist also
 ein Weg mit γ(0) = p und
ein Weg mit γ(0) = p und  , so ist
, so istEs gilt:
- dλ = 0, falls
 eine konstante Funktion ist;
eine konstante Funktion ist;  für differenzierbare Funktionen
für differenzierbare Funktionen  .
.
Ist auf U ein Skalarprodukt
 gegeben, so lässt sich das totale Differential von f mit Hilfe des Gradienten darstellen:
gegeben, so lässt sich das totale Differential von f mit Hilfe des Gradienten darstellen:Koordinatendarstellung
Es sei
 ein Koordinatensystem auf U. Die Koordinaten können als Funktionen
ein Koordinatensystem auf U. Die Koordinaten können als Funktionenaufgefasst werden, die einem Punkt seine i-te Koordinate zuordnen. Die totalen Differentiale
 dieser Funktionen bilden eine lokale Basis. Das heißt, für jeden Punkt
dieser Funktionen bilden eine lokale Basis. Das heißt, für jeden Punkt  ist
isteine Basis von
 .
.Damit lässt sich jede pfaffsche Form auf eindeutige Weise als
mit Funktionen
 schreiben.
schreiben.
Die äußere Ableitung einer beliebigen differenzierbaren Funktion hat die Darstellung
hat die DarstellungDefinition des Kurvenintegrals
Es sei
![\varphi\colon[a,b]\rightarrow U](5/80541e98e2d6cfba2de008e5dffe3e6a.png) ein stetig differenzierbarer Weg in U und ω eine 1-Form auf U. Dann ist das Integral von ω entlang φ definiert als:
ein stetig differenzierbarer Weg in U und ω eine 1-Form auf U. Dann ist das Integral von ω entlang φ definiert als:Dabei bezeichnet
 die Ableitung von φ nach dem Parameter t.
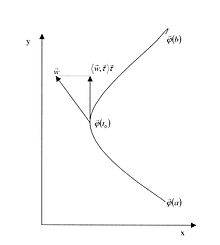
die Ableitung von φ nach dem Parameter t.Geometrische Interpretation des Kurvenintegrals
Eine stetig differenzierbare Funktion
![\varphi\colon[a,b]\to\R^3](9/c49949be377f1c2013030176217740fd.png) stellt die Parametrisierung einer Raumkurve dar. Der Parameter
stellt die Parametrisierung einer Raumkurve dar. Der Parameter ![t\in[a,b]](e/c9ef8c742260828c469822e9c5dbe2c9.png) kann als Zeitparameter aufgefasst werden. Zum Zeitpunkt t = a befindet man sich am Ort φ(a). Dann wird entlang einer bestimmten Bahn oder Kurve zum Ort φ(b) gefahren. Also zum Zeitpunkt t = b ist der Endpunkt φ(b) der Kurve erreicht. Wird zu jedem Zeitpunkt t der Ort des Überfahrens notiert, so ergibt sich die Abbildung
kann als Zeitparameter aufgefasst werden. Zum Zeitpunkt t = a befindet man sich am Ort φ(a). Dann wird entlang einer bestimmten Bahn oder Kurve zum Ort φ(b) gefahren. Also zum Zeitpunkt t = b ist der Endpunkt φ(b) der Kurve erreicht. Wird zu jedem Zeitpunkt t der Ort des Überfahrens notiert, so ergibt sich die Abbildung ![\varphi\colon[a,b]\rightarrow\R^3](5/90574868ebd759ca279766b87f31fef0.png) .
.Es ist anschaulich klar, dass dieselbe Kurve auf unterschiedliche Weise überfahren werden kann. So ist konstante Geschwindigkeit eine Möglichkeit. Eine weitere ergibt sich aus einem langsamen Start und mit anschließender Beschleunigung. Für dieselbe Kurve gibt es unterschiedliche Parametrisierungen. Die Bezeichnung „Kurvenintegral“ ist deshalb gerechtfertigt, weil gezeigt werden kann, dass der Wert des Integrals unabhängig von der gewählten Parametrisierung der Kurve ist. Mit einer Ausnahme: Wird der Anfangs- und Endpunkt der Kurve vertauscht, also erfolgt die Bewegung vom Endpunkt zurück zum Anfangspunkt der Kurve, so ändert sich das Vorzeichen (+,-) des Integrals.
Im Anschauungsraum
 können Tangential- und Kotangentialvektoren mithilfe des Skalarproduktes miteinander identifiziert werden: Einem Kotangentialvektor ω entspricht der Vektor
können Tangential- und Kotangentialvektoren mithilfe des Skalarproduktes miteinander identifiziert werden: Einem Kotangentialvektor ω entspricht der Vektor  , für den
, für den für alle
für alle 
gilt. So können 1-Formen mit Vektorfeldern identifiziert werden.
Dem Integral einer 1-Form entspricht das (gewöhnliche) Integral über das Skalarprodukt mit dem Tangentenvektor:
Ist die Kurve nach der Bogenlänge parametrisiert, so ist der Integrand die (gerichtete) Länge der Projektion des Vektors
 auf die Tangente an die Kurve:
auf die Tangente an die Kurve:Exakte und geschlossene Formen
Eine stetig differenzierbare Funktion
 heißt Stammfunktion der 1-Form ω, wenn gilt:
heißt Stammfunktion der 1-Form ω, wenn gilt:- dF = ω.
Eine 1-Form heißt exakt, wenn sie eine Stammfunktion besitzt.
Eine 1-Form
 heißt geschlossen, wenn gilt:
heißt geschlossen, wenn gilt: für alle i,j.
für alle i,j.
Allgemeiner kann ein totales Differential definiert werden, das jeder 1-Form eine 2-Form dω zuordnet. Eine Form heißt genau dann geschlossen, wenn dω = 0 gilt. Aus dem Satz von Schwarz folgt, dass jede exakte Form geschlossen ist.
Kurvenintegral des totalen Differentials
Für das Kurvenintegral des totalen Differentials dF entlang eines Weges
![\varphi\colon[a,b]\to U](3/1a3b6cb6446f22a5ec9d10b37f74778c.png) gilt:
gilt:∫ dF = F(φ(b)) − F(φ(a)). φ Das Integral des totalen Differentials hängt also nicht von der Kurvenform, sondern nur von den Endpunkten der Kurve ab. Das Integral über eine geschlossene Kurve, also φ(a) = φ(b), ist somit gleich Null:
Im Spezialfall
 und φ(t) = t ergibt sich der Fundamentalsatz der Analysis, da das Integral auf der linken Seite
und φ(t) = t ergibt sich der Fundamentalsatz der Analysis, da das Integral auf der linken Seiteist. Die obigen Aussagen lassen sich direkt auf den Fundamentalsatz zurückführen.
Existenz einer Stammfunktion
- Wie bereits erwähnt, ist Geschlossenheit eine notwendige Bedingung für Exaktheit. Das Poincaré-Lemma besagt, dass die Hindernisse für die Umkehrung globaler Natur sind: In einem einfach zusammenhängenden, insbesondere in jedem sternförmigen Gebiet
 besitzt jede geschlossene Pfaffsche Form eine Stammfunktion. Insbesondere ist jede geschlossene pfaffsche Form lokal exakt.
besitzt jede geschlossene Pfaffsche Form eine Stammfunktion. Insbesondere ist jede geschlossene pfaffsche Form lokal exakt.
- Eine stetige Pfaffsche Form ω auf einem Gebiet
 besitzt genau dann eine Stammfunktion, wenn das Integral von ω entlang jeder geschlossenen Kurve φ in U verschwindet.
besitzt genau dann eine Stammfunktion, wenn das Integral von ω entlang jeder geschlossenen Kurve φ in U verschwindet.
Physikalische Beispiele für Pfaffsche Formen
Erstes Beispiel „Kraftfeld“
Ein Kraftfeld beschreibt die Kraft, die auf einen Gegenstand an einem beliebigen Ort
 ausgeübt wird. Beispielsweise bewegt sich die Erde im Kraftfeld der Sonne. Das Kraftfeld ordnet jedem Punkt
ausgeübt wird. Beispielsweise bewegt sich die Erde im Kraftfeld der Sonne. Das Kraftfeld ordnet jedem Punkt  einen Kraftvektor
einen Kraftvektor  zu. Jedem Kraftvektor
zu. Jedem Kraftvektor  kann eine lineare Abbildung
kann eine lineare Abbildung  zugeordnet werden, die mittels des Skalarproduktes
zugeordnet werden, die mittels des Skalarproduktes  einen beliebigen Vektor
einen beliebigen Vektor  linear auf den Zahlenkörper
linear auf den Zahlenkörper  abbildet. Aufgrund dieser Interpretation kann das Kraftfeld als Pfaffsche Form oder Differentialform 1. Ordnung verstanden werden.
abbildet. Aufgrund dieser Interpretation kann das Kraftfeld als Pfaffsche Form oder Differentialform 1. Ordnung verstanden werden.Wird das Kraftfeld in kartesischen Koordinaten dargestellt, wobei
 mit i=1,2 oder 3 die Einheitsvektoren in kartesischen Koordinaten sind, so gilt für die Koordinatendarstellung der Pfaffschen Form:
mit i=1,2 oder 3 die Einheitsvektoren in kartesischen Koordinaten sind, so gilt für die Koordinatendarstellung der Pfaffschen Form: .
.Die Differentiale dxi sind einfach die entsprechenden Basisvektoren des Dualraums, also:
 .
.Es muss Arbeit geleistet werden, um einen Gegenstand in einem Kraftfeld entlang eines Weges
![\vec\varphi:\left[a,b\right]\rightarrow \mathbb{R}^3](5/2e529a148da8743c9b72d3fd9ba98ad4.png) von einem Ort
von einem Ort  zu einem Ort
zu einem Ort  zu bewegen. Die Größe W der geleisteten Arbeit ist gegeben durch das Kurvenintegral entlang des Weges:
zu bewegen. Die Größe W der geleisteten Arbeit ist gegeben durch das Kurvenintegral entlang des Weges:
In einem konservativen Kraftfeld ist die Größe W der geleisteten Arbeit wegunabhängig. Eine konservative Kraft leistet auf einem geschlossenen Weg keine Arbeit.
Die Stammfunktion V eines konservativen Kraftfeldes wird Potential oder potentielle Energie der Kraft
 genannt. Also stellt das totale Differential des Potentials V wiederum die Kraft
genannt. Also stellt das totale Differential des Potentials V wiederum die Kraft  dar. Es gilt:
dar. Es gilt:
Das Vorzeichen ist lediglich Konvention.
Zweites Beispiel „Entropie“
Eine weitere wichtige Anwendung der Theorie der Differentialformen liegt im Bereich der Thermodynamik. Gemäß der Clausiuschen Ungleichung gilt:

T stellt die Temperatur des thermodynamischen Systems und δQ den Wärmeaustauschkontakt des Systems mit seiner Umgebung dar. Das thermodynamische System kann beispielsweise ein Gas darstellen, dessen unabhängige Zustandsgrößen Temperatur T, Druck P und Volumen V des Gases sind. Die Koordinatendarstellung des Wärmeaustauschkontakts ist damit gegeben durch:
 .
.Das vorstehende Integral wird entlang eines geschlossenen Weges c im dreidimensionalen Zustandsraum (P,V,T) gebildet. Ein geschlossener Weg c im Zustandsraum wird in der Thermodynamik Kreisprozess genannt. Die Differentialform
 besitzt genau dann eine Stammfunktion, wenn jeder Kreisprozess reversibel ist:
besitzt genau dann eine Stammfunktion, wenn jeder Kreisprozess reversibel ist:
In diesem Fall besitzt die Pfaffsche Form
 eine Stammfunktion S, die Entropie genannt wird. Für reversible Kreisprozesse gilt:
eine Stammfunktion S, die Entropie genannt wird. Für reversible Kreisprozesse gilt:
1/T stellt einen integrierenden Faktor dar, der aus der Differentialform
 ein totales Differential
ein totales Differential  erzeugt.
erzeugt.Hieraus folgt der zweite Hauptsatz der Thermodynamik:
 oder
oder 
In einem isolierten System gibt es keinen Wärmeaustausch mit der Umgebung, weshalb gilt
 . Es folgt aus dem zweite Hauptsatz, dass die Entropie eines isolierten Systems nicht abnehmen kann.
. Es folgt aus dem zweite Hauptsatz, dass die Entropie eines isolierten Systems nicht abnehmen kann.Literatur
- Otto Forster: Analysis 3. 3. Auflage, vieweg studium, 1984
- Martin Schottenloher: Geometrie und Symmetrie in der Physik, vieweg Lehrbuch, 1995
Einzelnachweise
- ↑ vgl. Günther J. Wirsching: Gewöhnliche Differentialgleichungen. Eine Einführung mit Beispielen, Aufgaben und Musterlösungen. Teubner Verlag, Wiesbaden 2006, ISBN 3-519-00515-8, S. 63 (online)
- eine offene Teilmenge des
Wikimedia Foundation.