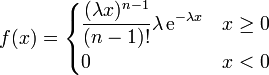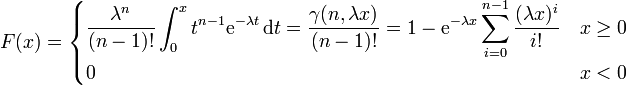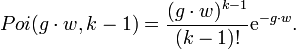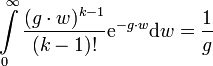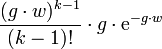- Erlangverteilung
-
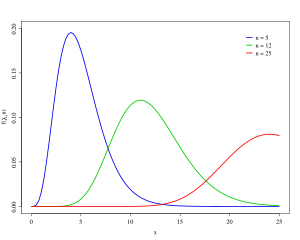
Die Erlang-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung. Sie wurde von Agner Krarup Erlang für die statistische Modellierung der Intervall-Längen zwischen Telefonanrufen entwickelt.
Die Erlang-Verteilung wird vor allem in der Warteschlangentheorie verwendet, um die Verteilung der Zeitspanne zwischen Ereignissen eines Poisson-Prozesses, beispielsweise der Ankunft von Kunden, zu erfassen, sowie in der Qualitätssicherung zur Beschreibung von Lebensdauern. Anwendbar ist diese Verteilung insbesondere für die Planung der Anzahl der in einem Callcenter benötigten Agents in einem Zeitintervall, d. h. für die Personaleinsatzplanung.
Inhaltsverzeichnis
Definition
Die Erlang-Verteilung
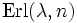 mit den Parametern λ (einer reellen Zahl) und
mit den Parametern λ (einer reellen Zahl) und 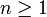 (einer natürlichen Zahl) ist eine spezielle Gammaverteilung, die durch die Dichtefunktion
(einer natürlichen Zahl) ist eine spezielle Gammaverteilung, die durch die Dichtefunktionfestgelegt wird, und die sich von der allgemeinen Gammaverteilung durch die Beschränkung auf natürliche Zahlen im zweiten Parameter unterscheidet.
Die Wahrscheinlichkeit, dass
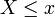 ist, ist durch die Verteilungsfunktion
ist, ist durch die Verteilungsfunktiongegeben, wobei γ die unvollständige Gammafunktion bezeichnet.
Herleitung
Sei w eine Orts- oder Zeitvariable und g die kleine konstante Eintretenshäufigkeit von Ereignissen im Einheitsintervall von w. Gesucht ist die Verteilung der Größe des Abstandes w bis zum Eintreten des k-ten Ereignisses, oder anders formuliert: Wie ist die Größe der möglichen w-Bereiche für k-1 bereits eingetretene Ereignisse verteilt ?
Diese Verteilung ergibt sich aus der Poisson-Verteilung: die Wahrscheinlichkeit für das Eintreten von k-1 Ereignissen innerhalb eines Bereichs w ist
Betrachtet man nun diesen Ausdruck nicht mehr bei festem Bereich w als Funktion für die Wahrscheinlichkeit von k-1 Ereignissen, sondern bei gegebenem k als Funktion für die Wahrscheinlichkeit der Bereichsgröße w, so entsteht nach der noch notwendigen Normierung (Summe über alle Wahrscheinlichkeiten gleich eins)
die Wahrscheinlichkeitsdichte
der Erlang-Verteilung.
Eigenschaften
Erwartungswert
Die Erlang-Verteilung besitzt den Erwartungswert
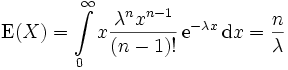 .
.
Varianz
Analog ergibt sich die Varianz zu
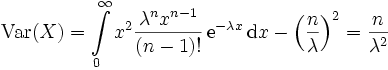 .
.
Beziehungen zu anderen Verteilungen
Beziehung zur Exponentialverteilung
- Die Erlang-Verteilung
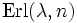 ist eine Verallgemeinerung der Exponentialverteilung, denn sie geht für n = 1 in diese über
ist eine Verallgemeinerung der Exponentialverteilung, denn sie geht für n = 1 in diese über 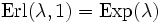 .
. - Es seien n viele, alle mit dem gleichen Parameter λ exponentialverteilte Zufallsvariablen
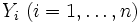 , die stochastisch unabhängig sind, gegeben. Dann ist die Zufallsvariable
, die stochastisch unabhängig sind, gegeben. Dann ist die Zufallsvariable 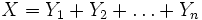 Erlang-verteilt mit den Parametern n und λ
Erlang-verteilt mit den Parametern n und λ 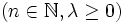 .
.
Beziehung zur Poisson-Verteilung
- Für einen Poisson-Prozess wird die zufällige Anzahl der Ereignisse bis zu einem definierten Zeitpunkt mittels Poisson-Verteilung
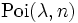 bestimmt, die zufällige Zeit bis zum n-ten Ereignis ist Erlang-verteilt. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über, mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann.
bestimmt, die zufällige Zeit bis zum n-ten Ereignis ist Erlang-verteilt. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über, mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann. - Die Erlang-Verteilung ist die zur Poisson-Verteilung konjugierte Verteilung.
- Für die Verteilungsfunktionen der Erlang-Verteilung und der Poisson-Verteilung gilt
- FErlang(n + 1) + FPoisson(n) = 1.
Beziehung zur stetigen Gleichverteilung
Eine Erlang-Verteilung kann als Faltung von n gleichmäßig stetig verteilten Funktionen X(0,1) erzeugt werden
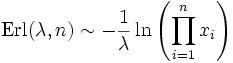 .
.
Wikimedia Foundation.