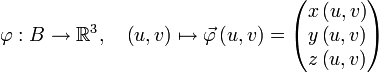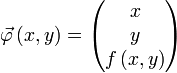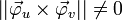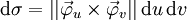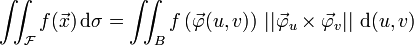- Flächenintegral
-
Das Oberflächenintegral oder Flächenintegral ist eine Verallgemeinerung des Integralbegriffes auf ebenen oder gekrümmten Flächen. Integrationsgebiet
 ist also nicht ein eindimensionales Intervall, sondern eine zweidimensionale Menge im dreidimensionalen Raum
ist also nicht ein eindimensionales Intervall, sondern eine zweidimensionale Menge im dreidimensionalen Raum  . Für eine allgemeinere Darstellung im
. Für eine allgemeinere Darstellung im  mit
mit 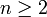 siehe: Integration auf Mannigfaltigkeiten.
siehe: Integration auf Mannigfaltigkeiten.Es wird generell zwischen einem skalaren und einem vektoriellen Oberflächenintegral unterschieden, je nach Form des Integranden und des sogenannten Oberflächenelements. Sie lauten
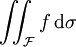 mit skalarer Funktion f und skalarem Oberflächenelement dσ sowie
mit skalarer Funktion f und skalarem Oberflächenelement dσ sowie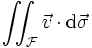 mit vektorwertiger Funktion
mit vektorwertiger Funktion 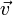 und vektoriellem Oberflächenelement
und vektoriellem Oberflächenelement 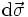 .
.
Inhaltsverzeichnis
Begriffe und Definitionen
Bei der Integration über Flächen treten Parametrisierungen der Fläche an die Stelle der Integrationsvariable und Oberflächenelemente an die Stelle der infinitesimalen (unendlich kleinen) Intervallbreite dx.
Parametrisierung
Als zweidimensionale Menge lässt sich eine Oberfläche als Funktion von zwei Variablen darstellen (parametrisieren). Ist
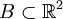 eine Menge, deren Rand keine doppelten Punkte enthält, stetig differenzierbar, nicht unendlich lang und ferner
eine Menge, deren Rand keine doppelten Punkte enthält, stetig differenzierbar, nicht unendlich lang und ferner  eine Abbildung von B in den
eine Abbildung von B in den 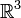 ist, so sagt man,
ist, so sagt man,  ist Parametrisierung der Fläche
ist Parametrisierung der Fläche  , wenn
, wenn 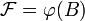 ist.
ist.Allgemein lässt sich eine Fläche im
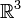 mit zwei Parametern u und v in folgender Form darstellen:
mit zwei Parametern u und v in folgender Form darstellen:- Beispiel 1: Die Oberfläche einer Kugel mit Radius R lässt sich wie folgt parametrisieren: B ist das Rechteck
![[0, \pi] \times [0, 2\pi]](/pictures/dewiki/101/ec5949809a3043d4ff15ee2d5c584eac.png) und
und
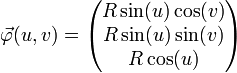 .
.
Man rechnet leicht nach, dass diese Parametrisierung die Kugelgleichung x2 + y2 + z2 = R2 erfüllt (siehe auch Kugelkoordinaten). u ist hier der Polarwinkel (meist
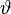 oder
oder 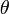 ) und v der Azimutwinkel (meist
) und v der Azimutwinkel (meist 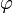 oder
oder 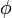 bezeichnet).
bezeichnet).- Beispiel 2: Ist
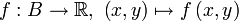 eine Funktion und die Fläche in der Form z = f(x,y) angegeben so sind x und y die beiden Parameter; die Parametrisierung der Fläche sieht also wie folgt aus:
eine Funktion und die Fläche in der Form z = f(x,y) angegeben so sind x und y die beiden Parameter; die Parametrisierung der Fläche sieht also wie folgt aus:
Auf der Fläche
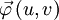 bilden die Kurvenscharen u = const bzw. v = const die Koordinatenlinien. Diese überziehen die Fläche mit einem Koordinatennetz, wobei durch jeden Punkt zwei Koordinatenlinien verlaufen. Somit hat jeder Punkt auf der Fläche eindeutige Koordinaten
bilden die Kurvenscharen u = const bzw. v = const die Koordinatenlinien. Diese überziehen die Fläche mit einem Koordinatennetz, wobei durch jeden Punkt zwei Koordinatenlinien verlaufen. Somit hat jeder Punkt auf der Fläche eindeutige Koordinaten 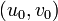 .
.Oberflächenelement
Wenn im eindimensionalen Fall das dx die Breite eines unendlich kleinen Intervalls darstellt, so liegt es nahe, es im zweidimensionalen Fall durch die Fläche eines unendlich kleinen Flächenstückes dσ zu ersetzen. Durch die im vorhergehenden Abschnitt beschriebene Parametrisierung kann man an jeden Punkt der Oberfläche zwei Tangenten legen: Einmal die Tangente, die entsteht, wenn man v konstant lässt und u minimal variiert, und einmal mit vertauschten Variablen. Das heißt also zwei Tangenten an die beiden Koordinatenlinien im betrachteten Punkt
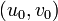 . Diese Tangenten lassen sich durch zwei infinitesimale Tangentenvektoren ausdrücken (sei
. Diese Tangenten lassen sich durch zwei infinitesimale Tangentenvektoren ausdrücken (sei 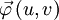 die parametrische Form der Fläche):
die parametrische Form der Fläche):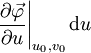 und
und 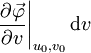
Im Folgenden wird die kompakte Schreibweise für die partiellen Ableitungen verwendet:
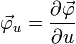 und
und 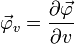
Sind diese Tangenten in keinem Punkt der Fläche parallel, so spricht man von einer regulären Parametrisierung. Das Kreuzprodukt der Tangentenvektoren ist dann ein Vektor, dessen Länge ungleich Null ist.
Die beiden Tangentenvektoren liegen in der Tangentialebene der Fläche am betrachteten Punkt. Der Flächeninhalt des von beiden Tangentenvektoren aufgespannten Parallelogramms entspricht nun gerade dem Betrag ihres Kreuzproduktes.
Ist nun
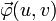 eine reguläre Parametrisierung der Oberfläche, so definiert man:
eine reguläre Parametrisierung der Oberfläche, so definiert man:- Skalares Oberflächenelement
- Vektorielles Oberflächenelement
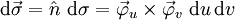 mit dem Einheitsnormalenvektor des Flächenelements
mit dem Einheitsnormalenvektor des Flächenelements 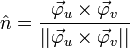
Gemäß den Eigenschaften des Kreuzprodukts steht das vektorielle Oberflächenelement senkrecht auf der Fläche, sein Betrag entspricht gerade der Größe des infinitesimalen Flächenstücks.
In der oben vorgestellten Form ist das vektorielle Oberflächenelement nicht wohldefiniert, da seine Richtung davon abhängt ob man
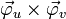 oder
oder 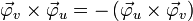 berechnet. Die beiden Möglichkeiten sind antiparallel zueinander. Betrachtet man geschlossene Oberflächen, vereinbart man meist, dass das nach außen weisende vektorielle Oberflächenelement zu verwenden ist.
berechnet. Die beiden Möglichkeiten sind antiparallel zueinander. Betrachtet man geschlossene Oberflächen, vereinbart man meist, dass das nach außen weisende vektorielle Oberflächenelement zu verwenden ist.- Beispiel 1: Die Oberfläche der Kugel mit Radius R kann, wie oben gezeigt, durch den Polarwinkel u und den Azimutwinkel v parametrisiert werden. Das Flächenelement ergibt sich aus folgender Rechnung:
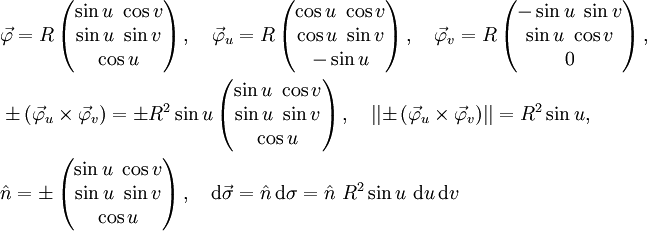
- Beim Normalenvektor sind zwei Lösungen möglich (
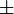 ), abhängig von der Reihenfolge von
), abhängig von der Reihenfolge von 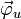 und
und 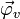 im Kreuzprodukt. Typischerweise wählt man hier die positive Lösung, bei der
im Kreuzprodukt. Typischerweise wählt man hier die positive Lösung, bei der 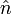 von der konvexen Kugeloberfläche weg zeigt.
von der konvexen Kugeloberfläche weg zeigt.
- Beispiel 2: Ist die Fläche in der Form z = f(x,y) angegeben, so drückt man das Flächenelement durch die Differentiale der Koordinaten x, y aus. Dies lässt sich in der allgemeinen Form angeben:
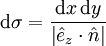 mit
mit 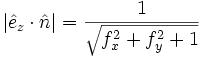
- Dabei ist
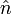 der Normaleneinheitsvektor,
der Normaleneinheitsvektor, 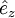 der Einheitsvektor in z-Richtung, fx die Ableitung von f(x,y) nach x. Dies lässt sich mit den von oben bekannten elementaren Formeln zeigen:
der Einheitsvektor in z-Richtung, fx die Ableitung von f(x,y) nach x. Dies lässt sich mit den von oben bekannten elementaren Formeln zeigen: 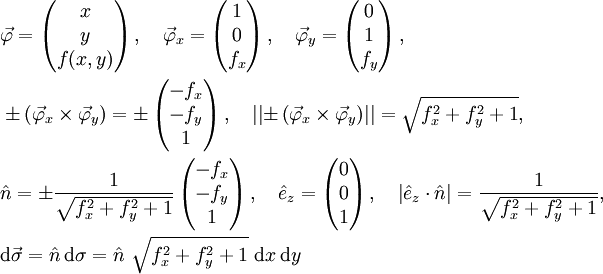
Die Integrale
Mit den Parametrisierungen und den Oberflächenelementen kann man nun die Oberflächenintegrale definieren. Diese mehrdimensionalen Integrale sind Lebesgue-Integrale, können aber in den meisten Anwendungsfällen als mehrfache Riemann-Integrale berechnet werden.
Das skalare Oberflächenintegral
Das skalare Oberflächenintegral einer skalaren Funktion
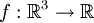 über eine Oberfläche
über eine Oberfläche 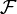 mit regulärer Parametrisierung
mit regulärer Parametrisierung 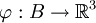 mit
mit 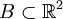 ist definiert als
ist definiert alsSetzt man beispielsweise
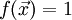 , so ist das skalare Oberflächenintegral einfach der Flächeninhalt der Oberfläche.
, so ist das skalare Oberflächenintegral einfach der Flächeninhalt der Oberfläche.Das vektorielle Oberflächenintegral
Das vektorielle Oberflächenintegral einer vektorwertigen Funktion
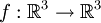 über eine Oberfläche
über eine Oberfläche 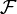 mit regulärer Parametrisierung
mit regulärer Parametrisierung 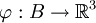 mit
mit 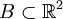 ist definiert als
ist definiert als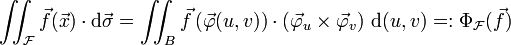 .
.
Eine anschauliche Vorstellung dieses Integrals geschieht über den Fluss Φ eines Vektorfeldes
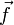 durch die Fläche
durch die Fläche 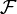 : Die Größe
: Die Größe 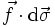 gibt an, welchen Beitrag zum Gesamtfluss
gibt an, welchen Beitrag zum Gesamtfluss 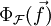 der infinitesimal-kleine Oberflächen-Vektor
der infinitesimal-kleine Oberflächen-Vektor 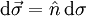 liefert.
liefert.
Wikimedia Foundation.