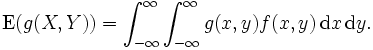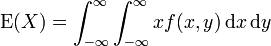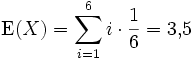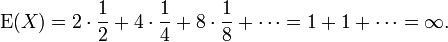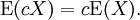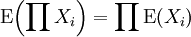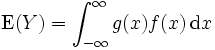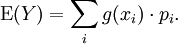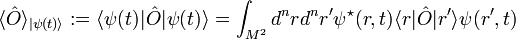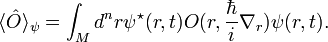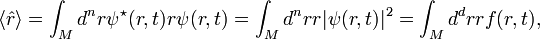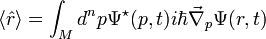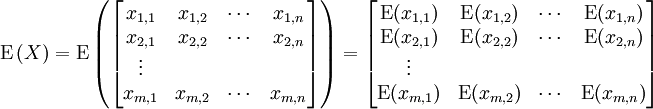- Grundgesamtheitsmittelwert
-
Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Begriff der Stochastik. Der Erwartungswert (
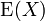 oder μ) einer Zufallsvariablen (X) ist jener Wert, der sich (in der Regel) bei oftmaligem Wiederholen des zugrunde liegenden Experiments als Mittelwert der Ergebnisse ergibt. Er bestimmt die Lokalisation (Lage) einer Verteilung und ist vergleichbar mit dem empirischen arithmetischen Mittel einer Häufigkeitsverteilung in der deskriptiven Statistik. Das Gesetz der großen Zahlen sichert in vielen Fällen zu, dass der Stichprobenmittelwert bei wachsender Stichprobengröße gegen den Erwartungswert konvergiert.
oder μ) einer Zufallsvariablen (X) ist jener Wert, der sich (in der Regel) bei oftmaligem Wiederholen des zugrunde liegenden Experiments als Mittelwert der Ergebnisse ergibt. Er bestimmt die Lokalisation (Lage) einer Verteilung und ist vergleichbar mit dem empirischen arithmetischen Mittel einer Häufigkeitsverteilung in der deskriptiven Statistik. Das Gesetz der großen Zahlen sichert in vielen Fällen zu, dass der Stichprobenmittelwert bei wachsender Stichprobengröße gegen den Erwartungswert konvergiert.Ein Erwartungswert muss kein mögliches Ergebnis des zugrunde liegenden Zufallsexperiments sein. Insbesondere kann der Erwartungswert die Werte
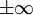 annehmen.
annehmen.Inhaltsverzeichnis
Definitionen
Allgemein wird der Erwartungswert als das Integral bezüglich des Wahrscheinlichkeitsmaßes definiert: Ist X eine P-integrierbare oder quasiintegrierbare Zufallsvariable von einem Wahrscheinlichkeitsraum (Ω,Σ,P) nach
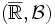 , wobei
, wobei  die Borelsche σ-Algebra über
die Borelsche σ-Algebra über 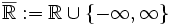 ist, so definiert man
ist, so definiert man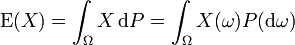 .
.
Ist eine Zufallsvariable diskret oder besitzt sie eine Dichte, so existieren einfachere Formeln für den Erwartungswert, die im Folgenden aufgeführt sind.
Erwartungswert einer diskreten Zufallsvariablen
Im diskreten Fall errechnet sich der Erwartungswert als die Summe der Produkte aus den Wahrscheinlichkeiten jedes möglichen Ergebnisses des Experiments und den „Werten“ dieser Ergebnisse.
Ist X eine diskrete Zufallsvariable, die die Werte x1, x2, ... mit den jeweiligen Wahrscheinlichkeiten p1, p2, ... annimmt, errechnet sich der Erwartungswert
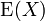 zu:
zu:Sonderfall: abzählbar unendlich viele Werte einer diskreten Zufallsvariablen
Nimmt die Zufallsvariable X abzählbar unendlich viele Werte an, dann liegt eine unendliche Reihe vor. In diesem Fall existiert der Erwartungswert
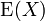 nur, wenn die Konvergenzbedingung
nur, wenn die Konvergenzbedingung erfüllt ist, d. h. die Summe für den Erwartungswert absolut konvergent ist.
erfüllt ist, d. h. die Summe für den Erwartungswert absolut konvergent ist.
Erwartungswert einer stetigen Zufallsvariablen mit Dichtefunktion
Hat eine Zufallsvariable X eine Wahrscheinlichkeitsdichtefunktion f, so berechnet sich der Erwartungswert zu
Der Erwartungswert existiert nur, wenn das Integral für den Erwartungswert absolut konvergent ist, d. h. wenn das Integral
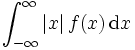 konvergiert.
konvergiert.Beispiel
Gegeben ist die Zufallsvariable X mit der Dichtefunktion
Der Erwartungswert berechnet sich als
Erwartungswert von zwei Zufallsvariablen mit gemeinsamer Dichtefunktion
Haben eine Zufallsvariable X und eine Zufallsvariable Y eine gemeinsame Wahrscheinlichkeitsdichtefunktion f(x,y), so berechnet sich der Erwartungswert einer Funktion g(X,Y) von X und Y zu
Der Erwartungswert existiert nur, wenn das Integral
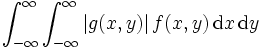 konvergiert.
konvergiert.Insbesondere ist:
Aus der Randdichte errechnet sich der Erwartungswert wie bei univariaten Verteilungen:
Beispiele
Würfeln
Das Experiment sei ein Würfelwurf. Als Zufallsvariable X betrachten wir die gewürfelte Augenzahl, wobei jede der Zahlen 1 bis 6 mit einer Wahrscheinlichkeit von jeweils 1/6 gewürfelt wird.
Wenn man beispielsweise 1000 Mal würfelt, d. h. das Zufallsexperiment 1000 mal wiederholt, die geworfenen Augenzahlen zusammenzählt und durch 1000 dividiert, ergibt sich mit hoher Wahrscheinlichkeit ein Wert in der Nähe von 3,5. Es ist jedoch unmöglich, diesen Wert mit einem einzigen Würfelwurf zu erzielen.
St. Petersburger Spiel
Das sogenannte St. Petersburger Spiel ist ein Spiel, dessen zufälliger Gewinn X einen unendlichen Erwartungswert hat. Man werfe eine Münze, zeigt sie Kopf, erhält man 2 Euro, zeigt sie Zahl, darf man nochmals werfen. Wirft man nun Kopf, erhält man 4 Euro, wirft man wieder Zahl, so darf man ein drittes Mal werfen usw. Der Erwartungswert des Gewinnes X ist unendlich:
Rechenregeln
Der Erwartungswert ist linear, da das Integral ein linearer Operator ist. Daraus ergeben sich die folgenden zwei sehr nützlichen Regeln:
Erwartungswert der Summen von n Zufallsvariablen
Der Erwartungswert der Summe von n Zufallsvariablen (Xi) lässt sich berechnen als die Summe der einzelnen Erwartungswerte:
Lineare Transformation
Für die Lineare Transformation
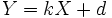 gilt
gilt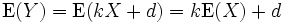 ,
,
insbesondere auch
Erwartungswert des Produkts von n Zufallsvariablen
Wenn die Zufallsvariablen Xi stochastisch voneinander unabhängig sind, gilt:
Wahrscheinlichkeiten als Erwartungswerte
Wahrscheinlichkeiten von Ereignissen lassen sich auch über den Erwartungswert ausdrücken. Für jedes Ereignis A gilt
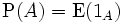 ,
,
wobei 1A die Indikatorfunktion von A ist.
Dieser Zusammenhang ist oft nützlich, etwa zum Beweis der Tschebyschow-Ungleichung.
Erwartungswerte von Funktionen von Zufallsvariablen
Wenn Y = g(X) wieder eine Zufallsvariable ist, so kann man den Erwartungswert von Y mittels
berechnen. Auch in diesem Fall existiert der Erwartungswert nur, wenn
konvergiert. Bei einer diskreten Zufallsvariable verwendet man eine Summe:
Ist die Summe nicht endlich, dann muss die Reihe absolut konvergieren, damit der Erwartungswert existiert.
Quantenmechanischer Erwartungswert
Ist
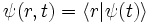 die Wellenfunktion eines Teilchens in einem bestimmten Zustand
die Wellenfunktion eines Teilchens in einem bestimmten Zustand  und ist
und ist 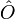 ein Operator, so ist
ein Operator, so istder quantenmechanische Erwartungswert von
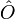 im Zustand
im Zustand  . M ist hierbei der Ortsraum, in dem sich das Teilchen bewegt, n ist die Dimension von M, und ein hochgestellter Stern steht für komplexe Konjugation.
. M ist hierbei der Ortsraum, in dem sich das Teilchen bewegt, n ist die Dimension von M, und ein hochgestellter Stern steht für komplexe Konjugation.Lässt sich
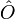 als formale Potenzreihe
als formale Potenzreihe 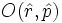 schreiben (und das ist oft so), so verwendet man die Formel
schreiben (und das ist oft so), so verwendet man die FormelDer Index an der Erwartungswertsklammer wird nicht nur wie hier abgekürzt, sondern manchmal auch ganz weggelassen.
Beispiel
Der Erwartungswert des Aufenthaltsorts in Ortsdarstellung ist
Der Erwartungswert des Aufenthaltsorts in Impulsdarstellung ist
wobei wir die Wahrscheinlichkeitsdichtefunktion der Quantenmechanik im Ortsraum identifiziert haben. In der Physik schreibt man ρ (rho) statt f.
Erwartungswert von Matrizen
Ist X eine
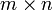 Matrix, dann ist der Erwartungswert der Matrix definiert als:
Matrix, dann ist der Erwartungswert der Matrix definiert als:Siehe auch
- Varianz
- Parameter (Statistik)
- Moment
- Momenterzeugende Funktion
- Charakteristische Funktion (Stochastik)
- Bedingter Erwartungswert
Literatur
- Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck & Ruprecht, Göttingen 1974, ISBN 3-525-03114-9
Weblinks
- Erwartungswert Zufallsvariable, Wahrscheinlichkeitsverteilungen, Erwartungswert
Wikimedia Foundation.

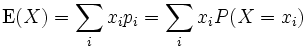

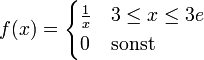
![\begin{align}
\operatorname E(X)&= \int_{-\infty}^\infty x f(x)\,\mathrm{d}x\\
&= \int_{-\infty}^3 x \cdot 0\,\mathrm{d}x + \int_3^{3e} x \cdot \frac 1x\,\mathrm{d}x + \int_{3e}^\infty x \cdot 0 \,\mathrm{d}x\\
&= 0 + \int_3^{3e} 1\,\mathrm{d}x + 0\\
&= [x]^{3e}_3\\
&= 3e-3.
\end{align}](/pictures/dewiki/56/8749d8a3db9338abd7568ffc90046a73.png)