Kleinerzeichen

Satzzeichen
-, –, —, ―
. ,  , ,  ; ,  : ,  … ,  ·
¿, ?, !, ¡, ‽, ؟
„…“, »…« …,  ’
/, \
(…), […], {…}, 〈…〉
␠
Sonstige Zeichen
•  …
@, &
|, ¦
°, ′, ″, ‴
*, ⁂, †, ‡
#, №, ª, º
§, ¶
©, ℗, ®, ™, ℠
_
~, ˜
Rechenzeichen
+, −, ×, ∙, :, ∕, ÷, ±, ∓
=, ≈, ≠ …, ~, ∝ …, <, > …
√, ∫
%, ‰

Verhältniszeichen sind die in der mathematischen Notation üblichen Zeichen für die Darstellung der Größenverhältnisse zweier Zahlen bzw. Terme.

Die wichtigsten Verhältniszeichen sind das Gleichheitszeichen (=) sowie die Größer-als-Zeichen (>) und Kleiner-als-Zeichen (<). Die beiden letztgenannten Zeichen werden genutzt, um Ungleichungen auszudrücken.

Verhältniszeichen können vielfältig kombiniert werden, unter anderem auch mit einem senkrechten Strich (|) zur Negation oder einer Tilde für die Äquivalenz. Viele der Kombinationen fallen in den meisten Anwendungen mit der Bedeutung anderer Zeichen zusammen.

Formelsatz

Die Zeichen > und < wurden vom englischen Mathematiker Thomas Harriot eingeführt.

Je nach Tradition des Formelsatzes werden manchmal geringfügig abweichende Verhältniszeichen verwendet. Die folgende Zuordnung ist nicht restriktiv, die entsprechenden Formen können auch in den ihnen nicht zugeordneten Traditionen auftauchen. Die Polen, Russland und der ehemaligen UdSSR zugeordnete Form tritt beispielsweise auch in IUPAC-Veröffentlichungen auf, während die anglo-amerikanische Form überall auf der Welt verwendet wird.

Form	Herkunft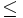
$\!\!\leq$	Anglo-amerikanischer Raum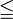
$\leqq$	Deutschland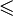
$\leqslant$	Polen, Russland und ehemalige Sowjetunion

Das gilt für die anderen Zeichen entsprechend.

Kleiner-als-Zeichen

Das Kleinerzeichen (<) kennzeichnet eine zweistellige Relation, deren semantische Belegung von der verwendeten Algebra abhängt. Implizit wird angenommen, dass die Relation zu 'wahr' ausgewertet wird.

Im täglichen Sprachgebrauch der natürlichen Zahlen bezeichnet man damit die Relation eines echt kleineren (nicht gleichgroßen!) Wertes gegenüber einem echt größeren Wert. In Präfixnotation bedeutet das: < (a, b) wird zu 'wahr' ausgewertet, also a ist echt kleiner als b.

Die gebräuchlichere Form ist die Infixnotation a < b, wenn a echt kleiner ist als b.

Das Schriftzeichen hat den Unicode-Wert U+003C, gehört also zum ASCII-Satz.

Merksätze

• Zur Vermeidung von Verwechslungen zwischen den Zeichen "Größer-als" und "Kleiner-als" ist - gerade für Schulkinder - ein Vergleich mit einem Krokodil hilfreich, das stets nach dem größeren "Bissen" schnappt: "Das Krokodil, das Krokodil, stets das Meiste fressen will".
• Alternativ kann das Zeichen "Kleiner-als" durch einen senkrechten Strich zu einem K und das "Größer-als" durch einen Halbkreis zu einem G stilisiert werden.

Beispiel

Der Wert der natürlichen Zahl 3 ist echt kleiner (hat eine geringere Ordnung), als der Wert der natürlichen Zahl 4. Die Ordnung gibt der Zahlenstrahl der natürlichen Zahlen vor.

Man schreibt:

3 < 4

Ebenso gilt für reelle Zahlen:

3,14 < 3,15

Liste der Verhältniszeichen

Mathematische Verhältniszeichen

Zeichen		Unicode		Bedeutung		Zeichen		Unicode		Bedeutung
=	≠	U+003D	U+2260	gleich/ungleich		≈		U+2248		fast gleich
<	>	U+003C	U+003E	kleiner/größer als		≺	≻	U+227A	U+227B	vorangehend/nachfolgend
≤	≥	U+2264	U+2265	kleiner/größer oder gleich		≼	≽	U+227C	U+227D	vorangehend/nachfolgend oder gleich
≮	≯	U+226E	U+226F	nicht kleiner/größer als		⊀	⊁	U+2280	U+2281	nicht vorangehend/nachfolgen
≰	≱	U+2270	U+2271	weder kleiner/größer als noch gleich		⋠	⋡	U+22E0	U+22E1	weder vorangehend/nachfolgend noch gleich
≲	≳	U+2272	U+2273	kleiner/größer als oder äquivalent		≾	≿	U+227E	U+227F	vorangehend/nachfolgend oder äquivalent
⋜	⋝	U+22DC	U+22DD	gleich oder kleiner/größer als		⋞	⋟	U+22DE	U+22DF	gleich oder vorangehend/nachfolgend
⋦	⋧	U+22E6	U+22E7	kleiner/größer als, aber nicht äquivalent		⋨	⋩	U+22E8	U+22E9	vorangehend/nachfolgend, aber nicht äquivalent
≴	≵	U+2274	U+2275	weder kleiner/größer als noch äquivalent
≦	≧	U+2266	U+2267	kleiner/größer als über gleich zu
≨	≩	U+2268	U+2269	kleiner/größer als, aber nicht gleich
≪	≫	U+226A	U+226B	viel kleiner/größer als
⋘	⋙	U+22D8	U+22D9	sehr viel kleiner/größer als
≶	≷	U+2276	U+2277	kleiner/größer oder größer/kleiner als
≸	≹	U+2278	U+2279	weder kleiner/größer noch größer/kleiner als
⋚	⋛	U+22DA	U+22DB	kleiner/größer als, gleich oder größer/kleiner als
⋖	⋗	U+22D6	U+22D7	kleiner/größer als mit Punkt		⊰	⊱	U+22B0	U+22B1	vorangehend/nachfolgend in Relation

Siehe auch

• Vergleichsoperator