- Krummliniges Koordinatensystem
-
Es gibt zwei bekannte und gebräuchliche Darstellungen von Vektoren in krummlinigen Koordinaten, die beide zu den orthogonale Koordinatensystemen zählen:
- ebene Polarkoordinaten (2D) bzw. deren 3-dimensionale Entsprechung, die Zylinderkoordinaten
- Kugelkoordinaten, auch sphärische Koordinaten genannt (3D)
Inhaltsverzeichnis
Transformation von kartesischen Koordinaten
Die kartesischen Koordinaten xi lassen sich als Funktionen neuer Koordinaten ui schreiben:
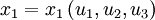 ,
, 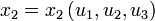 ,
, 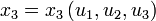
Dies stellt ein Gleichungssystem dar, das nach den ui auflösbar ist, wenn die Funktionaldeterminante ungleich null ist:
Koordinatenlinien erhält man indem jeweils zwei Koordinaten festgehalten und die dritte variiert wird. In jedem Punkt des 3-dimensionalen Raumes dürfen sich nur 3 Koordinatenlinien schneiden, da sonst dieser Punkt keine eindeutigen Koordinaten besitzt (Funktionaldeterminante gleich null). Als Beispiel für diese Uneindeutigkeit zählt der Ursprung bei den Kugelkoordinaten, bei dem sich alle Radial-Koordinatenlinien schneiden; somit sind die Koordinaten des Ursprungs nicht eindeutig (r = 0, aber θ und φ beliebig). Koordinatenflächen erhält man indem jeweils eine Koordinate festgehalten und die beiden anderen variiert werden.
Basisvektoren
Die Tangenteneinheitsvektoren an die Koordinatenlinien erhält man aus:
Diese Einheitsvektoren haben im Allgemeinen eine vom Ort abhängige Richtung
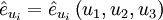 .
.Im Folgenden verwendete Definition:
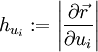 somit
somit 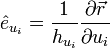
Spezialfall: Orthogonale Koordinaten
Schneiden sich an jedem Raumpunkt die 3 Koordinatenlinien paarweise senkrecht, so spricht man von einem orthogonalen Koordinatensystem. Die Einheitsvektoren
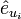 bilden also eine orthonormale Basis des
bilden also eine orthonormale Basis des 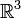 :
: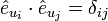 , i,j = 1,2,3 (δ:Kronecker-Delta)
, i,j = 1,2,3 (δ:Kronecker-Delta)
Bilden die orthonormalen Basisvektoren eine rechtshändige Basis (positive Orientierung), gelten folgende Beziehungen:
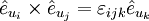 , i,j,k = 1,2,3 (
, i,j,k = 1,2,3 ( : Levi-Civita-Symbol)
: Levi-Civita-Symbol)
Vektoren als Linearkombination der Basisvektoren
Mit der neuen Basis lassen sich nun alle Vektoren
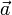 durch die Basisvektoren
durch die Basisvektoren 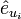 ausdrücken:
ausdrücken:Dabei ist
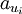 die Vektorkomponente, die in Richtung der ui-Koordinatenlinie zeigt. Diese lässt sich für eine orthonormale Basis einfach durch folgende Projektion bestimmen:
die Vektorkomponente, die in Richtung der ui-Koordinatenlinie zeigt. Diese lässt sich für eine orthonormale Basis einfach durch folgende Projektion bestimmen:Bei nicht orthogonalen Koordinatensystemen (schiefwinklig) bestimmt man die Vektorkomponente
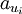 durch Projektion auf den dualen Basisvektor
durch Projektion auf den dualen Basisvektor 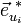 . Das Skalarprodukt aus Basisvektoren
. Das Skalarprodukt aus Basisvektoren 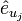 (kontravariante Vektoren) und dualen Basisvektoren
(kontravariante Vektoren) und dualen Basisvektoren 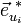 (kovariante Vektoren) ergibt:
(kovariante Vektoren) ergibt:  .
.Ableitungen der Basisvektoren
Die Ableitungen von Vektoren, die in krummlinigen Koordinaten dargestellt werden, weisen gegenüber den kartesischen folgende Besonderheit auf. Da die Koordinatenlinien im Allgemeinen keine Geraden sind und daher die Basisvektoren eine vom Ort abhängige Richtung haben, müssen die Basisvektoren auch differenziert werden (Anwenden der Produktregel):
Integrationselemente
Ein Wegelement oder Linienelement
 kann als totales Differential des Ortsvektors dargestellt werden.
kann als totales Differential des Ortsvektors dargestellt werden.Die Differentiale in Richtung der ui-Koordinatenlinien können identifiziert werden:
Damit können nun Bogen-, Flächen- und Volumenelement bestimmt werden.
Kurvenelement
Kurvenelement bzw. Bogenelement:
für orthogonale Koordinaten
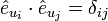 gilt:
gilt:Flächenelement
Flächenelement einer Koordinatenfläche, sei ohne Beschränkung der Allgemeinheit u1 = const:
für orthogonale Koordinaten gilt:
Volumenelement
hier lässt sich der Betrag der Funktionaldeterminante identifizieren:
für orthogonale Koordinaten gilt:
Differentialoperatoren
Es werden die Differentialoperatoren Gradient, Divergenz, Rotation und Laplace für orthogonale Koordinatensysteme angegeben:
Literatur
Günter Bärwolff: Höhere Mathematik für Naturwissenschaftler und Ingenieure. Spektrum Akademischer Verlag, ISBN 978-3827416889
Weblinks
Siehe auch
Wikimedia Foundation.

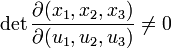

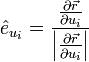
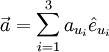


![\frac{\partial \vec{a}}{\partial u_{i}}=\sum\limits_{i=1}^{3}{\frac{\partial \left( a_{u_{i}}\hat{e}_{u_{i}} \right)}{\partial u_{i}}}=\sum\limits_{i=1}^{3}{\left[ \frac{\partial a_{u_{i}}}{\partial u_{i}}\hat{e}_{u_{i}}+a_{u_{i}}\frac{\partial \hat{e}_{u_{i}}}{\partial u_{i}} \right]}](/pictures/dewiki/57/9061ca029baf67c080fbd2a9ea1cf206.png)
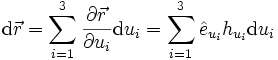
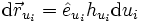




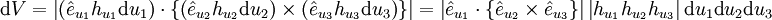

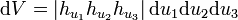
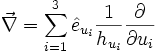
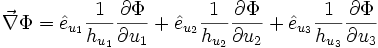
![\vec{\nabla} \cdot \vec{a}=\frac{1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}\left[ \frac{\partial }{\partial u_{1}}\left( h_{u_{2}}h_{u_{3}}a_{u_{1}} \right)+\frac{\partial }{\partial u_{2}}\left( h_{u_{1}}h_{u_{3}}a_{u_{2}} \right)+\frac{\partial }{\partial u_{3}}\left( h_{u_{1}}h_{u_{2}}a_{u_{3}} \right) \right]](/pictures/dewiki/50/2abe8218d0807124eced7620f7367af4.png)

![\Delta \Phi =\frac{1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}\left[ \frac{\partial }{\partial u_{1}}\left( \frac{h_{u_{2}}h_{u_{3}}}{h_{u_{1}}}\frac{\partial \Phi }{\partial u_{1}} \right)+\frac{\partial }{\partial u_{2}}\left( \frac{h_{u_{1}}h_{u_{3}}}{h_{u_{2}}}\frac{\partial \Phi }{\partial u_{2}} \right)+\frac{\partial }{\partial u_{3}}\left( \frac{h_{u_{1}}h_{u_{2}}}{h_{u_{3}}}\frac{\partial \Phi }{\partial u_{3}} \right) \right]](/pictures/dewiki/100/d5f12bb902289f997a0e3ded0fdd6d80.png)