Nullabbildung

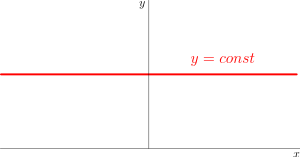
In der Mathematik ist eine konstante Funktion eine Funktion, die für alle Argumente stets denselben, also konstanten Funktionswert annimmt.

Definition und Charakterisierung

Sei 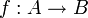$f:A \to B$ eine Funktion zwischen zwei nichtleeren Mengen. Dann ist f konstant, wenn für alle 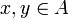$x,y \in A$ gilt: f(x) = f(y).

Äquivalent zu dieser Definition ist die Aussage, dass die Bildmenge von f aus genau einem Element besteht.

Insbesondere in der Kategorientheorie werden konstante Funktionen mittels Hintereinanderausführung charakterisiert:

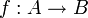$f:A \to B$ ist genau dann konstant, wenn für alle Funktionen 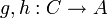$g,h:C \to A$ gilt: $f \circ g = f \circ h$.

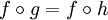Auf diese Weise werden konstante Morphismen sauber definiert. Gebräuchlich ist weiterhin: Ist für jede Funktion 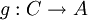$g: C \to A$ die Verknüpfung 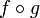$f \circ g$ konstant, dann ist auch f konstant.

Eigenschaften, bekannte Funktionen

Konstante Funktion

Im Fall einer konstanten Funktion von den reellen Zahlen in die reellen Zahlen ist ihr Graph eine zur x-Achse parallele („waagerechte“) Gerade.

• Ist der Wert der Funktion die Zahl Null, so handelt es sich um den Spezialfall der Nullfunktion. Sowohl in der reellen als auch der komplexen Differentialrechnung ist die Ableitung einer konstanten Funktion die Nullfunktion. Definiert man eine Vektorraum-Struktur auf einer Menge von Funktionen, so entspricht die Nullfunktion stets dem Nullvektor.

• Ist der Funktionswert Eins, spricht man häufig von der Einsfunktion. Sie ist die Ableitung der Identität.

Der Begriff „Einsfunktion“ wird jedoch noch ein einem anderen Kontext verwendet. Mittels Hintereinanderausführung kann eine Gruppenstruktur auf einer Menge von Funktionen definiert werden. Das neutrale Element dieser Gruppe wird auch oft mit „Einsfunktion“ bezeichnet, ist aber keine konstante Funktion, sondern die identische Abbildung.

• Polynome nullten Grades sind konstante Funktionen. Zwischen Vektorräumen ist eine konstante Funktion genau dann eine lineare Abbildung, wenn es sich um die Nullfunktion handelt.

Die Konstanz einer Funktion ist nicht immer augenfällig: Betrachtet man eine beliebig vorgegebene Funktion, so kann sie konstant sein, obwohl ihr Funktionsterm scheinbar vom Argument abhängt. Ein Beispiel ist die Funktion 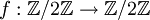$f:\Z/2\Z \to \Z/2\Z$, also auf dem Restklassenring modulo 2, mittels f(x) = x² − x. Diese Funktion ist konstant 0 (da 0² − 0 = 0 und 1² − 1 = 0).

Weitere Zusammenhänge, Verallgemeinerungen

• Der Satz von Liouville besagt, dass eine beschränkte, ganze Funktion konstant ist. Daraus folgt auch, dass eine elliptische Funktion ohne Polstelle konstant ist.
• Eine Verallgemeinerung von konstanten Funktionen sind lokal konstante Funktionen, bei denen für jedes Argument x eine Umgebung um x existiert, auf der sie konstant sind. Damit lassen sich beispielsweise folgende Sätze formulieren:
  • Sei Y eine Menge, die mehr als ein Element enthält. Ein topologischer Raum X ist zusammenhängend, wenn jede lokal konstante Funktion 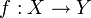$f:X \to Y$ konstant ist.
  • Sei 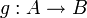$g:A \to B$ eine stetige Funktion zwischen zwei topologischen Räumen. Ist A zusammenhängend und B diskret, so ist g konstant.
• Lässt man auch leere Mengen zu, so hängt es von der Betrachtungsweise ab, ob die Funktion 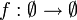$f:\emptyset\to\emptyset$ mit leerer Definitions- und Zielmenge als konstant angesehen wird oder nicht, da die Äquivalenz in obiger Definition nicht mehr gilt.