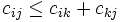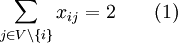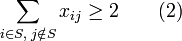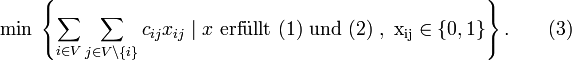Traveling-Salesperson-Problem

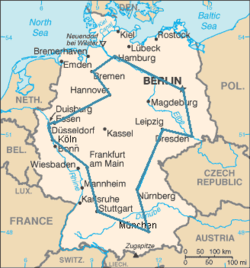
Optimaler Reiseweg eines Handlungsreisenden durch die 15 größten Städte Deutschlands. Die angegebene Route ist die kürzeste von 43.589.145.600 möglichen.

Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein kombinatorisches Optimierungsproblem des Operations Research und der theoretischen Informatik. Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die gesamte Reisestrecke des Handlungsreisenden nach der Rückkehr zum Ausgangsort möglichst kurz ist.

Seit seiner ersten Erwähnung als mathematisches Problem im Jahre 1930 haben sich viele Forscher damit befasst und neue Optimierungsverfahren daran entwickelt und erprobt, die momentan auch für andere Optimierungsprobleme eingesetzt werden. Heute steht eine Vielzahl von heuristischen und exakten Methoden zur Verfügung, mit denen auch schwierige Fälle mit mehreren tausend Städten optimal gelöst wurden.

Das Problem des Handlungsreisenden tritt schon in seiner Reinform in vielen praktischen Anwendungen auf, beispielsweise in der Tourenplanung, in der Logistik oder im Design von Mikrochips. Noch häufiger tritt es allerdings als Unterproblem auf, wie z. B. bei der Verteilung von Waren, bei der Planung von Touren eines Kunden- oder Pannendienstes oder bei der Genom-Sequenzierung. Dabei sind die Begriffe „Stadt“ und „Entfernung“ nicht wörtlich zu nehmen, vielmehr repräsentieren die Städte beispielsweise zu besuchende Kunden, Bohrlöcher oder DNA-Teilstränge, während Entfernung für Reisezeit, Kosten oder den Grad der Übereinstimmung zweier DNA-Stränge steht. In vielen praktischen Anwendungen müssen zudem Zusatzbedingungen wie Zeitfenster oder eingeschränkte Ressourcen beachtet werden, was die Lösung des Problems erheblich erschwert.

Komplexitätstheoretisch gehört das TSP zur Klasse der NP-äquivalenten Probleme. Es wird daher sehr stark angenommen, dass die Worst-case-Laufzeit jedes deterministischen Algorithmus, der für dieses Problem stets optimale Lösungen liefert, im besten Fall exponentiell von der Anzahl der Städte abhängt. Schon für wenige Städte kann die benötigte Laufzeit eines solchen Algorithmus also unpraktikabel viel Zeit beanspruchen.

Geschichte

Wann das Problem des Handlungsreisenden das erste Mal wissenschaftlich untersucht wurde, ist unklar. Aus dem Jahre 1832 ist ein Handbuch für Handlungsreisende bekannt (Titel: „Der Handlungsreisende – wie er sein soll und was er zu thun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiß zu sein – von einem alten Commis-Voyageur“), in dem das Problem erwähnt, aber nicht mathematisch behandelt wird. Stattdessen werden Beispieltouren für einige Regionen Deutschlands und der Schweiz vorgeschlagen.

William Rowan Hamilton

Als früher Vorläufer des Problems kann das Icosian Game von William Rowan Hamilton aus dem 19. Jahrhundert angesehen werden, bei dem es darum ging, in einem Graphen Touren zwischen 20 Knoten zu finden. Die erste explizite Erwähnung als mathematisches Optimierungsproblem scheint jedoch auf Karl Menger zurückführbar zu sein, der dieses 1930 in einem mathematischen Kolloquium in Wien folgendermaßen formulierte:

„Wir bezeichnen als Botenproblem (weil diese Frage in der Praxis von jedem Postboten, übrigens auch von vielen Reisenden zu lösen ist) die Aufgabe, für endlich viele Punkte, deren paarweise Abstände bekannt sind, den kürzesten die Punkte verbindenden Weg zu finden.“

Schon bald darauf wurde die heute übliche Bezeichnung Traveling Salesman Problem durch Hassler Whitney von der Princeton University eingeführt.

Neben der einfachen Definition und Verständlichkeit der Aufgabenstellung zeichnet sich das Problem des Handlungsreisenden dadurch aus, dass die Bestimmung guter Lösungen vergleichsweise leicht ist, während das Finden einer beweisbar optimalen Lösung sehr schwierig ist. Aufgrund dieser Eigenschaften ist die Beschäftigung mit dem Problem seit der zweiten Hälfte des 20. Jahrhunderts nicht so sehr durch direkte Anwendungen motiviert, es dient vielmehr als eine Art Spielwiese zur Entwicklung neuer Optimierungsverfahren.

Viele heutige Standardmethoden der ganzzahligen linearen Optimierung, wie Schnittebenenverfahren, Branch-and-Cut und verschiedene heuristische Ansätze, sind am Beispiel des TSP entwickelt und getestet worden.

In den 1950er und 1960er Jahren gewann das Problem des Handlungsreisenden sowohl in Europa als auch in den USA zunehmend an wissenschaftlicher Popularität. Besonders herausragende Beiträge stammen von George Dantzig, Delbert Ray Fulkerson und Selmer M. Johnson, die 1954 am Institut der RAND Corporation in Santa Monica sowohl die erste Formulierung des Problems als ganzzahliges lineares Programm als auch ein Schnittebenenverfahren zu dessen Lösung entwickelten. Mit den neuen Methoden berechneten sie eine Tour für ein konkretes Rundreiseproblem (eine sogenannte Instanz) mit 49 Städten und bewiesen, dass es keine kürzere Tour geben konnte. In den 1960er und 1970er Jahren befassten sich zahlreiche interdisziplinäre Forschergruppen mit der Mathematik des Problems und dessen Anwendungen u. a. in der Informatik, den Wirtschaftswissenschaften, der Chemie und der Biologie.

Richard M. Karp bewies im Jahre 1972 die NP-Vollständigkeit des Hamiltonkreisproblems, aus der sich leicht die NP-Äquivalenz des TSP ableiten lässt. Damit lieferte er eine theoretische Begründung für die schwere Lösbarkeit dieses Problems in der Praxis.

Größere Fortschritte darin wurden Ende der 1970er und 1980er Jahren erzielt, als es Martin Grötschel, Manfred Padberg, Giovanni Rinaldi und anderen gelang, mit Hilfe von neuen Schnittebenen und einem Branch-and-Cut-Verfahren einige Probleminstanzen mit bis zu 2392 Städten optimal zu lösen.

In den 1990er Jahren begannen David Applegate, Robert Bixby, Vašek Chvátal und William Cook mit der Entwicklung des Programms Concorde, das an sämtlichen Lösungsrekorden der letzten Jahre beteiligt war. Gerhard Reinelt stellte 1991 die TSPLIB bereit, eine Sammlung standardisierter Testinstanzen mit unterschiedlichem Schwierigkeitsgrad, anhand derer verschiedene Forschergruppen ihre Resultate vergleichen konnten. Im Jahre 2005 berechnete Cook in Zusammenarbeit mit anderen eine beweisbar kürzeste Tour durch die 33.810 Städte eines Layoutproblems für integrierte Schaltkreise, was die bislang größte optimal gelöste TSPLIB-Instanz ist. Für andere Instanzen mit mehreren Millionen Städten konnten sie mit Hilfe zusätzlicher Dekompositionstechniken Touren bestimmen, deren Länge beweisbar weniger als 1 % vom Optimum entfernt liegt.

Mathematische Beschreibung

Modellierung als Graph

Symmetrisches TSP auf vier Städten

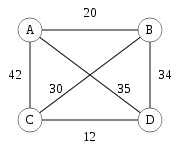
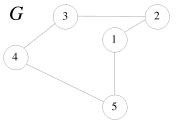
Damit mathematische Verfahren zur Lösung verwendet werden können, muss eine reale Situation zunächst durch ein einfaches Modell abgebildet werden. Das Problem des Handlungsreisenden lässt sich mit Hilfe eines Graphen modellieren, das heißt: durch Knoten und Kanten. Dabei repräsentieren die Knoten (im Bild: A bis D) die Städte, während jede Kante (i,j) zwischen zwei Knoten i und j eine Verbindung zwischen diesen Städten beschreibt. Zu jeder Kante (i,j) gibt es eine Länge 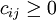$c_{ij} \geq 0$ (im Bild: 20, 42,...), die sich je nach Zusammenhang beispielsweise als geographische Länge einer Verbindung, als Reisezeit oder als Kosten einer Reise zwischen zwei Städten interpretieren lässt. Eine Tour (auch Hamiltonkreis genannt) ist ein Kreis in diesem Graphen, der jeden Knoten genau einmal enthält. Ziel ist es, eine möglichst kurze Tour zu finden.

Um die Untersuchung des Problems zu vereinfachen und um sicherzustellen, dass es eine Tour gibt, wird meist angenommen, dass der Graph vollständig ist, dass also zwischen je zwei Knoten immer eine Kante existiert. Dies lässt sich dadurch erreichen, dass überall dort, wo keine Kante existiert, eine künstliche, sehr lange Kante eingefügt wird. Aufgrund ihrer hohen Länge wird eine solche Kante nie in einer kürzesten Tour vorkommen, es sei denn, es gäbe sonst keine Tour.

Je nach Eigenschaften der Kantengewichte werden noch unterschiedliche Spezialfälle des Problems unterschieden, von denen die wichtigsten das symmetrische und das metrische TSP sind.

Asymmetrisches und symmetrisches TSP

Beim allgemeinen asymmetrischen TSP können die Kanten in Hin- und Rückrichtung unterschiedliche Länge haben, so dass dieses Problem mit Hilfe eines gerichteten Graphen modelliert werden muss. Es reicht also nicht, bloß von der Verbindung zwischen zwei Knoten und ihrer Länge zu sprechen; zusätzlich muss noch die Richtung angegeben werden.

Beim symmetrischen TSP dagegen sind für alle Knotenpaare (i,j) die Kantenlängen in beide Richtungen identisch, d. h. es gilt c_ij = c_ji. Als Konsequenz davon hat jede Tour in beide Richtungen dieselbe Länge. Die Symmetrie halbiert also die Anzahl der möglichen Touren. Ein symmetrisches TSP wird üblicherweise mit Hilfe eines ungerichteten Graphen modelliert (wie im Bild). Ein Traveling Salesman Problem zwischen realen Städten kann asymmetrisch oder symmetrisch sein, je nachdem, ob beispielsweise durch Baustellen oder Einbahnstraßen der Weg in eine Richtung länger dauert als in die andere oder nicht. Ebenso könnte die Reise zu Wasser oder in der Luft unterschiedlichen (Luft-)Strömungen ausgesetzt sein.

Metrisches TSP

Ein symmetrisches TSP heißt metrisch, wenn zusätzlich seine Kantenlängen die Dreiecksungleichung erfüllen. Anschaulich bedeutet dies, dass sich Umwege nicht lohnen, weil die direkte Verbindung von i nach j nie länger ist als der Weg von i nach j über einen dritten Knoten k:

$c_{ij} \le c_{ik} + c_{kj}$

Solche Kantenlängen definieren eine Metrik auf der Knotenmenge, also ein Entfernungsmaß, das die intuitiv von einem Abstand erwarteten Bedingungen erfüllt. Mehrere in der Praxis häufig auftretende Distanzfunktionen sind Metriken, erfüllen also die Dreiecksungleichung:

• die euklidische Metrik des euklidischen TSP,
• die Manhattan-Metrik (auch City-Block-Metrik) des rektilinearen TSP, bei der die Distanz zwischen zwei Knoten eines gitterförmigen Graphen (wie dem Straßennetz von Manhattan) die Summe der Entfernungen in x- und y-Richtung ist,
• oder die Maximums-Metrik, bei der die Distanz zwischen zwei Knoten eines gitterförmigen Graphen das Maximum der Entfernungen in x- bzw. y-Richtung ist.

Die letzten beiden Metriken finden beispielsweise Anwendung beim Bohren von Leiterplatten, wo ein Bohrer, der eine vorgegebene Menge von Löchern in möglichst kurzer Zeit abarbeiten muss, in beide Dimensionen unabhängig bewegt werden kann, um von einem Loch zum nächsten zu gelangen. Die Manhattan-Metrik entspricht dem Fall, dass die Bewegung in beide Richtungen nacheinander erfolgt, während bei der Maximum-Metrik beide Bewegungen gleichzeitig erfolgen und die Gesamtzeit von der jeweils längeren Strecke in x- bzw. y-Richtung bestimmt wird.

Ein nicht-metrisches TSP kann zum Beispiel vorliegen, wenn die Dauer einer Reise minimiert werden soll und auf verschiedenen Strecken verschiedene Verkehrsmittel möglich sind. Dabei kann ein Umweg mit dem Flugzeug schneller sein als die direkte Verbindung mit dem Auto.

Falls es im praktischen Planungsproblem zulässig ist, Orte mehrfach zu besuchen, lässt sich das symmetrische TSP auf das metrische TSP reduzieren. Dazu wird das Rundreiseproblem auf dem sogenannten Distanzgraphen betrachtet. Dieser hat dieselbe Knotenmenge wie der ursprüngliche Graph und ist ebenfalls vollständig. Die Kantenlängen c_ij zwischen zwei Knoten i und j im Distanzgraphen entsprechen der Länge eines kürzesten i − j − Weges zwischen diesen Knoten im ursprünglichen Graphen. Die so definierten Werte c_ij erfüllen immer die Dreiecksungleichung, und jede Tour im Distanzgraphen entspricht einer Tour mit möglichen Knotenwiederholungen im ursprünglichen Graphen.

Formulierung als ganzzahliges lineares Programm

Ein Ansatz zur Lösung des Problems ist die Formulierung als ganzzahliges lineares Programm, in dem die Entscheidungen durch Variablen und die Bedingungen durch lineare Ungleichungen beschrieben werden. Hierfür gibt es mehrere mögliche Varianten. Beispielhaft soll hier eine Modellierung für das symmetrische TSP mit Knotenmenge V vorgestellt werden. Für jede Kante {i,j} wird eine binäre Variable 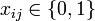$x_{ij} \in \{0,1\}$ eingeführt, die für eine gegebene Tour angibt, ob die Kante {i,j} in dieser Tour enthalten ist (x_ij = 1) oder nicht (x_ij = 0). Jede Tour lässt sich auf diese Art durch Angabe der zugehörigen Variablenwerte angeben, aber nicht jede 0-1-Belegung der Variablenwerte definiert eine Tour. Die Bedingungen dafür, dass eine Variablenbelegung eine Tour definiert, lassen sich durch lineare Ungleichungen ausdrücken, die im folgenden vorgestellt werden sollen.

Gradbedingung: In jeden Knoten i muss genau eine Kante der Tour hinein- bzw. hinausgehen.

Jeder Knoten muss über genau zwei Tourkanten mit den restlichen Knoten verbunden sein, nämlich durch eine hinein- und eine hinausführende Kante:

$\sum_{j \in V \setminus \{i\}} x_{ij} = 2 \qquad (1)$

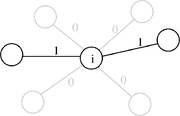
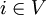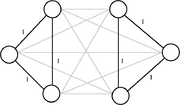
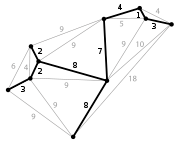
für alle $i \in V$. In der Summe ist jeder Summand x_ij entweder 1 (in der Tour enthalten) oder 0 (nicht enthalten). Die Summe zählt daher genau die Zahl der Kanten der Tour, die den Knoten i als Endknoten haben. Sie muss den Wert 2 annehmen, da jeweils eine Kante hinein- und hinausführen muss. Im nebenstehenden Bild ist ein Knoten i mit ein- und ausgehenden Kanten dargestellt, wobei die Tourkanten fett gekennzeichnet sind. An den Kanten stehen die Werte x_ij, die zu den oben genannten Summen beitragen.

Kurzzyklen: Diese Variablenbelegung erfüllt alle Gradbedingungen, definiert aber keine Tour.

Die obigen Gradbedingungen werden nicht nur von Touren erfüllt, sondern auch von Variablenbelegungen, die mehrere getrennte Kreise (sogenannte Kurzzyklen) beschreiben, wobei jeder Knoten in genau einem Kreis enthalten ist (siehe Bild). Um so etwas auszuschließen, müssen noch Kurzzyklusungleichungen (auch Subtour-Eliminationsbedingungen genannt) erfüllt werden. Diese von Dantzig, Fulkerson und Johnson 1954 als loop conditions eingeführten Nebenbedingungen besagen, dass jede Knotenmenge 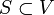$S \subset V$, die weder leer ist noch alle Knoten enthält, durch mindestens zwei Kanten der Tour mit den restlichen Knoten verbunden sein muss:

$\sum_{i \in S, \; j \notin S} x_{ij} \geq 2 \qquad (2)$

für alle Knotenmengen S mit 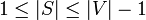$1 \leq |S| \leq |V|-1$. Die Summe zählt alle Kanten der Tour zwischen einem Knoten 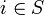$i \in S$ und einem anderen Knoten 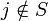$j \notin S$. Zur Vermeidung redundanter Ungleichungen kann man sich auch auf Knotenmengen S mit mindestens zwei und höchstens | V | − 2 Knoten beschränken. Im nebenstehenden Bild sind wieder die Kanten {i,j} mit x_ij = 1 fett gezeichnet, während die übrigen Kanten den Wert x_ij = 0 haben. Das Hinzufügen der Bedingung (2) für die Knotenmenge S, die aus den drei linken Knoten besteht, würde dafür sorgen, dass S durch mindestens zwei Tourkanten mit den drei rechten Knoten verbunden sein muss, und damit die beiden gezeigten Kurzzyklen ausschließen. Die Anzahl der Subtour-Eliminationsbedingungen nach Dantzig, Fulkerson und Johnson beträgt 2ⁿ − 2(n − 1). Eine 1960 von Miller, Tucker und Zemlin veröffentlichte alternative Darstellung der Nebenbedingungen zur Vermeidung von Subtouren kommt durch Einführung von n neuen Variablen, die die Reihenfolge der besuchten Orte angeben, mit nur n² − n + 1 Nebenbedingungen aus. Allerdings bleibt das TSP wegen der Binarität der x_ij auch mit der Formulierung nach Miller, Tucker und Zemlin weiterhin NP-schwer.

Da jeder Vektor 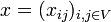$x=(x_{ij})_{i,j \in V}$ mit Einträgen aus 0 und 1, der alle diese Ungleichungen erfüllt, eine gültige Rundreise definiert, ergibt sich als reformuliertes Problem des Handlungsreisenden: Finde

$\min \; \left\{ \sum_{i \in V} \sum_{j \in V \setminus \{i\}} c_{ij} x_{ij} \;|\; x \mbox{ erf}\rm{{\ddot u}}\mbox{llt (1) und (2) }, \; x_{ij} \in \{0,1\} \right\}. \qquad (3)$

Da die Variablen x_ij nur die Werte 0 oder 1 annehmen, zählt die Summe genau die Längen c_ij der Kanten {i,j} zusammen, die in der Tour enthalten sind.

Die Zahl der Ungleichungen vom Typ (2) wächst exponentiell mit der Anzahl der Städte, da fast jede der 2 ^{| V |} Teilmengen von Knoten eine Ungleichung definiert. Dieses Problem kann aber mit Hilfe von Schnittebenenverfahren umgangen werden, bei denen diese Ungleichungen erst dann hinzugefügt werden, wenn sie tatsächlich gebraucht werden. Geometrisch lässt sich jede lineare Ungleichung als Hyperebene im Raum der Variablen interpretieren. Die Menge der zulässigen Lösungen bildet in diesem Raum ein Polytop, also ein mehrdimensionales Vieleck, dessen genaue Gestalt von den Kosten c_ij abhängt und meist unbekannt ist. Man kann aber zeigen, dass die meisten der Bedingungen (1) und (2) Facetten des TSP-Polytops definieren, also Seitenflächen des Polytops mit höchstmöglicher Dimension. Damit gehören sie zu den stärksten linearen Ungleichungen, die es zur Beschreibung einer Tour geben kann. Es gibt noch viele weitere Facetten, deren zugehörige Ungleichungen allerdings nur in wenigen Fällen bekannt sind. Obwohl (1) und (2) zusammen mit der Beschränkung auf 0/1-Vektoren das Problem vollständig modellieren, können solche zusätzlichen Ungleichungen innerhalb eines Branch-and-Cut-Verfahrens zur Formulierung hinzugefügt werden, um bestimmte LP-Lösungen mit nicht-ganzzahligen Koordinaten auszuschließen (siehe Abschnitt Exakte Lösungsverfahren).

Algorithmische Komplexität

Da dem Handlungsreisenden in jedem Schritt die Städte zur Auswahl stehen, die er noch nicht besucht hat, gibt es (n-1)! mögliche Touren für ein asymmetrisches und (n − 1)! / 2 Touren für ein symmetrisches TSP. Die Größe des Suchraums hängt also überexponentiell von der Anzahl der Städte ab.

Das Problem des Handlungsreisenden ist sowohl für den allgemeinen als auch für den symmetrischen oder metrischen Fall NP-äquivalent. Unter der allgemein vermuteten, bisher aber unbewiesenen Annahme, dass die Komplexitätsklassen P und NP verschieden sind (siehe P-NP-Problem), folgt daraus, dass keine deterministische Turingmaschine existiert, die das Problem für jede Instanz in polynomialer Laufzeit bezüglich der Anzahl der Städte löst.

Ferner ist bekannt, dass es unter der Annahme P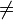$\neq$NP für das allgemeine Problem des Handlungsreisenden keinen Polynomialzeitalgorithmus geben kann, der für irgendein Polynom p grundsätzlich eine Lösung berechnet, deren Wert höchstens um einen Faktor 2^p(n) vom Optimalwert abweicht.

Allerdings lassen sich für das metrische TSP Approximationsalgorithmen angeben, die in polynomieller Laufzeit eine Lösung liefern, die höchstens doppelt (Minimum-Spanning-Tree-Ansatz) bzw. höchstens 1,5 mal (Algorithmus von Christofides) so lang wie die optimale Lösung ist (siehe unten). Bisher ist kein Polynomialzeitalgorithmus mit einer besseren Gütegarantie als 1,5 bekannt. Unter der Annahme P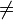$\neq$NP gibt es eine (unbekannte) Konstante c > 0, so dass kein Polynomialzeitalgorithmus für das metrische TSP existieren kann, der die Güte 1 + c garantiert. Arora hat gezeigt, dass für das euklidische TSP ein polynomiales Approximationsschema (PTAS) existiert.

Lösungsverfahren

Die bekannten Lösungsverfahren unterteilen sich in zwei Gruppen, die miteinander kombiniert werden können. Exakte Lösungsverfahren finden – beliebig lange Laufzeit vorausgesetzt – grundsätzlich eine beweisbare Optimallösung. Heuristische Verfahren finden oft in kurzer Zeit gute Lösungen, die aber im allgemeinen Fall beliebig schlecht sein können. Für das metrische TSP gibt es polynomiale Heuristiken, deren Lösungen grundsätzlich höchstens um den Faktor 1,5 bzw. 2 länger sind als eine kürzeste Rundreise.

Exakte Lösungsverfahren

Hauptartikel: Branch-and-Cut

Das Problem des Handlungsreisenden kann exakt gelöst werden, indem man die Weglängen aller möglichen Rundreisen berechnet und dann eine mit der kleinsten Weglänge auswählt. Das ist aber schon bei einer kleinen Zahl von Städten nicht mehr praktisch durchführbar. Bei der einfachsten Variante, dem symmetrischen TSP mit n Städten, gibt es (n − 1)! / 2 verschiedene Rundreisen, das sind bei 15 Städten über 43 Milliarden und bei 18 Städten bereits über 177 Billionen. Wie schnell die Rechenzeit mit wachsender Anzahl von Städten wächst zeigt das folgende Beispiel. Hat man einen Rechner, der die Lösung für 30 Städte in einer Stunde berechnet, dann braucht dieser für zwei zusätzliche Städte annähernd die tausendfache Zeit; das sind mehr als 40 Tage.

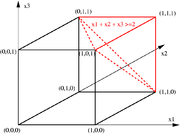TSP auf drei Knoten: Die rot gestrichelte Schnittebene 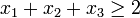$x_1 + x_2 + x_3 \geq 2$ schneidet alle unzulässigen Lösungen mit höchstens einer Kante ab. Alle Punkte im roten Polytop erfüllen diese Ungleichung, u. a. der einzige zulässige Punkt (1,1,1).

Mit Methoden der ganzzahligen linearen Optimierung, insbesondere Branch-and-Cut, lassen sich dagegen Instanzen in praktisch relevanten Größenordnungen beweisbar optimal lösen, oder zumindest die Güte einer gefundenen Tour im Vergleich zu einer Optimallösung abschätzen. Geometrisch interpretiert, betrachten diese Verfahren das Problem als konvexes Polytop, also als mehrdimensionales Vieleck, im m-dimensionalen Einheitswürfel [0,1]^m, wobei m die Anzahl der Kanten des Graphen ist. Jede Ecke dieses Einheitswürfels beschreibt eine Tour, sofern der zugehörige 0/1-Vektor die oben beschriebenen linearen Ungleichungen erfüllt. Die zu diesen Ungleichungen gehörenden Hyperebenen schneiden daher Ecken des Einheitswürfels ab, die keine Tour darstellen.

Das nebenstehende Bild illustriert dies für das (sehr einfache) TSP mit drei Knoten. Entsprechend den drei möglichen Kanten zwischen diesen Knoten gibt es auch drei binäre Variablen 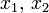$x_1,\, x_2$ und x₃. Es gibt in diesem Fall nur eine mögliche Tour, nämlich diejenige, die alle drei Kanten benutzt. Diese Tour erfüllt die Ungleichung 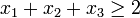$x_1 + x_2 + x_3 \geq 2$, die besagt, dass jede Tour mindestens zwei Kanten haben muss. Außer dieser Tour, die dem Punkt (1,1,1) entspricht, erfüllen auch alle Punkte im rot eingegrenzten Bereich diese Ungleichung. Die zugehörige Schnittebene, die durch die rot gestrichelten Linien aufgespannt wird, schneidet also alle Ecken ab, die unmöglichen Touren mit höchstens einer Kante entsprechen, nämlich den Nullvektor (0,0,0) und die Einheitsvektoren (1,0,0), (0,1,0) und (0,0,1). Die stärkere Ungleichung 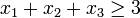$x_1 + x_2 + x_3 \geq 3$ würde alles vom Einheitswürfel abschneiden außer dem einzigen zulässigen Punkt (1,1,1). In diesem speziellen Fall lässt sich derselbe Effekt auch schon durch die drei Ungleichungen vom Typ (1) erzielen.

Durch Lösen vieler linearer Programme, Abschneiden nicht benötigter Teile des Einheitswürfels mit Hilfe weiterer Schnittebenen (z. B. vom Typ (2), oder auch Kamm-, Cliquenbaum- und Domino-Parity-Ungleichungen^[1]) sowie durch Aufteilung in mehrere Teilpolytope mit Hilfe von Branch-and-Bound wird versucht, eine zulässige 0/1-Ecke mit minimalem Zielfunktionswert zu bestimmen. Eine genauere Beschreibung dieser Verfahren ist im Artikel Ganzzahlige lineare Optimierung zu finden.

Die alleinige Anwendung dieser Verfahren reicht meist nicht aus, um schnell gute Rundreisen zu finden. Ihr Hauptvorteil liegt darin, dass sie Angaben liefern, wie lang eine kürzeste Tour mindestens sein muss. Mit einer solchen unteren Schranke für den optimalen Lösungswert lässt sich abschätzen, wie gut eine gefundene Tour im Vergleich zu einer optimalen Rundreise ist, ohne diese zu kennen. Hat man beispielsweise eine untere Schranke von 100 und eine Tour der Länge 102 gefunden, kann eine optimale Tour nur zwischen 100 und 102 liegen. Die so genannte Optimalitätslücke, also der maximale relative Abstand zwischen der optimalen Tourlänge und der kürzesten bekannten Tourlänge, beträgt daher (102-100)/100 = 2 %, d. h; der gefundene Lösungswert 102 ist höchstens 2 % vom Optimalwert entfernt. Wenn die Länge einer gefundenen Tour genauso groß ist wie die untere Schranke, ist damit bewiesen, dass die gefundene Lösung optimal ist. Um gute Touren zu finden, können diese exakten Verfahren mit Heuristiken kombiniert werden, von denen einige im nachfolgenden Abschnitt beschrieben werden.

Heuristiken

Um schnell zu brauchbaren Lösungen zu kommen, sind meist durch Heuristiken motivierte Näherungsverfahren notwendig, die aber in der Regel keine Güteabschätzung für die gefundenen Lösungen liefern. Je nachdem, ob eine Heuristik eine neue Tour konstruiert oder ob sie versucht, eine bestehende Rundreise zu verbessern, wird sie als Eröffnungs- (auch Konstruktions-) oder Verbesserungsverfahren bezeichnet. Darüber hinaus gibt es Dualheuristiken, die Mindestlängen für eine Tour berechnen. Metaheuristiken können mehrere dieser Einzelheuristiken unterschiedlich kombinieren. Eine Übersicht über die meisten der hier vorgestellten Heuristiken ist im Abschnitt Übersicht zu finden.

Eröffnungsverfahren

Die Nearest-Neighbor-Heuristik besucht in jedem Schritt den nächstgelegenen Knoten.

Dem intuitiven Vorgehen eines Handlungsreisenden entspricht wohl am ehesten die Nearest-Neighbor-Heuristik (nächster Nachbar). Von einer Stadt ausgehend wählt diese jeweils die nächstgelegene als folgenden Ort aus. Dieses wird sukzessive fortgesetzt, bis alle Städte bereist wurden und der Handlungsreisende zum Ausgangsort zurückgekehrt ist. Die hiermit verwandte Farthest-Neighbor-Heuristik besucht in jedem Schritt die am weitesten entfernt liegende Stadt. In jeder Stadt muss also der kürzeste bzw. weiteste ausgehende Weg gesucht werden. Maximal kann es pro Stadt nur so viele ausgehende Kanten geben, wie Knoten im Graphen vorhanden sind. Daraus ergibt sich eine algorithmische Komplexität von O(n²), die Anzahl der Rechenschritte hängt also quadratisch von der Zahl der Städte ab. Dass diese Heuristik im Allgemeinen jedoch nicht die beste Lösung liefert, liegt daran, dass die Distanz zwischen der Ausgangsstadt und der letzten besuchten Stadt bis zuletzt nicht berücksichtigt wird. Die Nearest- und die Farthest-Neighbor-Heuristik können beliebig schlechte Ergebnisse liefern, das heißt, es gibt keinen konstanten, instanzunabhängigen Approximationsfaktor für den Lösungswert im Vergleich zum Optimalwert.

Eine ganze Klasse weiterer Eröffnungsverfahren bilden die sogenannten Einfüge-Heuristiken. Die einfachsten Varianten davon sind die Nearest-Insertion-Heuristik (nächste Einfügung) und die Farthest-Insertion-Heuristik (entfernteste Einfügung). Gegeben seien (wenige) einander benachbarte Städte, für die sich durch exakte Verfahren schnell eine optimale Rundreise ermitteln lässt. Nun wird schrittweise überprüft, welche noch nicht besuchte Stadt am nächsten (beziehungsweise am entferntesten) zu einer der Verbindungslinien der bisherigen Rundreise liegt. Ist diese Stadt gefunden, so wird sie zwischen den ihr am nächsten liegenden Städten in die Tour eingebaut. Das Verfahren wird solange fortgesetzt, bis die Rundreise alle Städte umfasst. Auch die Lösungen dieser Heuristik können im Vergleich zu einer Optimallösung beliebig schlecht sein.

Ein minimal aufspannender Baum verbindet alle Punkte eines Graphen bei minimaler Kantenlänge

Eine andere Klasse von Heuristiken unterteilt die Knotenmenge in einzelne Partitionen (z. B. nach geographischen Kriterien), die jeweils teiloptimiert werden. Anschließend werden die Teillösungen zu einer Gesamtlösung kombiniert. Diese ist in der Regel nur lokal optimal und kann gegenüber dem globalen Optimum beliebig schlecht sein.

Die Minimum-Spanning-Tree-Heuristik (MST) berechnet zunächst einen minimal aufspannenden Baum, also einen Graphen, in dem alle Punkte miteinander verbunden sind und der minimale Länge besitzt. Davon ausgehend wird eine Tour konstruiert, indem zunächst alle Baumkanten verdoppelt werden und danach eine „Eulertour“ in dem entstandenen eulerschen Graphen gesucht wird. Diese wird zuletzt durch direkte Kanten abgekürzt, falls Knoten doppelt besucht werden. Im Falle eines metrischen TSP kann man zeigen, dass die so konstruierte Tour höchstens doppelt so lang ist wie eine kürzeste Tour.

Eine noch bessere Approximationsgüte für metrische TSP wird durch die Christofides-Heuristik erreicht. Mit ihr kann eine Rundreise berechnet werden, die höchstens eineinhalb mal so lang wie eine optimale ist. Hierbei wird statt der Verdopplung der Kanten in der MST-Heuristik eine kleinste perfekte Paarung auf den Knoten ungeraden Grades im minimal aufspannenden Baum berechnet, um einen eulerschen Graphen zu erzeugen. Dieser Algorithmus ist jedoch aufwändiger.

Verbesserungsverfahren

Verbessernde Optimierungsverfahren, auch Post-Optimization-Verfahren (Nach-Optimierung) versuchen, eine bestehende Tour durch kleine Modifikationen zu verkürzen. Führt keine der betrachteten Änderungen mehr zu einer Verbesserung, so ist ein lokales Optimum gefunden (aber nicht notwendigerweise ein globales). Die k-Opt-Heuristiken verfolgen diesen Ansatz, indem sie systematisch Gruppen von k Kanten aus der Tour entfernen und durch k andere Kanten ersetzen, so dass wieder eine Tour entsteht. Da eine vollständige Durchführung dieses Verfahrens einer Aufzählung aller möglichen Touren entsprechen würde, ist k in praktischen Implementierungen üblicherweise höchstens 5. Dabei werden oft alle Austauschmöglichkeiten von zwei und drei Kanten durchprobiert, während Kantenaustausche von mehr als drei Kanten wegen des Rechenaufwandes nur noch sehr sparsam eingesetzt werden.

Die Güte einer k-Opt-Heuristik in der Praxis hängt stark von der Auswahl der auszutauschenden Kanten und des Parameters k ab, für die es verschiedene heuristische Kriterien gibt. Eine bekannte k-Opt-basierte Heuristik ist die Lin-Kernighan-Heuristik, die 1973 von S. Lin und B.W. Kernighan entwickelt wurde und in der Implementierung von Keld Helsgaun^[2] unter anderem an der optimalen Lösung des TSP durch 24.978 schwedische Städte im Jahre 2004 beteiligt war. Sie basiert darauf, erst alle Austauschmöglichkeiten von zwei Kanten durchzutesten, dann solche mit drei Kanten, usw., bis eins von mehreren möglichen Abbruchkriterien erfüllt ist.

Metaheuristische Verfahren

Metaheuristiken kombinieren lokale und globale Suchverfahren in einer abstrakten Strategie für die heuristische Optimierung eines Problems. Viele dieser Verfahren basieren auf lokaler Suche, d. h. sie berechnen eine heuristische Startlösung (beispielsweise mit der Nearest-Neighbor-Heuristik) und verbessern diese solange durch ein lokales Suchverfahren, wie z. B. K-Opt-Heuristiken, bis keine bessere Tour mehr gefunden wird. Durch verschiedene Strategien, wie beispielsweise Tabu-Suche oder Simulierte Abkühlung, kann versucht werden, das Steckenbleiben in lokalen Minima weitestgehend zu verhindern. Andere Ansätze, wie Ameisenalgorithmen, genetische Algorithmen oder künstliche neuronale Netze (dort vor allem das Hopfield-Netz), haben natürliche Prozesse als Vorbild. Prinzipiell können all diese Verfahren gute Lösungen berechnen, aber auch beliebig schlecht im Vergleich zu einer Optimallösung sein. Ihre Qualität und Laufzeit hängen wesentlich von der Definition und Implementierung der einzelnen Schritte ab.

Duale Heuristiken

Das Problem des Handlungsreisenden ist eines der wenigen kombinatorischen Optimierungsprobleme, bei dem sich auf einfache Weise brauchbare untere Schranken für die minimale Länge einer Tour (allgemein: die minimalen Kosten einer Lösung) angeben lassen. Diese Schranken sind insbesondere wichtig um Aussagen über die Güte einer zulässigen Tour zu treffen. Da beispielsweise jede Tour, also insbesondere auch eine optimale, genau n Kanten enthält, muss sie mindestens so lang sein wie die Summe der n kleinsten Kantenlängen. Eine andere untere Schranke ergibt sich aus der Beobachtung, dass beim Löschen einer beliebigen Kante aus einer Tour ein aufspannender Baum entsteht, also ein Teilgraph, der alle Knoten, aber keine Kreise enthält. Die Tour ist mindestens so lang wie dieser Baum und damit per Definition auch mindestens so lang wie ein minimal aufspannender Baum (also ein aufspannender Baum mit minimaler Summe der Kantenlängen), der sich leicht bestimmen lässt. Da dies für jede Tour gilt, liefert die Länge eines minimal aufspannenden Baums eine untere Schranke für die Länge einer optimalen Tour. Etwas allgemeiner kann man auch einen sogenannten minimalen 1-Baum berechnen. Dies ist ein minimal aufspannender Baum zwischen den Knoten 2 bis n (bei beliebiger Nummerierung), der über die zwei kürzestmöglichen Kanten an den Knoten mit der Nummer 1 angebunden wird (daher der Name). Auch dessen Länge liefert eine untere Schranke. Weiterhin ist jede Tour auch ein perfektes 2-Matching. Das bedeutet also, dass eine kürzeste Tour mindestens so lang sein muss, wie der Wert eines minimalen perfekten 2-Matchings, das sich in O(n³) berechnen lässt.

Übersicht

In der folgenden Übersichtstabelle sind für die meisten hier vorgestellten Heuristiken der Typ des Verfahrens, die maximale Laufzeit bei n Städten sowie evtl. Gütegarantien für die berechneten Lösungen aufgeführt. Da die Laufzeit und Qualität von Metaheuristiken stark von der Wahl der Teilalgorithmen abhängig sind und sich nicht allgemein angeben lassen, sind sie hier nicht aufgeführt.

Verfahren	Typ	Laufzeit	Max. Abweichung vom Optimum
Nearest-/Farthest-Neighbor-Heuristik	Eröffnungsheuristik	O(n²)	beliebig groß
Nearest-/Farthest-Insertion-Heuristik	Eröffnungsheuristik	O(n²)	beliebig groß
Minimum-Spanning-Tree-Heuristik	Eröffnungsheuristik	O(n² log n)	Faktor 2 (metrisches TSP)
Christofides-Heuristik	Eröffnungsheuristik	O(n³)	Faktor 1,5 (metrisches TSP)
K-Opt-Heuristik	Verbesserungsheuristik	O(k!) pro Schritt	beliebig groß
Summe der n kürzesten Kanten	Dualheuristik	O(n² log n)	beliebig groß
Länge eines minimalen aufspannenden Baumes	Dualheuristik	O(n² log n)	beliebig groß

Praktische Grenzen der Berechenbarkeit

Die größte Instanz eines (symmetrischen) Rundreiseproblems, die bisher nachweisbar optimal gelöst wurde, ist ein Planungsproblem für das Layout integrierter Schaltkreise mit 33.810 Knoten. Dieser Rekord wurde im Jahre 2005 von William Cook und anderen mit Hilfe einer Kombination aus verschiedenen Heuristiken und dem Branch-and-Cut-basierten Programm Concorde aufgestellt, wobei frühere Teilergebnisse verschiedener universitärer Arbeitsgruppen als Grundlage verwendet wurden^[1]. Die bis dahin größte optimal gelöste Instanz bestand aus 24.978 schwedischen Städten, gelöst im Jahre 2004. Mit Hilfe spezieller Dekompositionstechniken und dem Einsatz mehrerer paralleler Computer haben William Cook u. a. Touren für ein TSP auf über 526 Millionen Sternen gefunden, deren Länge nachweislich höchstens 0,798 % vom Optimum abweicht.

Aus der Tatsache, dass ein TSP einer bestimmten Größe optimal gelöst werden konnte, folgt jedoch nicht, dass jede Instanz dieser Größe optimal gelöst werden kann, da – wie bei den meisten kombinatorischen Optimierungsproblemen – die Schwierigkeit der Lösung stark von den Eingabeparametern (in diesem Fall den Kantengewichten) abhängt. Ein kleineres Problem kann deutlich schwerer lösbar sein; beispielsweise gibt es in der TSPLIB eine aufgrund ihrer vielen Symmetrien schwer optimal zu lösende Instanz mit nur 225 Städten^[3]. Bei TSPs, die aus praktischen Anwendungen entstehen, müssen oft noch weitere Nebenbedingungen, wie beispielsweise Zeitfenster, berücksichtigt werden. Daher sind in der Regel die größten optimal lösbaren Probleminstanzen solcher Varianten deutlich kleiner als beim klassischen Problem des Handlungsreisenden, so dass in der Praxis oft auf heuristische Ansätze zur Lösung zurückgegriffen wird. Kombinationen von heuristischen Verfahren mit LP-basierten Verfahren wie Branch-and-Cut werden vor allem im Forschungsumfeld eingesetzt, um mit Hilfe unterer Schranken für die Tourlänge die Qualität von Lösungen und Lösungsverfahren beurteilen zu können.

Varianten und Anwendungen

Schon die in den vorhergehenden Abschnitten beschriebene klassische Variante des Problems tritt in vielen Anwendungen auf, beispielsweise in der DNA-Sequenzierung, beim Layout integrierter Schaltkreise oder bei der Steuerung eines Bohrers in der Herstellung von Leiterplatten^[4]. Darüber hinaus hat sich aus der Praxis heraus eine nahezu unerschöpfliche Auswahl an beliebig kombinierbaren Varianten entwickelt, die zusammen die Familie der TSP bilden und alle NP-schwer sind. Einige dieser Verallgemeinerungen betrachten mehrere Handlungsreisende, während sich andere Varianten durch die grundlegende Veränderung des Optimierungskriteriums oder durch zusätzliche Nebenbedingungen von der klassischen Version unterscheiden.

Die Vorgehensweise in der Praxis unterscheidet sich von der mathematischen Theorie dadurch, dass in der Regel nicht nach einer optimalen Lösung gesucht wird, sondern nur nach einer ausreichend guten. Denn schließlich muss der Gesamtaufwand betrachtet werden, also der Aufwand für Durchführung und Berechnung. Was dabei „gut“ bedeutet und welche Kriterien zum Tragen kommen, hängt dann sehr vom Kontext des Problems ab. So wird man sich für eine einmalige Liefertour weniger Mühe machen als für die Bestückungsplanung einer Leiterplatte, die in einer Millionenauflage hergestellt wird.

Mehrere Handlungsreisende

Beim multiple TSP (mTSP) werden die Städte auf mehrere Handlungsreisende aufgeteilt, wobei alle ihre Rundreisen in derselben Stadt starten und ihre Rundreise dort auch wieder beenden. Jede Stadt muss von genau einem Handlungsreisenden besucht werden. Ziel ist die Minimierung der zurückgelegten Gesamtstrecke. In der Variante mTSP with nonlazy Salesmen werden nur Rundreisen mit mindestens zwei Städten zugelassen, so dass sich jeder Rundreisende tatsächlich fortbewegen muss. Die klassische Version ergibt sich als Spezialfall mit nur einem Handlungsreisenden.

Das Vehicle Routing Problem (VRP) ist ein multiple TSP mit zusätzlichen Kapazitäten. Es entstand direkt aus der praktischen Notwendigkeit der Tourenplanung, bei der Waren aus einem zentralen Depot an Kunden ausgeliefert werden sollen. Die Rundreisen entsprechen den Touren von Transportern mit beschränkter Transportkapazität, die von dem gemeinsamen Depot aus starten und wieder dorthin zurückkehren. Ziel des VRP ist es, alle Kunden möglichst kostengünstig zu beliefern. Dabei kann ein Kunde zwar mehrfach, aber jeweils nur von einem Transporter beliefert werden. In dem Spezialfall, dass die Kapazitäten der Transporter größer sind als die Summe aller Bestellmengen sind, entspricht das VRP dem mTSP und ist daher ebenfalls NP-schwer. Vom Vehicle Routing Problem (VRP) abgeleitete Varianten sind:

• Capacitated VRP (CVRP): Alle Transporter haben die gleiche Kapazität.
• Multiple Depot VRP (MDVRP): Die Transporter können von mehreren verschiedenen Depots starten.
• VRP with Time Windows (VRPTW): Die Kunden können jeweils nur innerhalb vorgegebener Zeitfenster beliefert werden.
• Periodisches VRP (PVRP): Der Bedarf der Kunden wächst in zeitlichen Abständen nach. Betrachtet wird eine bestimmte Zeitdauer.
• Split Delivery VRP (SDVRP): Ein Kunde kann von verschiedenen Transportern beliefert werden.
• VRP with Backhauls (VRPB): Lieferanten und deren Abgabemengen werden berücksichtigt.
• Dynamisches VRP (DVRP): Zusätzlicher Bedarf kann während der Berechnung entstehen, was vorzeitig zu berücksichtigen ist.

Städtecluster

Beim generalized TSP (GTSP) (deutsch: verallgemeinertes TSP) werden mehrere Städte zu einem Cluster zusammengefasst. Der Handlungsreisende muss aus jedem Cluster genau eine Stadt besuchen. Das TSP ist ein Spezialfall des GTSP, in dem jede Stadt in einem Cluster liegt, der eben nur diese eine Stadt enthält. Jede Instanz des GTSP lässt sich in eine Instanz des einfachen TSP überführen und mit den für dieses Problem bekannten Algorithmen lösen. Aus diesem Grund ist auch das GTSP NP-schwer.

In der Praxis werden die Lösungsalgorithmen des GTSP z. B. dazu verwendet, den Leerweg von CNC-Schneidemaschinen zu optimieren. Diese werden unter anderem in der Textilbranche eingesetzt, um aus einer großen Bahn Stoff kleinere Teile für Kleidungsstücke auszuschneiden. Hierbei stellen die auszuschneidenden Konturen die Cluster und die möglichen Ansatzpunkte des Schneidwerkzeuges auf den Konturen die Städte dar.

Änderungen des Optimierungskriteriums

Beim Prize Collecting TSP (PCTSP) werden dem Handlungsreisenden in jeder Stadt bestimmte Preisgelder bezahlt (beispielsweise Verkaufsumsätze). Um von einer Stadt zur nächsten zu reisen, muss er jedoch wiederum Kosten aufbringen. Er soll nun eine vorgegebene Anzahl von Städten und eine Rundreise zwischen diesen Städten so auszuwählen, dass der Gewinn maximal wird. Da das Problem als Spezialfall die klassische Variante enthält (alle Städte müssen besucht werden und alle Preisgelder sind 0), ist das PCTSP ebenfalls NP-schwer. Eine von ihm abgeleitete Spezialform ist das Traveling Salesman Selection Problem (TSSP), bei dem zu vorgegebenem k eine kürzeste Tour zwischen beliebigen k Städten gesucht ist, wobei auf Preisgelder verzichtet wird und metrische Distanzen vorausgesetzt werden.

Beim Bottleneck TSP (BTSP) soll nicht die Summe der Kantenlängen, sondern die Länge der längsten verwendeten Kante minimiert werden. Dies bewirkt eine weniger starke Streuung der einzelnen Distanzen, um möglichen Engpässen, sogenannten Flaschenhälsen, entgegenzuwirken. Eine verwandte Variante ist das maximum scatter TSP, bei dem die kleinste verwendete Länge maximiert wird.

Zusätzliche Nebenbedingungen

Eine in praktischen Anwendungen häufig auftretende zusätzliche Einschränkung sind Zeitfenster, in denen eine Stadt besucht werden muss. Beispielsweise vereinbart ein technischer Kundendienst zur Reparatur von Haushaltsgeräten mit seinen Kunden in der Regel einen Zeitraum, in dem der Besuch des Technikers stattfinden soll. Dieser Zeitraum muss bei der anschließenden Planung der Touren durch den Reparaturbetrieb berücksichtigt werden.

Beim Online TSP sind nicht alle Städte von vornherein gegeben, sondern werden erst nach und nach bekannt, während der Handlungsreisende schon unterwegs ist. Dieser muss dann seine Tour auf Basis der jeweils vorhandenen Daten so planen bzw. abändern, dass neue Städte „möglichst gut“ in seine bisher geplante Tour hineinpassen (was auch immer das in der jeweiligen Anwendung genau bedeutet). Diese Variante tritt beispielsweise bei Pannendiensten wie dem ADAC auf, wo die Positionen liegengebliebener Autos erst nach und nach bekannt werden und die Zentrale versuchen muss, neue Fälle möglichst günstig in die bestehenden Touren der Pannenhelfer einzubauen. Da mehrere von diesen unterwegs sind und die Zentrale bei der Meldung einer Panne auch eine ungefähre Zeitangabe macht, wann ein Pannenhelfer eintreffen wird, handelt es sich hierbei um ein Multiple Online TSP mit Zeitfenstern.

Einzelnachweise

1. ↑ ^{a b} William Cook, Daniel Espinoza, Marcos Goycoolea: Computing with Domino-Parity Inequalities for the TSP. 2005. (Preprint, pdf)
2. ↑ Keld Helsgaun: An Effective Implementation of the Lin-Kernighan Traveling Salesman Heuristic. In: European Journal of Operational Research. Amsterdam 126.2000, Nr. 1, S.106–130. ISSN 0377-2217
3. ↑ TSP-Seite von Vašek Chvátal
4. ↑ Dokumentierte Anwendungen von Concorde

Literatur

• David Applegate, Robert Bixby, Vašek Chvátal, William Cook: On the Solution of Traveling Salesman Problems. Documenta Mathematica. Extraband 3 zum Internationalen Mathematikerkongress. Berlin 1998, S. 645-656. (Postscript)
• David L. Applegate, Robert E. Bixby, Vašek Chvátal, and William J. Cook: The Traveling Salesman Problem. A Computational Study. Princeton University Press, Februar 2007. ISBN 0-691-12993-2
• Lawler, Lenstra, Rinnooy Kan, Shmoys (Hrsg.): The Traveling Salesman Problem. A Guided Tour of Combinatorial Optimization. Wiley, Chichester 1985. ISBN 0-471-90413-9
• W. Domschke: Logistik - Rundreisen und Touren. Oldenbourg-Verlag, München/Wien 1997 (4. Aufl.). ISBN 3-486-29472-5
• T. Grünert, S. Irnich: Optimierung im Transport. Bd 2. Wege und Touren. Shaker Verlag, Aachen 2005. ISBN 3-8322-4515-4

Weblinks

• The Traveling Salesman Problem Home Ausführliche Informationen zum Traveling Salesman Problem (engl.)
• TSPLIB Sammlung von Benchmark-Instanzen des TSP und verschiedener Varianten
• Spektrum der Wissenschaft (4/99): Die optimierte Odyssee Artikel von Martin Grötschel und Manfred Padberg
• The VRP Web Ausführliche Informationen zum Vehicle Routing Problem (engl.)
• 40. Algorithmus der Woche - Informatikjahr 2006 TSP oder die optimale Tour für den Nikolaus